Sonar: Acoustics and the Acoustical Wave Equation
Sonar: Acoustics and the Acoustical Wave Equation
If we were to come up with a tagline for sound, we'd probably say:
- Sound, it's happening all around you. Just like all those plans your friends are making behind your back.
- You can't avoid it. Unless you've got your own personal air shield with a killer password. Then we guess you can…assuming the sound didn't start inside the shield.
- Going out with a bang since…the Big Bang. Or Strings were invented. They can fit any model of universe creation you want, really.
Yeah, maybe those taglines need work, but the point is still there…somewhere. Acoustics, the study of sound, can tell you all about where sound comes from and where it's going.
Although the invention of the first musical instrument isn't set in history books like the invention of plastic or bocce ball, we do know that instruments were around while Aristotle and Pluto were busy philosophizing. Everyone was in the know about instruments turning air into sound by bending it, but it wasn't until the mid to late 1600's that Martin Mersenne and Galileo Galilei established some actual scientific relationships between geometry and physics.
For a while, we didn't have much understanding about how the mechanics related to sound, but Sir Isaac Newton realized it had something to do with pressure. And it all has to do with Newton's Second Law.
Boom.
As a recap, Newton's Second Law tells us that force (F) equals mass times acceleration, which just means that the amount of force something has is the product of its mass and how fast it's gaining speed. If you have the choice of getting hit by two balls gaining speed at the same rate, but one's a foam ball and the other's a bowling ball, which would you rather get hit by?
How about if the foam ball was gaining speed 100 times as quickly as the bowling ball? Newton's Second Law could help you choose in this terrible, terrible ultimatum.
We know, we know, we still haven't mentioned pressure. We're getting there.
Pressure's all about how much stuff is trying to get through how small of a space. The more stuff you have (usually air or liquid), the higher the pressure's going to be. At the same time, the larger the space that stuff's in, the lower the pressure's going to be.
When talking about sound, we're talking about waves that move through air. Air's a bunch of molecules, when you get right down to it. Except, instead of looking at the movement of one single molecule, we're looking at how many molecules move slightly before settling back into place.
Say we have a box full of nine particles. Now we'll add a couple of sound waves. Maybe an "ah," or an "oo." As the molecules move, each particle is being displaced, meaning that they're moving back and forth slightly, but they aren't actually moving with the waves of oohs and ahs.
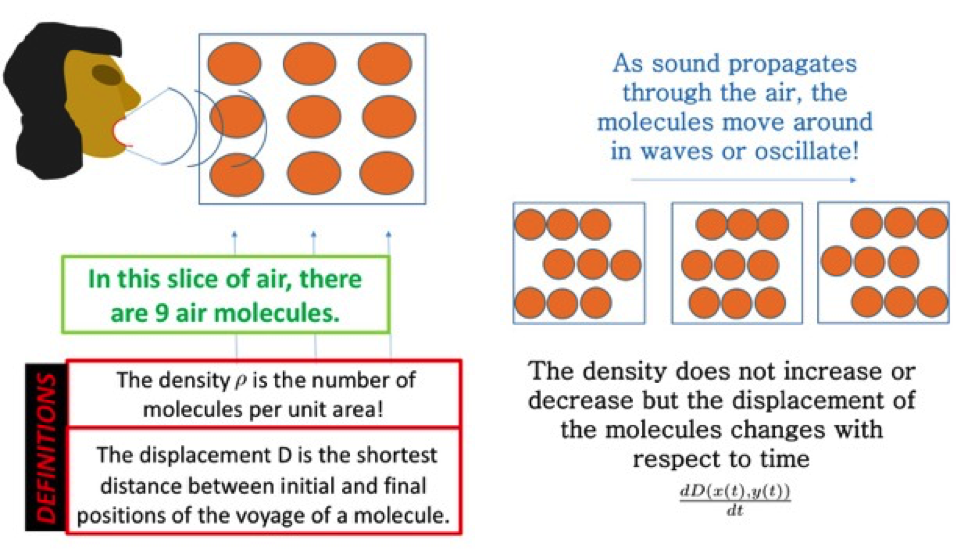
Mass and density can help us figure out just how far away an object can be for the sound to be able to propagate, but only if we know those values.
Once you put those molecules under pressure, everything changes.
When you get right down to it, pressure looks like the following equation, where pressure P equals force, F, divided by area, A, to show how much pressure movement and force create.
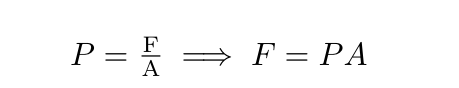
That's a great definition, but it doesn't take into account the fact that waves don't move the molecules, they displace them. We can fix that problem using a little thing called the bulk modulus, and that's going to help a lot in terms of explaining a material's resistance to change.
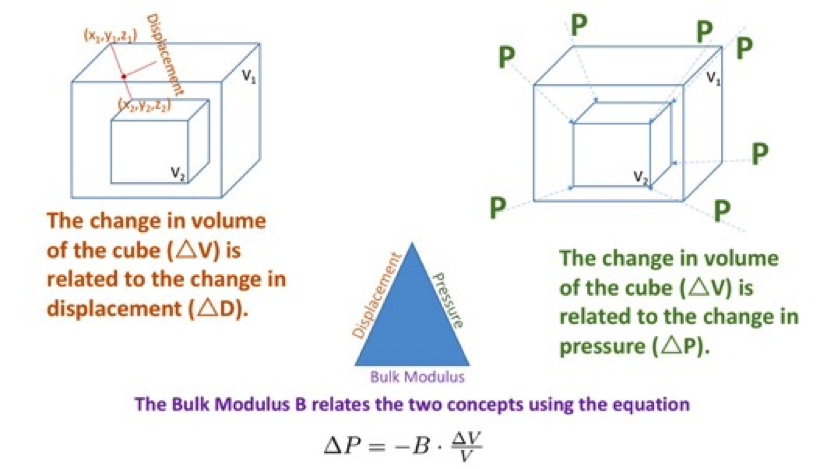
We won't go into the exact details, but the bulk modulus is a handy way of turning the issue of molecules propagating into a table of values depending on the type of material the sound wave is moving through. The bulk modulus handles how displacement works differently depending on the material because that material might be more or less elastic than other materials.
Say you want to send a wave through the air and through the ground. Sending waves through the air's no problem since the molecules are nice and elastic: they have a lot of room to move. The ground is pretty tightly packed, though. It doesn't like moving; it's fairly inelastic. To get a wave to travel through it, that wave's going to need to be really strong.
There's a reason your cousin's recorder recital won't causes tremors the way a subwoofer does. It just doesn't have the power (thank goodness).
(Source)