Sonar: Decibels
Sonar: Decibels
How long can you listen to music before you experience hearing loss?
What? Sorry, we can't hear you; we went to a really loud concert last night and you know the best place to go is right next to the boom if you want to feel the music through your entire body…
Can you actually, truly, really lose your hearing from sitting next to a speaker half the size of your body? Absolutely. Sounds over a certain "loudness" will harm your hearing permanently. You begin to stress out your ears when you overwhelm them with the screech of your favorite band's electric flute for long periods of time.
(That concert was wild. Who knew death metal and flute would be such a great combination?)
Regardless of how "worth it" you think that concert was, your inner ear begins to lose the ability to hear and distinguish certain sound frequencies when you keep the speaker set to 11.
No really; it's true.
All you need to do to figure out how loud is too loud is figure out the number of decibels. The decibel describes sound in human terms: 0 is the softest thing a human can hear. It's also the reason your ears ring the day after that sick flute solo blasted through your ears and into your heart. To find how much is too much, decibels tell us in—wait for it—logarithms. That means every time you add a number to your decibels, you're actually multiplying the intensity of a sound by ten.
Ten!
When it measures things, the decibel gives us an easy way to compare the measurements of large values. If we know the decibel, we can easily see what intensity makes you begin to experience hearing loss.
Let's think about that for a minute. An airplane engine has multiple parts and each one has its own particular sound. The intensity of each component's sound can reach many sound ranges. Sound waves are longitudinal, which means that they propagate (move) through the air by compressing molecules. When all those compressions get moving together, the amount of pressure getting created skyrockets.
And not just because they're rocketing an airplane into the sky.
Those sounds all mix together until you can't figure out which sound is which. In fact, it would even be difficult to find which values would cause hearing loss and which wouldn't. The values are different and all intermingling and there's nothing you can do about it.
Pulling apart the different sounds at their different strengths would be just about impossible without the logarithmic scale. In a logarithmic scale, a single step up in decibels is ten times the intensity. If we base it on numbers that power up that quickly, we don't get bogged down in the little details of which waves are doing what. Instead, we can just add everything together to get a rough estimate of the combined intensity.
Talk about an ear-saver.
Remember how we said the decibel was made for human ears? 0 is the baseline for human hearing, while the max we can handle before losing some stereocilia is—wait for it—100. If you listen to music or any sound above 100 dB for longer than 2 hours, you'll probably develop hearing loss.
Example Time
Lola was curious about how much each volume level increased the intensity (in decibels) of the flute death metal playing in her music player. She took some pressure measurements for the volume settings 1 – 5 out of the 10 total levels.
| Sound Experiment | Δp(Pa) |
| Volume 1 | .456 |
| Volume 2 | .507 |
| Volume 3 | .554 |
| Volume 4 | .603 |
| Volume 5 | .655 |
Δp(Pa) is just referring to the change in pressure from all those sound waves. To find the intensity (sound-wise; emotionally it's 100% intense), she used this formula in terms of waves over meters squared and dB (decibels).
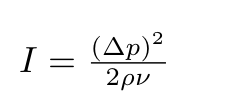
I stands for the intensity of sound using the change in pressure (Δp), the density of the material (like air or water) is ρ, and the speed of the observed sound (υ).
After that, Lola just converts the intensity in waves over air to the intensity in dB, β, which can be found by the equation:
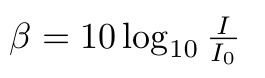
where I0 is the intensity of sound already hanging out in the environment.
(Source)
In her controlled lab environment, all that amounted to these calculations:
| Sound Experiment | Δp(Pa) |  |  |  |  |
| Volume 1 | .456 | 1.20 | 331 | 5.74 × 10-4 | 87.59 |
| Volume 2 | .507 | 1.20 | 331 | 6.38 × 10-4 | 88.04 |
| Volume 3 | .554 | 1.20 | 331 | 6.97 × 10-4 | 88.43 |
| Volume 4 | .603 | 1.20 | 331 | 7.59 × 10-4 | 88.8 |
| Volume 5 | .655 | 1.20 | 331 | 8.24 × 10-4 | 89.16 |
The dB never goes above—or even close to—100. Phew! That was a close one.
If Lola kept up the experiment, going to 10 instead of just 5, she probably wouldn't come anywhere close to 100 dB. What a load off.
Still, any sound over 85 dB used for long periods of time might not cause permanent damage right away, but it can still cause premature hearing loss. If you're going to Australia anytime soon, don't use your MP3 for the whole 16-hour airplane ride.
(Real talk: where'd you get your magical MP3 player that can run for 16 hours straight? Can you hook us up with one of those?)