Have you ever played on an indoor tennis court? It's just like being outdoors, except you're trapped in a very small space with a whizzing ball that could cause some serious damage to your insides. Aside from the physical damage, you might notice

• the sneakers screeching on the floor.
• the tennis ball smacking down on each side of the net.
• coach yelling at players and/or the ref.
• players whispering to each other.

All that happens in a normal tennis court, but it's so much louder in that small, concrete box. Put it all together and you've got an incomprehensible blob of sound.

Why does putting the game in a concrete box mess up the sounds so much? A little something called the superposition of waves. The superposition of sound waves means that the waves add to (or subtract from) each other to create a massive (or zero) amplitude sound wave.

All that adding can be traced back to your high school trig class. (If it's been a while since you've been near a high school trig teacher, check out Shmoop's trigonometry guide.) Sines and cosines are very interesting functions but adding up n sines and cosines together gets complicated if n is anything larger than three.

An indoor tennis court is a cube: it has six sides. Good luck with that.

If you took any basic trigonometric identity to that indoor tennis court, it would say, "Nope, I can't add that many oscillatory functions (it means the sound waves) simply. There's just too much going on for me to find a simple formula."

But…actually that's wrong. For starters, trigonometric identities can't talk. Heh, heh.

For another—more serious—thing, we only need to use what a Scottish mathematician named John Napier invented. With his help, we can add up all the waves, get an accurate amplitude (the height from the middle of the wave to its highest point), and still keep track of the phase information (how far away it is from the origin).

(Confused? Check out our learning guide on waves. It's going to tell you all about amplitude, phase, and even a bit on Napier.)

Nice work, Napier.

Yep, all Napier needed was a little help from his number one fan, mathematician Henry Briggs. When you're finding the amount of sound produced by waves in a closed space, all you have to do is introduce a placeholder function called a logarithm, or "log" for short.

Does that sound familiar?

Here's what it looks like in math terms:

 

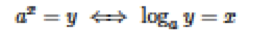
With logs, you can turn the product into the sum, which makes life oh so much easier in trigonometry and geometry. Usually, when combining waves, we'd need to multiply the values of the waves. Once we introduce logs, though, all of the sudden multiplication can become addition.

These log and exponent properties may be useful for this slightly more challenging problem involving the use of natural logs.

Yeah—not "fireplace" natural logs. Natural logs have a base of the number e (that constant we love using for calculating money). e happens to be completely irrational and shows up all the time in nature. Hey—maybe that's why they call it a natural log?

Mind…blown.