When's the last time you played in a pool? How about the last time you played the game pool? Or maybe you played pool in the pool by pooling your pool toys?

However you pool, you can get some great examples of waves moving through materials. Yep, especially the version of pool where you use sticks to poke balls into holes. When you get right down to it, all waves have energy. The moment you hit that cue ball with your pool stick, you're sending a pulse of energy through the ball in a wave motion.

In order for this mechanical wave to work, you'll need a material for the wave to move through. The material itself doesn't move…but its particles do. When the particles move, the energy of the mechanical wave is transported from one particle to another, causing a shift in the material.

 

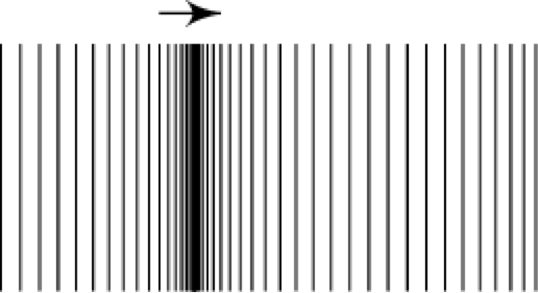
The molecules in the material get compressed (squeezed together) and contracted (pulled apart), as a result of the energy being sent through the material. These compressions and contractions happen because the moving energy causes a pressure build up, known as momentum.

If you watch the movement of

• seismic waves,
• jump rope waves,
• ocean waves,
• Slinky waves,
• guitar string waves,

you're watching mechanical waves in action.

We can break things down further, though. There are also three categories of mechanical waves:

• Transverse waves
• Longitudinal waves
• Surface waves

Mechanical waves share some of the same properties as electromagnetic waves (which is why they're both called waves, FYI), like amplitude, wavelength, and period.

 

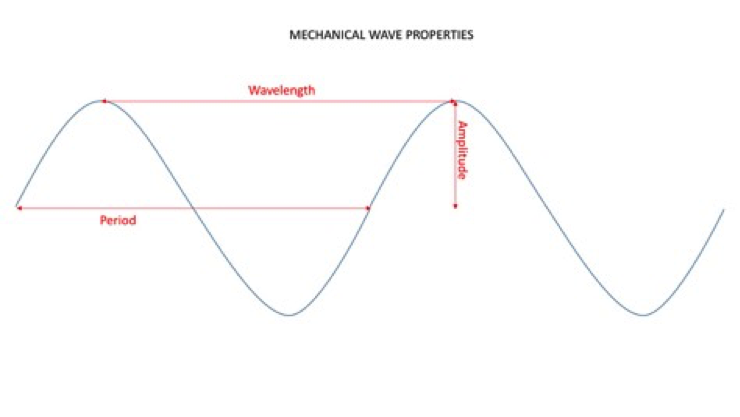
In a wave, you've got a couple of different properties:

1. Amplitude (A) is the height of the wave, starting at the midpoint of the wave. When a wave moves up and down, it has a central point that it crosses. Amplitude measures the distance between the peak and the midpoint.
2. Wavelength (λ) is the distance between two side-by-side wave peaks.
3. Period (T) is the time it takes for a full wave to reach the peak and trough (the bottom-most point). The period is the amount of time it takes a wave to complete one full wavelength.
4. Frequency (f) is the number of complete waves per second.
5. Wave speed (ν) is the speed of a wave as it moves through a material.

A wave will move a distance of one wavelength in one period, creating a frequency of the number of wavelengths it makes in a second. When you're working with these different wave properties, you can also bank on these facts:

 

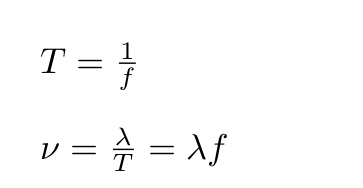
Example One

Let's say that a jump rope turns at

ν = 2 m/s

If the jump rope has a wavelength of 6 meters, we can figure out the frequency without hurting any jump ropers (hopefully).

Since ν equals 2 m/s and ν = λf, which is 32m × f, we can write this as:

 

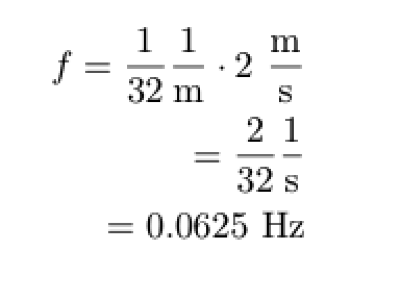
Example Two

Say you're being chased by a crocodile. Why?

…Why are you asking so many questions? You're being chased by a crocodile; you've got some bigger problems here.

Even though you've got some large, toothy problems to deal with, you start thinking about that big old crocodile tail. (Maybe your mind wanders too much; we aren't going to judge.) As you run, toppling a trash can to slow down that relentless, scaly crawl, you notice that the croc's tail has a frequency of 12 Hz and the oscillation is 3 meters per second, or:

 

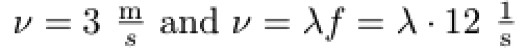
The equation to find the length of the tail can be found by solving for λ:

 

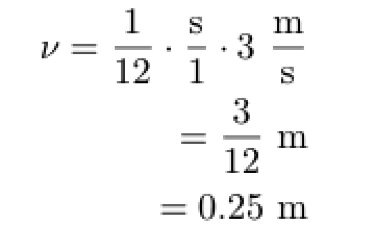
There you go; it's only a quarter of a meter. Now get running.