Now that we’ve totally sold you on these two hassle-free ways of graphing lines, let us teach you how each method works. We promise, these are not rip-offs like some infomercials. Why did we ever buy that potato peeler that doubles as a laser pointer?
The first method is the slope-intercept form. It looks like this:
y = mx + b
We know that m is the slope of the line, but what is b? We may not be a world-class detective, but we're thinking it's an intercept of some kind. It turns out that b is the y-intercept specifically: (0, b).
If we're given an equation in slope-intercept form, we immediately have the slope and one point on the line, making it a cinch to graph. Alternatively, if we know m and b, we can quickly create an equation for the line. This form is handy no matter which end we're starting from.
Sample Problem
Graph the equation y = 2x + 1.
This is in slope-intercept form, so we know that the number in front of x is the slope, and that 1 is the y-intercept. Our brains are just bulging with knowledge, and we haven't even started yet.
Plot the y-intercept to start, at (0, 1):

Next, because we know that the slope is 2, also known as  , we know that another point will be two units up and one to the right. That puts us at (1, 3). Remember, the 2 may come first in the slope, but the rise is in the y-value, which is second in our point.
, we know that another point will be two units up and one to the right. That puts us at (1, 3). Remember, the 2 may come first in the slope, but the rise is in the y-value, which is second in our point.

How about we do one more, just to be safe?
Sample Problem
Find the equation of the line for the following function.

Wait a second, "just to be safe"? That makes it sound like we would have been unsafe if we didn't do this problem. We didn't mean that as a threat, honest.
The y-intercept of this line is hanging out right in the middle of -4 and -5. So, b = -4.5. Now for the slope. Let's start at (-3, -3) and work our way over to (-1, -4). Both of them are on the line, and they have the distinction of not being fractions. Sorry, fractions, but you're hard to work with.

Our rise is -1 and our run is 2. This gives us a slope of  . The pieces have all been gathered. Let's assemble them, Voltron style, into a space robot-fighting equation for the line.
. The pieces have all been gathered. Let's assemble them, Voltron style, into a space robot-fighting equation for the line.

Yes, this looks like an equation capable of taking on Zarkon. Totally.
Example 1
Graph this line by using its slope and y-intercept. |
Example 2
Graph this line by using its slope and y-intercept. -3x + y = 2 |
Example 3
Write the equation of the line for this graph.
|
Exercise 1
Graph this line by using its slope and y-intercept.
y = 2.5x + 7
Exercise 2
Graph this line by using its slope and y-intercept.
Exercise 3
Graph this line by using its slope and y-intercept.
y = 3 – 2x
Exercise 4
Find the equation of the line in slope-intercept form for the following graph.
Exercise 5
Find the equation of the line in slope-intercept form for the following graph.

 . We can also tell that you've been working out lately. Good on you.
. We can also tell that you've been working out lately. Good on you.


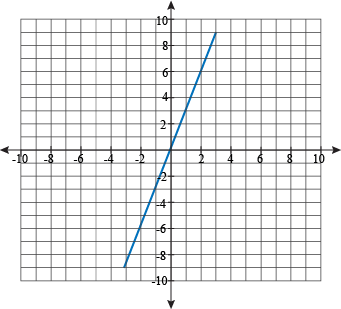




 and the y-intercept is -4.
and the y-intercept is -4.