Sometimes, a little bit of work needs to be done before we can start solving trig equations. (cos t)(0.9 + sin t) = 0 In this case, we need to factor out the common term, cos t. If either factor equals zero, the whole equation will. cos t = 0
0.9 + sin t = 0 Cosine equals zero for 0 and π radians on the unit circle, and all of their coterminal angles. t = 0 + 2πn
t = π + 2πn OR t = πn Now we can find angles for sine. sin t = -0.9 sin-1 (sin t) = sin-1 -0.9 t = -1.120 radians 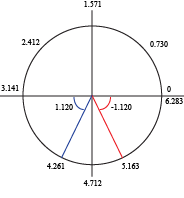
That's only one angle though. -1.12 radians is in the fourth quadrant. Sine of an angle in the fourth quadrant is negative, so our other angle must be in the third quadrant. π + 1.120 = 4.261 radians t = -1.120 + 2πn
t = 4.261 + 2πn These are the infinite number of angles that will make sine equal -0.9. However, we really wanted the angles that satisfied our original equation (waaaaay up top there). Including those from cosine, they are: t = πn
t = -1.120 + 2πn
t = 4.261 + 2πn Finding the right answer satisfies us almost as much as it does the equation. |