Computers don't really "get" negative numbers. As far as they're concerned, everything's either a zero or a one. That's great and all, but we live in the real world and need ways to trick the computer into storing negatives for us.

Signed Magnitude

If you just want to represent the number (without doing fancy math like adding and subtracting), include another 0 or 1 at the far left-hand side of the number as a "signed bit." The signed bit tells—you guessed it—the sign for the number: 0 for positive numbers and 1 for negative numbers. The catch? you can have a positive and negative version of zero.

Yeah, we don't get it either.

We left out a pretty important part of doing math on computers…actually doing any math. If you add -3 to 4, for example, you should get 1 as a result. Key word: should.

-3₁₀ is represented as 1011 including the signed bit and 4¹⁰ is represented as 0100. After adding them together, you should get 0001.

Adding in binary is just like adding in base 10, except every time you add two ones, you get a zero and carry a one to the next place. Let's make a mini-algorithm:

• 0 + 0 = 0.
• 0 + 1 = 1.
• 1 + 1 = 0, carry the 1.

There's no way to represent two in one number in binary, just like there's no way to represent eleven with one number in base ten. It's just like adding two numbers in decimal notation to get a sum greater than ten. If you add together 6 and 8, you'll end up with 4, but you need to carry the extra 1 to the next place in order to represent fourteen. That extra number is called the carry.

Adding 1011 and 0100 looks like this:

[Gulp]

Good thing we have other systems to represent negative numbers in binary. Computers (and people) need to do math. Preferably correct math.

Two's Complement

To make binary numbers add together without, you know, ending up with -3 + 4 = -7 (can you hear the mathematicians cringe?), use two’s complement.

Two’s Complement could also be called "Signed Bits 2.0." In the opposite of signed bits, the leftmost value is reserved so that

• negative numbers start with a 0. 
• positive numbers start with a 1.

This time, though, negative numbers are represented by flipping all of the bits—every single bit—in their positive counterparts. All the 0's will turn to 1's and all the 1's will turn to 0's. Then another 1 is added to the entire number.

Altogether, the process for manipulating -3 would be:

• Binary Three Plus the Signed Bit: 0011
• Bits Post-Flipping:: 1100
• Adding One: 1101

Now when you add -3 to 4, you get 10001.

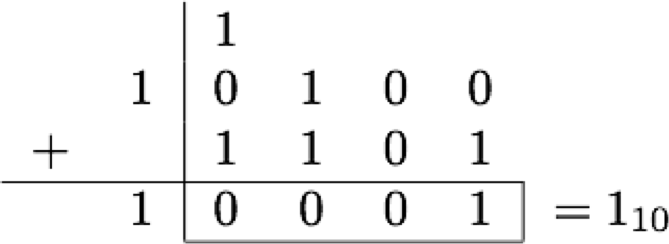
Mission accomplished.

The extra one might look like it's going to make the number positive, but that isn't true. Instead, that extra number's going to be considered overflow, so it's just going to fall away from the four bit representation (everything inside the box).

This method works because you're essentially counting out how many numbers away from zero a negative number is—which is kind-of the whole point of negative numbers. For more on that, check out this page from Cornell.

The range of numbers you can write using this system goes from -(2^{n – 1}) to (2^{n – 1} – 1) where n is the number of bits. In a four bit system (i.e. the one we used for the example) you can represent everything from -(2³) to (2³ - 1) or from -8₁₀ to 7₁₀. An eight bit number system can range from -64 to 63. And…you get the idea.

Eight bits is also known as a byte. John Tukey, a mathematician known for his work in statistics, coined the term "bit" as an abbreviation of "binary digit" in the late 1940s. (Source)

Just like Shmoop, computer scientists also love

• puns.
• food.

All that to say: there are eight bits in a byte and only four in a nibble.