Say you're at a fancy restaurant because your parents want to celebrate something irrelevant to you but apparently important to them. Fancy restaurants are great if you like weird little bits of food that probably aren't even cooked.

Uh…no thanks.

Just a burger, please. Cooked. When you get that burger, it's about four feet tall and there's no human mouth on earth that can take a bite that big. You have to break your burger problem down into more manageable bites, so you have to eat it with a knife and fork, which is probably the point. A fancy restaurant can't just give you finger food. Otherwise, they wouldn't be able to charge you for the gold-plated sporks.

When you're confronted with a burger that's too big to eat, you break it down into bite-sized chunks and eat those. You can do the same thing in dynamic programming, too.

…Minus the fancy silverware. (Goldware?)

If you want to apply dynamic programming to a problem, the solution needs to have something optimizable—you need a way to say, "Yup, this solution is the best one." It can't just be optimizable, though. It also needs to have an optimal substructure. You need to be able to find that optimal solution by finding the optimal solution of its sub-problems (source).

So much optimizability.

Sound confusing? It's simpler than it sounds. A sub-problem has an optimal solution if there is only one right answer. There can be only one.

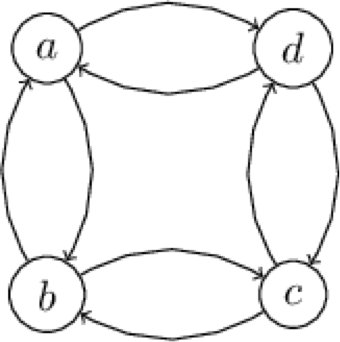
Take the diagram above. If the problem's about finding the shortest path from a to d, then the best path is a → d. It's either that or go from a to b to c before you finally get to d. Yeah…no. This problem definitely has an optimal substructure because there is obviously only one optimal (read: right) answer: a → d.

If you're looking for the shortest path from a to c, things get a little trickier. That problem does not have optimal substructure. Just look at the ways you can get to c:

• a → d → c
• a → b → c.

We don't know about you, but those two paths look equal to us. Even the middle letter is the same shape flipped.

Before you can start programming dynamically, you need to know whether the sub-problems have optimal solutions. It doesn't work just to look at the original problem. Dynamic programming is all about facing huge problems without clear solutions or even clear places to start. To get to a solution, you have to break down the problem until you get problems small enough to determine whether they even have optimal solutions.

All that work just for a hamburger.