It's vacation time, and this time you've decided to make your time count: you're going bog snorkeling. As much as you'd think the prize money is for this competition, you still have a bit of a budget getting to the World Bog Snorkeling competition in Wales.

There are thousands—literally thousands—of ways to get to Wales, but some are a little better than others. Snorkelling across the Atlantic might save money, but the cost of

• food
• swimming gear
• hypothermia

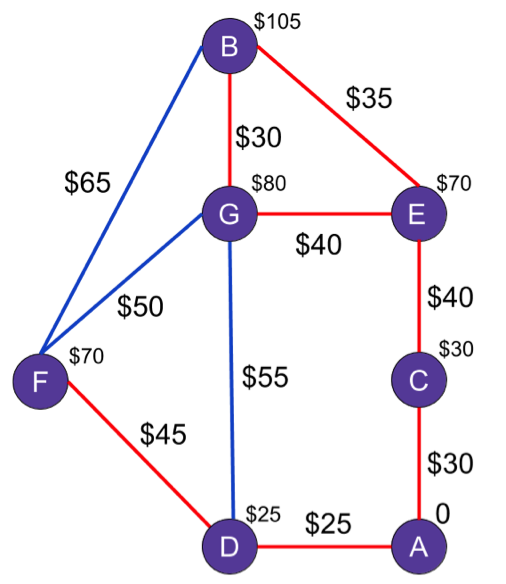
is higher than you'd think. Instead, you decide to make a map of the paths you could take by using trains and buses, weighting each edge with the amount of money it'll take to go between each node. Here's what you come up with:

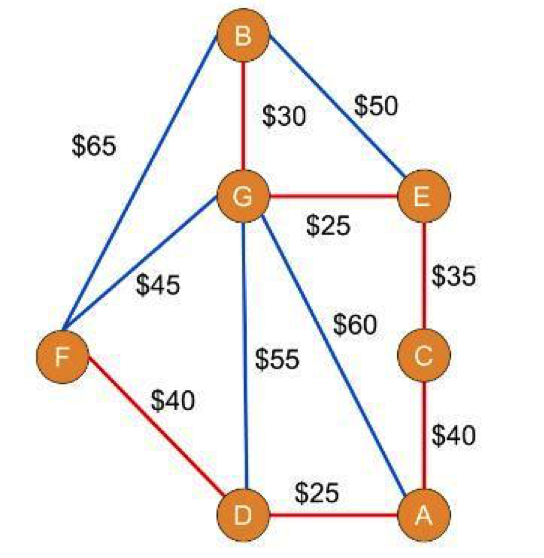
So what's the cheapest way to get there, ignoring the physical impossibility of taking a train or bus across the ocean?

Before you go trying to follow every possible route, maybe you'd like some help from Dijkstra’s Algorithm, which is guaranteed to find you the cheapest path between two nodes on a weighted graph.

Say you're starting at A and need to get to B. The first step is to set the costs of getting to any other node at infinity. That's going to help with dealing with unexplored nodes later. Infinity is basically a placeholder until we can give the algorithm more concrete costs. The only cost set in stone at this point is A, which is 0, since…that's our starting point. We'll set the cost of A to look like this:

C(A) = 0

Any time we establish a cost of getting from one node to another, we're going to call it C(node), which stands for "the cost of the node." In the example, we're literally dealing with the cost, but cost could count as anything from time spent getting there to the number of gummy bears you have to eat. It's a pretty flexible term.

In the graph, we'll put the cost at every node so that everyone knows the difference between the weighted edges (the cost of going between two nodes) and the cost—which is the overall cost of the path.

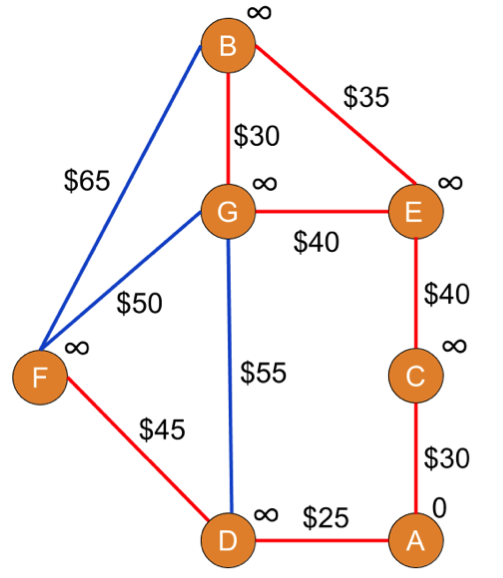
To check whether the path is actually going to take us infinite moneys to get somewhere, we'll need to do some number crunching of the Dijkstra variety.

1. Start at the node with the lowest cost. At the beginning, that's A, with a cost of—wait for it—0. 
2. Now pick a neighbor of that node (in the case of A: either D or C; let's go with D).
3. If the cost of the node ($0) plus the path to the new node ($25) is less than the current cost of new node (∞), you've found the new shortest path to the new node. Nice work.
4. If you did find a new shortest path, update C( new node) to equal that new shortest path. 
5. Move on the next neighboring nodes and do the same thing. 
6. Once you've searched all the neighbors, add the node (A) to a list of visited nodes. 
7. Go to all of that node's neighbors, checking their neighbors for shortest paths. Continue finding the shortest path until you've either the destination node's added to the list of visited nodes (in this case B) or you've visited every single node.

Let's do an actual walk-through now, shall we? We start at A because it's the cheapest and calculate a new C(C) and C(D) in that order, based on the weights of each edge. Since $30 and $25 are all less than the current costs of infinity for each node, we can update each node’s cost and add A to the visited list (marked in purple).

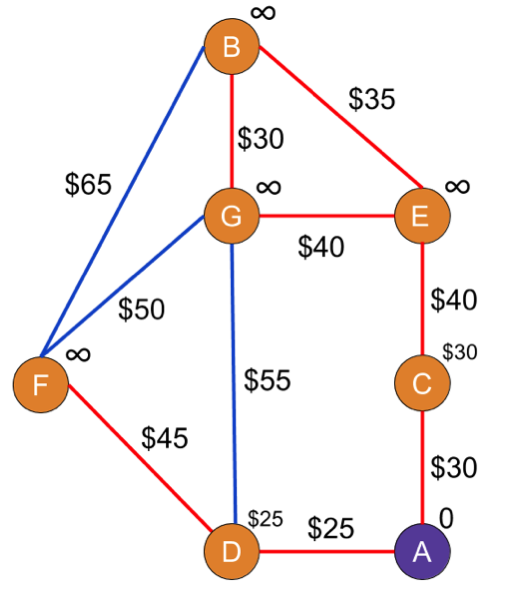
To pick the next unvisited node, we'll find the cheapest node, which is going to be D, at an impressive rate of $25 to cross the Atlantic.

Though you'd probably be crossing in a life raft.

Anyway, D’s unvisited neighbors are G and F. Since C(D) = $25, we'll find C(F) to be

C(F) = $45 + $25 = $70.

That's a little lower than the current C(F) (which is infinity), so we'll update the cost.

The new C(G) is:

C(G) = $25 + $55 = $80

In a shocking turn of events, that's also lower than infinity, so we'll update C(G) too. Now D can go on the "been there, done that" list.

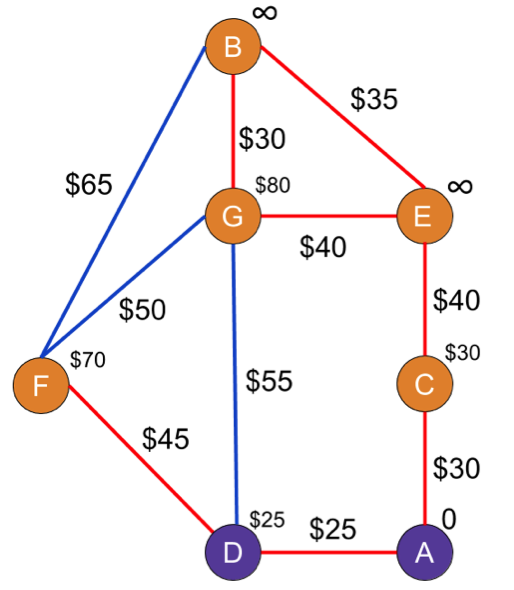
Now the cheapest unvisited node is C. C’s unvisited neighbors are…just E, so we'll calculate its new cost. Since the cost is definitely less than infinity—$70, btw—is updated. Now C can go on the "been there, done that" list and get a nice purple look.

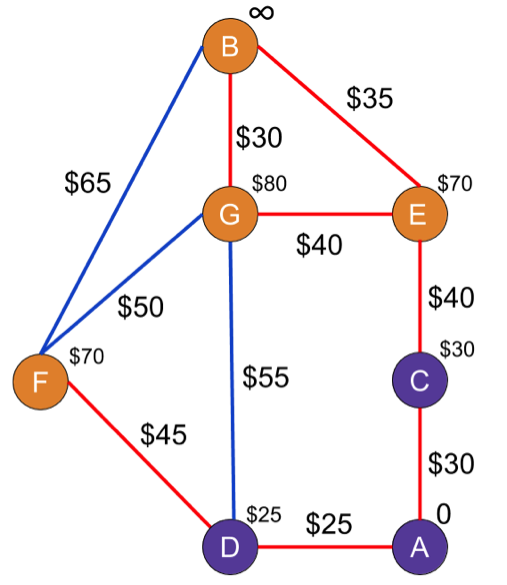
Next on the list of cheapest nodes, there's a tie between E and F. For the arbitrary reason that F was found first, we're going to check out the cost of its neighbors—B and G—first. G's already been checked once, but the path from A to D to F to G could be less expensive than A to D to G, so we'll have to check it. C(G) for the new path is $120 (that's C(F) + $50), which is less than $80, so we'll keep the original cost.

C(B) hasn't been visited yet, though, so it's guaranteed to get the new cost of $135 from the A → D → F path. Then we'll add F to the list of visited nodes.

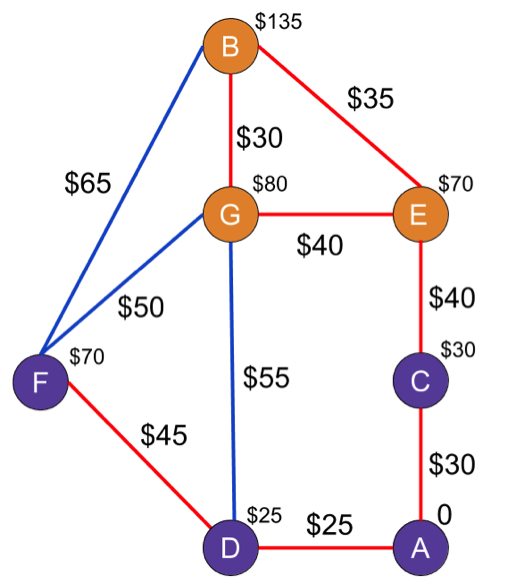
Done, right?

Not so much. We might have found one path to B, but we haven't found all the paths to B, and one of them could be cheaper. We can't call it a day until B has the cheapest path to be analyzed in the list.

The next lowest cost node is E, so we'll look at its unvisited neighbors, B and G. G’s cost isn’t updated because the new cost, $110, is more than the current cost, $80. B’s new cost would be $105, though, making it much less expensive than its current cost ($135). Now that C(B)'s set to $105, we're done with E.

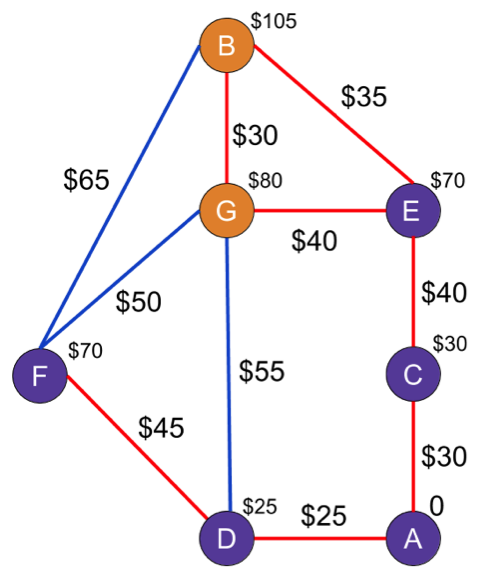
On to G. The only unvisited neighbor left is B, and the cost to get there from G would be $110. Not bad, but it doesn't beat B's current price of $105, so nothing changes. G gets added to the list of visited nodes and we head to the final node: B.

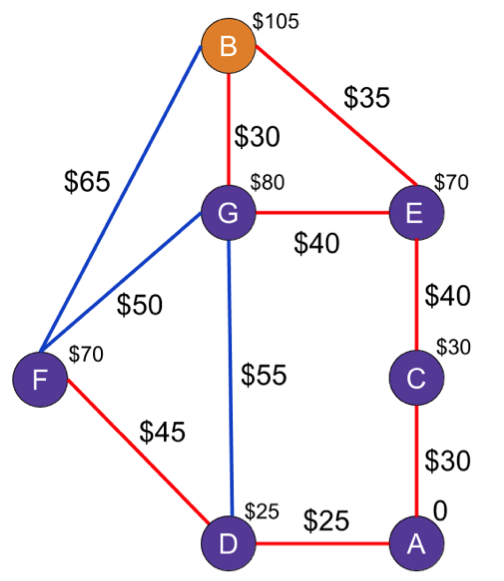
Since B has no unvisited neighbors, we can just add it straight to the list of visited nodes, meaning we're done running the algorithm and it's going to cost us $105 to go snorkeling with the cranberries. Bet you don't get to say that every day.

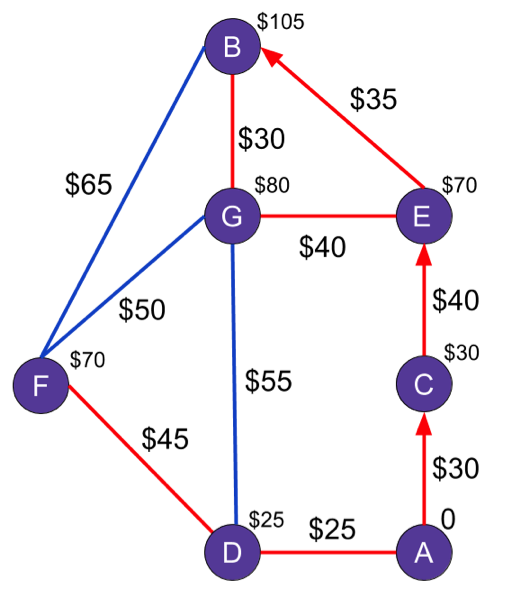
And the winning route is:

A → C → E → B

Now all that's left is remembering to pack your nose plugs.