Think back to the last time you needed to find something. Maybe it was your keys, phone, favorite sci fi movie with a terrible premise (and probably a terrible execution, too), or that CD you found at a flea market filled with kazoo covers of pop songs.

No matter what you're searching for, whether it's heartfelt kazoo covers or a Razzie-worthy film, it probably took some time before you finally found it. Especially if you spent all your time rooting around a messy room. But—stop us if you've heard this before—you can actually save time searching if you put everything in one place.

Less time searching, means more time watching terrible movies like Attack of the Killer Tomatoes.

(Just don't visit a vegetable aisle right after watching.)

In the same way that you can choose to keep your movie collection on a shelf instead of scattered under dirty clothes and sports participation trophies, keeping data in lists can make searching for things that much faster. In fact, it takes a maximum of the length of the array to search for any one element.

There's just one little problem: if you're using a stack or a queue, you could potentially lose elements when you're searching for something. Every time you pop or dequeue an element, you're physically taking it out of the list. When searching, that's usually less-than-optimal.

Searching Stacks

In a stack, because you can't see anything except the top element, you have to pop off one element at a time to search for something. If you aren't careful, all those popped elements can get lost in the computer memory.

How to avoid this Finding Dory-esque scenario? Just make another stack.

Any time you pop an element off of your first stack, you push it onto the second. Then, once you've found the element you wanted, you can just pop all the elements from that second stack back onto the first. You won't lose anything; you'll even maintain the original order of the stack.

Wait, what?

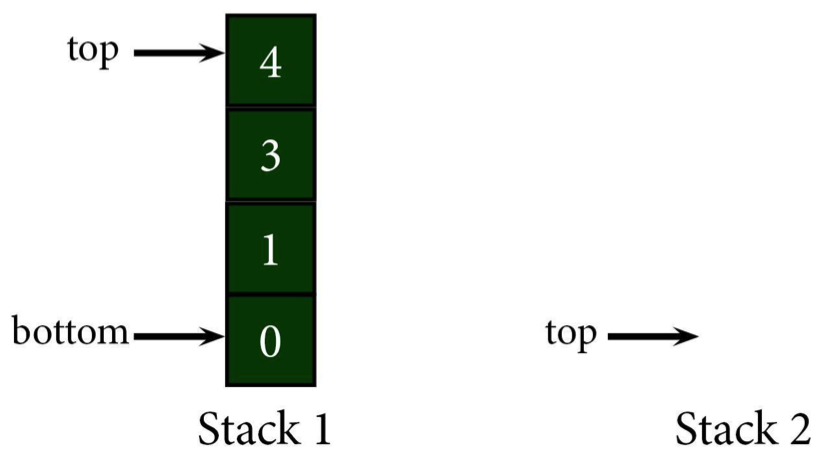
Let's say we have a stack filled with numbers and wanted to find 2.

 

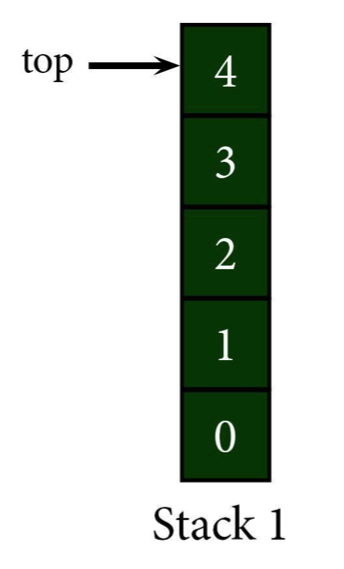
First, check the top (using the peek function, usually). When you find that 4 doesn't, in fact, equal 2, pop it off the stack. Before it's lost into the netherworld of the RAM, push it onto a new stack (we'll call it Stack 2 for clarity and also lack of originality).

 

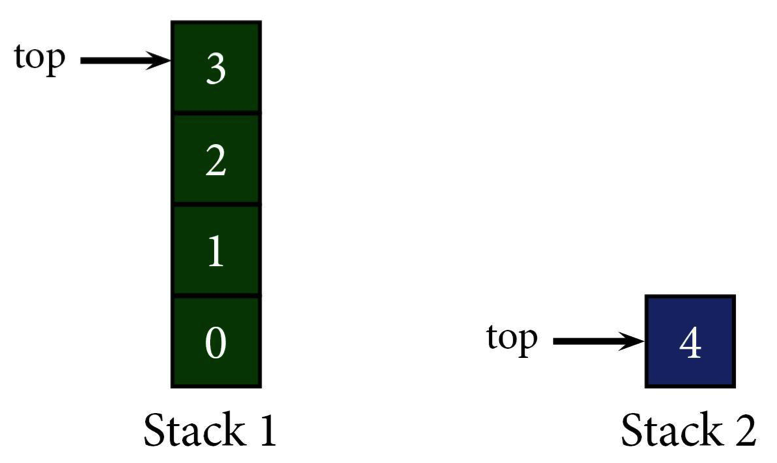
Peek at the new top of the stack (3), and find that it also doesn't equal 2. That means it gets added to Stack 2 as the new top.

 

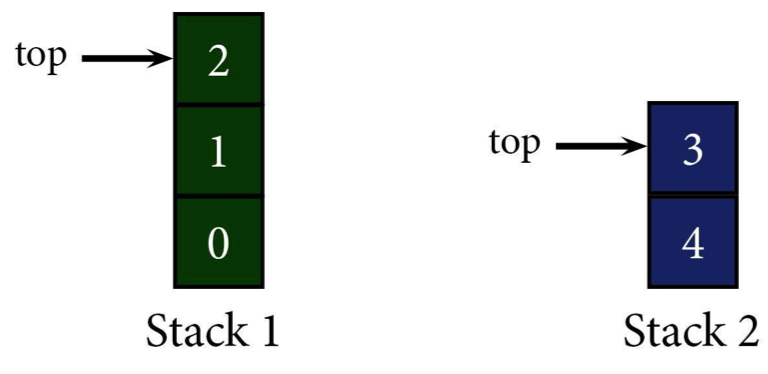
After peeking at the new top of Stack 1, we've found the element we need. That means we can stop popping things off the stack.

If we wanted to remove 2 altogether (maybe a 2 insulted Mama Shmoop or something), we could pop it from the Stack 1 without pushing it to Stack 2.

 

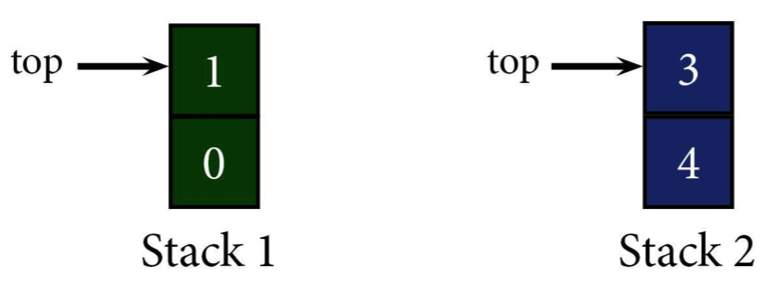
Now that 2's taken care of, we can put the remaining stack together. All we need to do is pop each element off the top of Stack 2 and push it back on to Stack 1. That means Stack 2's now empty and Stack 1's in order (minus 2, of course).

 

Everything's been searched and put back in order, but searching in stacks usually takes a lot of time and resources. In fact, if you have to search through the whole stack, you might end up having to basically pop/push the entire thing to another stack and then pop/push it back to the original.

That's usually more trouble than it's worth, if you ask us.

Searching Queues

Just like with a stack, when you take an element out of a queue (when you dequeue it), you need to be careful of not deleting it unless you absolutely need to do so. If you don't want to throw elements away, you'll need to use a second queue.

First, peek at the front of the queue to see if it's the element you want. If it isn't, dequeue it from the first queue and enqueue onto the second queue. Rinse and repeat until either the first queue is empty or you find the element you want.

Once you've found that element, you can do the opposite same thing you did with the stacks: dequeue the rest of the first queue and enqueue it onto second. The second queue can now become the actual queue and no one will know the difference.

Let's look at an example to help show how that all works.

 

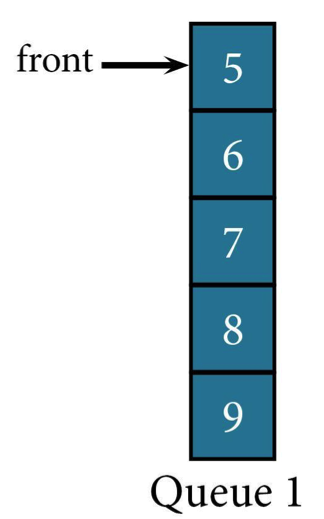
If you wanted to find number 7 in this queue, you'd first need to dequeue 5, then 6 (in that order) from Queue 1 and enqueue them onto Queue 2.

 

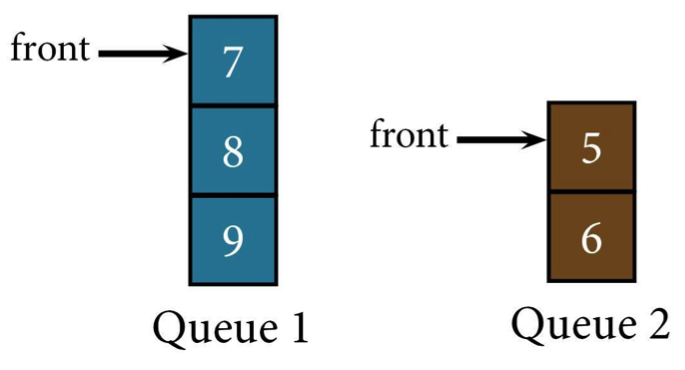
If you want to delete 7 (it probably deserved it), just dequeue it without adding it into Queue 2.

 

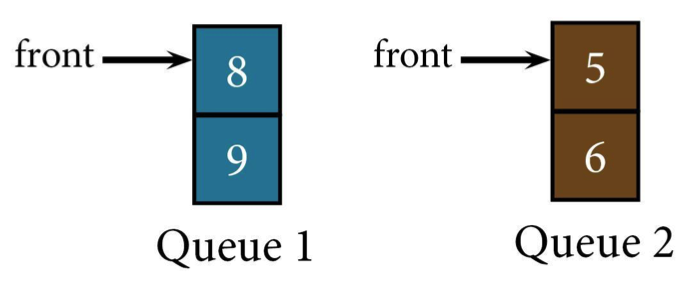
To put your queue back together, dequeue 8 and 9 (in that order) and enqueue them onto Queue 2. Now the queue's back together, it's just at Queue 2 instead of Queue 1.

 

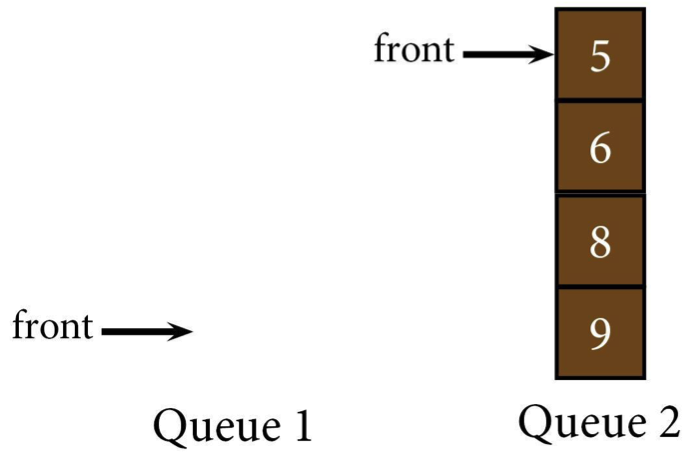
Just like with stacks, to search for anything, you have to dequeue and enqueue every single element. That's a lot of time and memory used.

If you need to search for things pretty often in your list, you might want to avoid the stack or queue all together and just go with a plain list. That way you don't need to constantly shuffle elements when you could just walk through the list itself.

We're just throwing that out there.