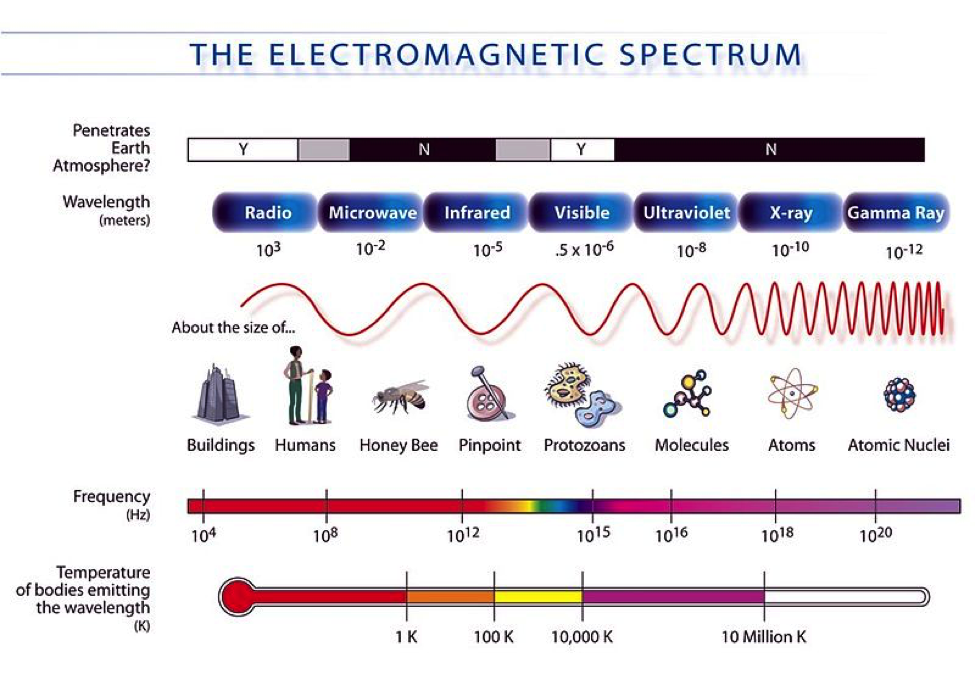
All the types of electromagnetic radiation are waves, and they're connected by their frequency and wavelength.

(Need a refresher on how waves look and act? Check out our learning guide on it. We even bookmarked the place that talks about wave properties. You're welcome.)

No matter the frequency or wavelength, an electromagnetic wave always travels at the same speed. To get to the same speed, something's got to give between the wave's frequency (how quickly it moves) and wavelength (how long it takes the wave to complete a cycle). The higher the frequency, the shorter the wavelength; the longer the wavelength, the lower the frequency. In fact, the relationship looks like this:

Speed of Light = Frequency × Wavelength

If you have a really tiny wavelength—we're thinking the size of your DNA—then you're talking about gamma rays, which have a really high frequency. If the wavelength is instead, say, the size of the golden gate bridge, then we're talking about long waves, which have a pretty low frequency in electromagnetic terms. Everything in-between is a different wave in the electromagnetic spectrum.

Electromagnetic radiation moves through the air using waves, making trigonometry kind-of important. Electromagnetic radiation might be invisible, but it moves just like ocean waves.

Think about what happens when you throw a pebble into water. The water ripples from that central point where the pebble hit the water. Those ripples move in what's called concentric circles—circles nested inside one another with a shared center. When those circles move through the water, they're propagating, which is a fundamental property of waves. The further away a propagated circle is from the center, the more strength the wave loses, making it look more like a line.

Electromagnetic Spheres

Electromagnetic radiation works just like that when it moves. It starts out from a source location—like an antenna—and propagates as concentric…spheres. By the time those waves have traveled a long distance, they lose enough energy to start looking like flat waves.

Here's where things get a little wonky. If you love fruit, grab an orange before moving on. It'll give you a model for what we're talking about and you can use it to fuel your brain. There's no downside here.

Unless you're allergic to oranges. Sorry.

Back to trig.

Let's talk about spheres in terms of oranges. If you cut an orange in half, you'll be staring at a circle. Luckily, an orange also has a natural radius when you cut it in half.

Just so we're all on the same page, the radius of a circle is the length between any part of the circle's circumference and its center.

A circle's usually defined by the length of its radius. It's a powerful piece of the orange. And by "orange," we mean circle.

Now let's take it all back to waves. If you take the square of a sine wave and add it to the square of a cosine wave, you'll get the radius of a circle squared.

Mind. Blown.

When you think about a sine wave, it oscillates—it moves away from and back to a line. While it's oscillating, that sine wave can reach a maximum distance from the center line; that's the wave's amplitude. That amplitude can also be the radius of a circle.

If you know your unit circle, you'll know that the radius of a circle can also be thought of as the right triangle it can make inside the circle. Take a circular orange slice and compare it to a sine wave, and you might notice something interesting about the height of the radius: each point can be mapped to a point on the sine wave. That trick also works with circles and cosine waves.

 

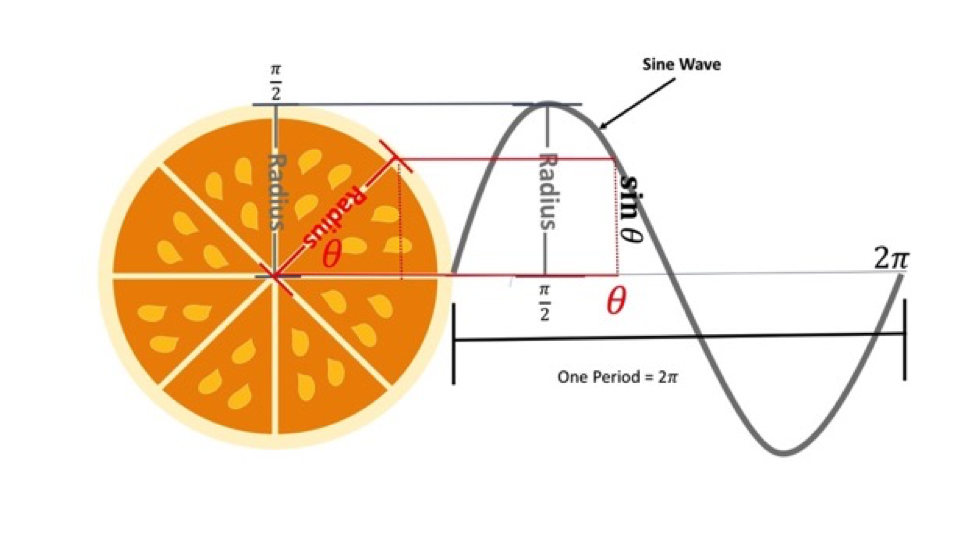
Yup; circles, waves, radii, amplitude, sines, and cosines are all related to each other—and radar technology has to use all of those relations to understand how electromagnetic waves move through space and objects. The amplitude of the electromagnetic radiation describes how much intensity the radiation has.

The phase is both related to the wavelength of the radiation and also determines how far the energy will travel through space—or a material like water, air, or plasma. When your cell phone makes a call, it's using wavelengths that are about a meter in size. When the wave makes one full period (i.e. it travels a meter) it's made it through one full rotation of a circle that's about a meter long.

Without trigonometry, we'd have a much harder time figuring out how cell phone waves travel and how we could get a signal from one phone to another.

What a scary thought.