Have you ever made sounds by rubbing the rim of a glass of water? Moving your finger around the rim physically creates vibrations that you'll hear as sound.

Sometimes it sounds great, and sometimes it sounds…less than great. (Sometimes when we play late at night, we're mistaken for a banshee. That's fun, don't get us wrong, but it isn't quite what we're hoping for when practicing "Flower Duet.") How can people tell the difference between great and less than great?

If it's been a while since you polished off your compass, you might want to glance at the Trigonometry module because we'll be using the concepts to talk about waves. We would regal you with some metaphysical rant about how field relates to every other field, but we've got things to do and radars to work.

In sound, the phase is going to tell us how much the wave has shifted and the amplitude is going to explain how loud it is. But back to the phase. That quality is going to tell us how uniform the sound is, which changes the quality of the sound.

A sound's pitch is a mix of the wave's frequency: specifically, how different wave frequencies can be organized in your head. Xylophones are great at organizing the sound waves according to frequency. Still, because of the way sound waves move, they need something to travel through, like glass, air, or xylophone wood.

(Whether that makes engineers good musicians is another story.)

Just like sound waves are vibrations that travel through the air (or any other material), electromagnetic waves are made from vibrations too. In this case, electromagnetic waves are vibrations that come from electrical and magnetic currents (at least as far as radar's concerned). As far as waviness goes, they still have frequency, amplitude and phase (how much it's shifted in terms of other waves). Any wave can be written as a cosine function as long as you have those values.

All waves fit into the wave equation.

For the wave equation to really work, though, we're going to need one more variable: the refractive index. That may sound like a tool Batman would use to fight crime, but it's actually just a way of explaining how the wave's going to change when it hits a particular material (every material has it's own index, by the way). When the wave hits a material like

• air,
• water,
• gummy worms,

it's being perturbed, because…it's been offset by the material. Scandalous.

The variable c represents the speed of light in a vacuum but if we want the wave to propagate through gummy worms, then all the gummy stuff inside those worms is going to slow down the speed of the wave. The refractive index of air is about 1 (same as the vacuum), but once you get into earth, wind, fire, and gummy worms, you'll need to either look up the index or run some experiments.

 

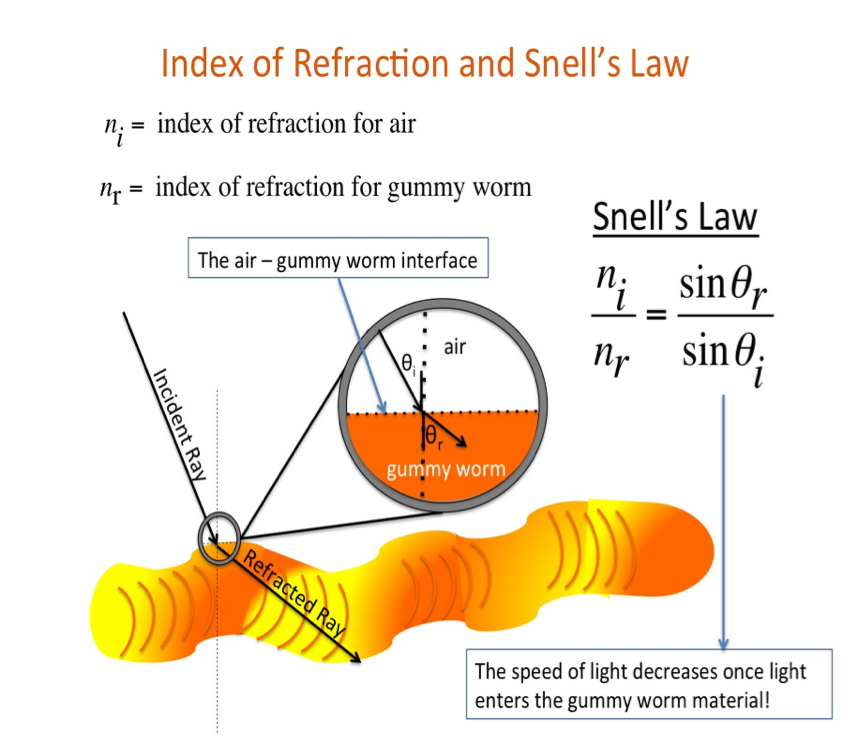
BRB, we're going to go get ourselves some gummy worms.