As much as computer scientists love hoarding their knowledge and techniques from the general masses, some concepts actually fit into other science-y categories too.

(JK about the "hoarding knowledge" bit, though. Computer scietists usually love sharing info…it's the people they talk to whose eyes glaze over whenever we get onto the subject of for loops and memory optimization.)

Recursion's one of those topics that technically belongs more to math than it does to computer science. Computer science just really loves it.

Say you're looking at a factorial number. To find a factorial n!, you need to multiply together every number from 1 to n. That means, if we're taking 5!, we'll need to multiply 5 × 4 × 3 × 2 × 1. To define it recursively, you could instead say:

5! = 5 × 4!

That definition doesn't really say anything, though. It just gives us another, slightly smaller, factorial to deal with. But the fact that it's slightly smaller makes all the difference. If we keep using the same recursive rule to break down the factorial, we'll get this:

5 × (4 × 3!)

We'll break it down a couple more times to look like this:

5 × (4 × (3 × (2 × (1))))

More generally, that recursive rule can be written as:

n = n × (n – 1)!

That's recursion: breaking a big problem into a smaller copy of the same problem to reach a solution. Except, instead of using code, we're using…math. This kind of problem is fantastic for solving sequences.

No really. We even have a learning guide on it. Here's the quick and dirty on it, though.

Sequences

Recursions go all the way down to mathematics, a place where recursive sets and sequences—like factorials—show up all over the place. Some sequences can even have multiple seed values (we're looking at you, Fibonacci).

When working with sequences of numbers, you might occasionally be able to find some general, non-recursive function that finds the n^th value without making you find every other value in said sequence. If you do, you've found a closed form, which and can be very simple or incredibly complicated.

One of the simplest is finding the sum of all the numbers from 1 to n, which has a recursive function definition that looks like this:

sum(n) = sum(n – 1) + n

If you don't feel like going all the way from 243 down to 1 with that equation, though, you can always just plug it into this, closed-form equation:

(n × (n + 1)) ÷ 2

Sets

Along with sequences, you can also get recursively-defined sets. This kind of set is usually a bit of a shortcut for sets that would be too tedious to list out. What's that? You think mathematicians are just being lazy. Okay, try listing out the set of all integers.

Go on, we'll wait.

It isn't so easy—even if you have an infinite amount of time.

To build a recursive set, mathematicians need to find a base case and one or more inductive steps (which, if we're splitting hairs, are really more recursive than inductive).

The set of all integers, Z, could be defined recursively as:

Base Case: 0 ∈ Z
Inductive Step: If x ∈ Z, then x +1 and x - 1 ∈ Z as well.

With the base case and the steps in place, it's pretty easy to inductively build up Z starting at 0.

0 ∈ Z, which makes 1 and -1 ∈ Z. 1 ∈ Z tells us that 2 and 0 are also ∈ Z (even though we were already aware about the zero one). -1 ∈ Z implies that 0 and -2 ∈ Z. We could keep going, but…we'll spare you.

In set notation, Z looks like this:

Z = {...-2, -1, 0, 1, 2, ...}

Fractals

Fractals are everywhere, whether you're talking about

• earrings,
• psychedelic album covers, or
• the paragon of uniqueness, broccoli,

math sure is beautiful.

One of the most famous recursive sets in math, the Cantor set, is actually a 140-year-old fractal. First, start with a plain, ordinary line.

 

Simple enough. Then copy this line again, but remove the middle third from it, giving you two pieces of that original line.

 

Rinse and repeat with the smaller lines.

 

By copying and erasing lines, you'll end up with what looks a little like a comb—a Cantor comb—or a very cool key.

 

You might want to sit down, because we've got some life-changing news for you.

By taking a simple mathematical (or, back to CS for a minute, programmatical) procedure, you can generate fractals without the help of a long-dead mathematician. Fractals are special because you can zoom either into or out of the pattern and it'll look about the same. The Sierpinski triangle, another infamous fractal, is created by dividing up a triangle into four pieces by throwing a triangle into the middle.

 

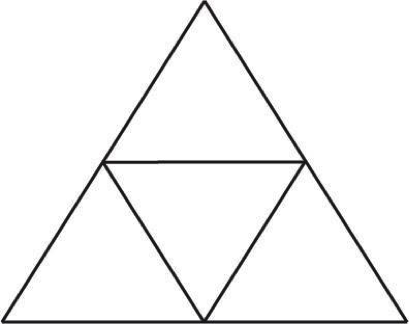
In each of the right-side-up triangles, you can throw another, smaller triangle into the middle just like with the biggest triangle. It'll look like this:

 

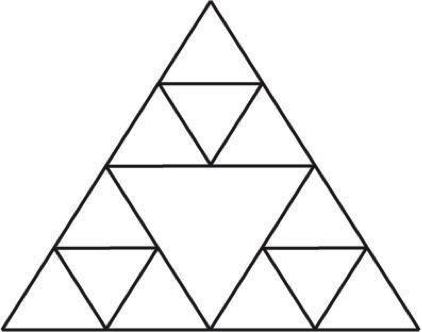
But you can keep going on the right-side-up triangles formed from these inverted triangles.

 

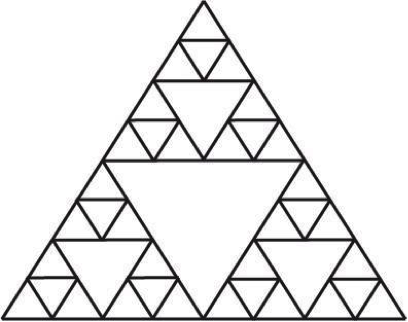
Pretty soon you've made a simple Sierpinski triangle, with each of the smaller triangle pieces looking like the whole thing in miniature.

 

If you want to get really fancy, you can even give the triangles a quick makeover and really to exaggerate the fractal…ness.

 

As long as you have some program that lets you draw shapes with your code, you can easily become a fractal master. Say you wanted to create a square fractal in code.

FUNCTION squareFractal(width, height, position)
	IF postition < 0.015:	#arbitrary size restriction 
						#that gives the base case
		RETURN
	
	ELSE:
		CALL drawSquare(width, height, position)
		SET position to 0.5 * position
		CALL squareFractal(width + position, height + 
					    position, position)
	END IF
END FUNCTION

If you write this in actual code (with a function that can draw a square to the screen, obvi), you'll get a fractal shape like this, starting with a 1 × 1 square and stopping after the square's height is less than a 64^th of an inch.

 

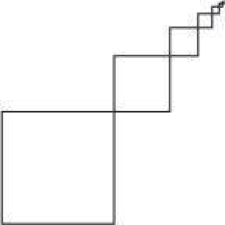
Both x and y decide where the top right corner of that square's going to be, and z decides the square's height.

Just remember, when coding recursively, always, always, always figure out your base case so that your program will eventually stop drawing that fractal. Maybe that's an arbitrary number. Maybe it's when the fractal gets so small that the computer can't draw them too easily. Like…say…when the square's less than a couple of pixels in diameter?

We’re just throwing that out there.