Is anything (or anyone) truly limitless? Sure, if we used all 100% of our brains, we might be able to write code one-handed (apparently), but even then you don't get superhuman-strength or anything. Then you'd be able to kill the bad guys within the first five minutes of the movie, and then what is there to do for the next hour and a half? Knit? Bake cookies? Make sure minor criminals show up to their court dates?

Nope, nothing has limitless power; it just wouldn't be fun to watch.. Recursion's the same way—probably not because it'd be boring, though.

Speed

As a rule, recursion's almost always slower to run than iteration. Yes really.

With recursion, you have to make so many function calls—and the computer had to sift through all of them before it can finish the recursion. Each function call takes some amount of time and the deeper your recursive function needs to go, the more that time tends to multiply. Even when the program finally reaches the base case, it'll need to back out of all those recursive levels, one by one, until finally reaching the original one.

Look no further than the Fibonacci sequence (and how you solve it using recursion) for an example of that one. For about 0 – 50, recursion's just fine. Once you start heading into the 60s and above, you'll notice some pretty significant lag time.

Let's examine the code for a sec to see why.

FUNCTION Fibonacci(FibonacciNumber) {
	IF n > 1
		RETURN Fibonacci(FibonacciNumber – 1) + Fibonacci(FibonacciNumber – 2)
	ELSE
		RETURN 1
	END IF
END FUNCTION

To compute the 5^th Fibonacci number, we need to compute both the 4^th number and the 3^rd. To get the 4^th number, we need the 3^rd and 2^nd numbers. To get the 3^rd number, we need the 2^nd and 1^st numbers…

See where this is headed?,

You could look at it like this:

 

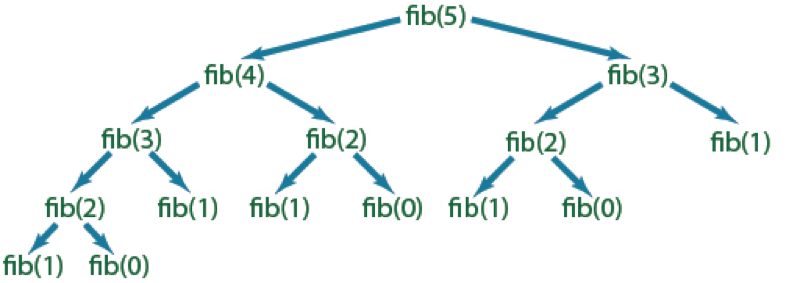
There's so. Much. Recalculating of the same numbers. In just the 5^th Fibonacci number, we're calculating the 1^st value five separate times. If we have to calculate the 10^th value, it's going to start getting ridiculous for charts. By 50 or so, it gets ridiculous even at their breakneck speed.

Some functions can be written more naturally using recursion, like factorials, where the definition of the algorithm is recursive from the get-go. At some point the time-to-ease-of-writing ratio just becomes too much to bear. Recursion may be quicker to write sometimes, but it's slow to execute. Iteration might take longer to write, but at least it's quicker to execute.

Choosing between the two depends on your priorities.

The Call Stack

Looking to cause a stack overflow on your computer? Recursive functions are the perfect tool for that job. Since a recursive function keeps calling itself until the base case is reached, more and more functions keep getting added to the stack before the base case lets them get popped off.

Call stacks have a max size to keep your programs in check; if they get too big and unwieldy, instead of letting the code overflow your entire memory and make your computer shut down, your computer's going to force it to crash with a stack overflow error.

You can avoid it with one handy trick.

Make sure your recursive function includes a reachable base case. There's no point in having a base case if nothing can ever reach it. Otherwise, you might not like the look of your program.

Or your computer.

If your function already includes a base case, you have two other options: use iteration or make it so your base case is easier to reach. Either one will lighten the load on that poor, overworked call stack, but tread lightly around lowering the base case's standards. Changing the base case could throw off the program's flow and give incorrect answers.

Real talk: choosing recursion or iteration all depends on the situation. If there aren't time/space constraints on program execution, write what's easiest for you to understand and work with.

(Source 1, Source 2)