Why are all of our comparison-based algorithms giving O(nlogn)? Why not O(n)? Or—even better—O(1)?

To know that a list is absolutely, positively sorted in a comparison-based algorithm, every element needs to be compared with every other element at least once. That means we can't have an O(1) algorithm.

Yeah, we're upset about it too.

But let's ignore the specifics of each algorithm and think about sorting in general. Say a cereal company came out with three brand new flavors: Sugar Coma, Sweet Tooth Decay, and I Can't Believe it's Not Chocolate.

There's nothing Shmoop loves more than synthetic chocolate product with 200% of our daily recommended serving of sugar. You want to try them all, but you aren't sure which one to buy first. It's a serious issue. If you represent the cereals with letters:

s = Sugar Coma
w = Sweet Tooth Decay
c = I Can't Believe it's Not Chocolate

Then you could buy them in six different orders.

At the very least, you can compare every element to every other element exactly once. If you compare n (three) elements n (three) times, the runtime's O(n²).

Ooooor, you could use a handy-dandy decision tree, which shows every way we could order the three cereals.

 

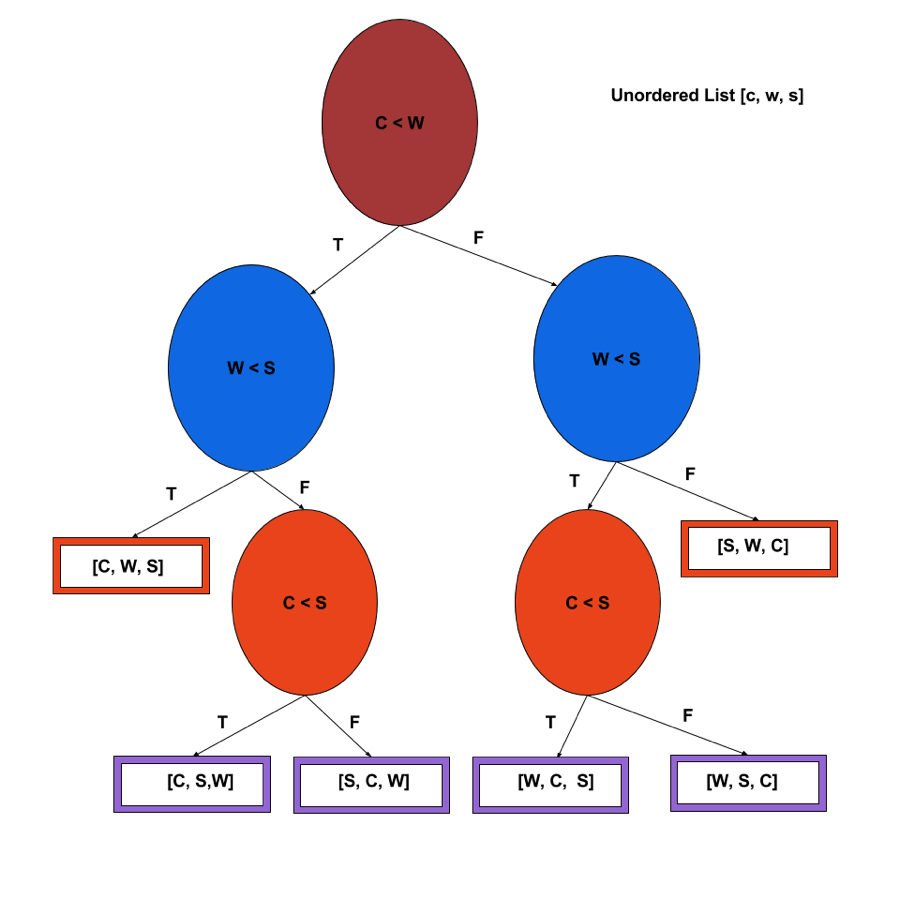
In the tastefully colored decision tree that shows every comparison with nodes—the circles—and every possible flavor ordering on a leaf—the rectangles. Because of all the possible combinations, this tree needs a certain number of levels—or a minimum depth—to actually list every way we could assault our teeth.

Mmm, synthetic chocolate product.

With every level of the tree that we add, we double the possible number of nodes, meaning that every time we add a layer, we multiply the number of nodes. Whenever there's a multiplication-turned-addition relationship, we know we've stumbled on something logarithmic.

There are 3! orderings, so…we need a minimum number of levels to have that many leaves. We could write out a proof with all the sums and the products, or we could not.

Trust us when we say that taking the log of 3! is greater than or equal to 3log3. If we were to look at a list of arbitrary length n, the height of the tree (and number of comparisons we'd need to make before finding the correct pairing) is

nlogn

which is the same runtime for Merge Sort and (sometimes) Quick Sort.

So when you're designing the next great sorting algorithm, shoot to make it run in nlogn time. Then treat yourself to some synthetic chocolate product.

Non-Comparison Sorts

Even if we don't need to represent the sort with a comparison tree, we still need to go through the list at least once, so the best we can possibly do is O(n) time.

But non-comparison sorts still rely on other things. Like Radix Sort, which needs to have a small number of digits or characters, these sorts could take more time or space (or both) than comparison sorts.

Tread lightly, young grasshopper.