Oh no, the stuffed animals are fighting again. They seem to think that they're ordered by how much you like them. (They are, but don't tell them that.) You need to re-order them before one of them starts losing stuffing.

Stuffed animals are tough to sort, but don't worry: we've got you covered. Let's look at a sorting algorithm where you sort items as you insert things into a list. We're going to cleverly name this sort "Insertion Sort."

This sort's super common for people working with small sets of data, so it's perfect for your collection of five stuffed animals. It all begins with a set of objects and an empty list where we insert elements as where they belong as we go.

 

(The first row tells us the index—where it lives in the list—of each stuffed animal.)

You'd create an empty space in front of you like so:

 

You then take the first element and put it in the first place in the empty list.

 

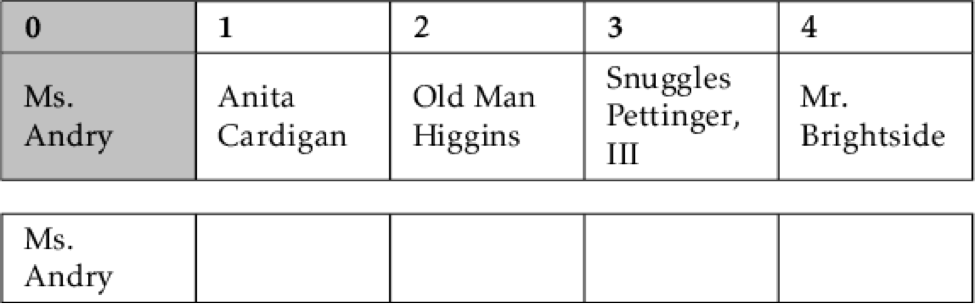
It's in a list of one, so of course it's sorted. Now you move on to the next stuffed animal and compare it with the first. Since the name Anita Cardigan comes alphabetically before Ms. Andry, move Ms. Andry to the right.

 

We've reached Old Man Higgins. We compare him to the last item, Ms. Andry, and find he comes alphabetically after her, so we put him at the end of the list.

 

Snuggles Pettinger, III, when compared to Old Man Higgins, comes alphabetically after Higgins, so he's placed in the next empty space.

 

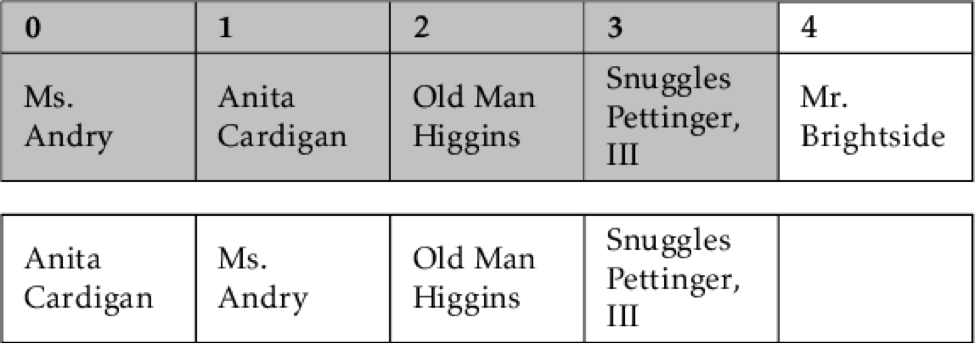
Now we've reached the end of the list with Mr. Brightside. Alphabetically, he comes before Snuggles, so we compare him to Old Man Higgens.

Again, Mr. Brightside comes before, so we compare him with Ms. Andry to find that he also comes before her. After comparing him to Anita Cardigan, though, we find that Mr. Brightside has finally found his rightful place between Anita and Ms. Andry.

 

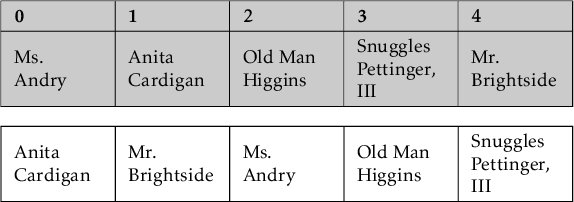
Alternative Implementation

You might want to sit down before we tell you a secret. We can actually do this same sort without the extra list.

Mind. Blown.

If we start by calling the List index zero a sorted list—since it only has one element—we can then go to the next index, pull the element out of the list, like so:

 

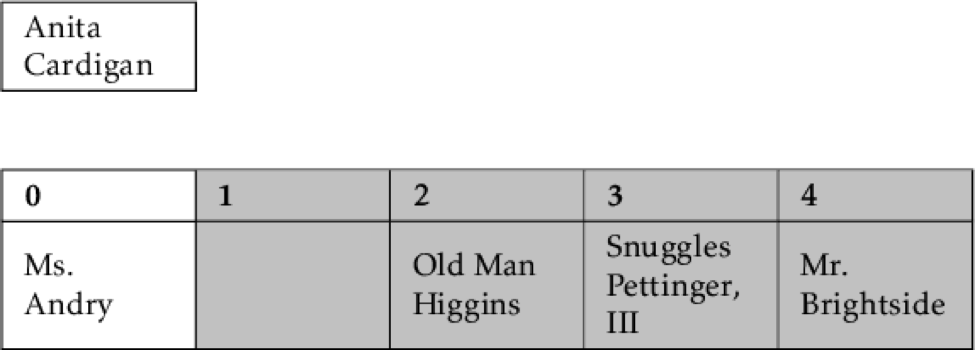
Once we find that Anita comes before Ms. Andry, we can shift Ms. Andry to where Anita was,

 

place Anita in the now empty space at index zero,

 

and call this section of the list as sorted. With Old Man Higgins, one comparison with Ms. Andry and he's already sorted, so we don't even need to pull him out. Thank goodness. Higgins has bad knees; we were a little worried they might give out if we moved him too much.

 

Snuggles doesn't need to move either.

 

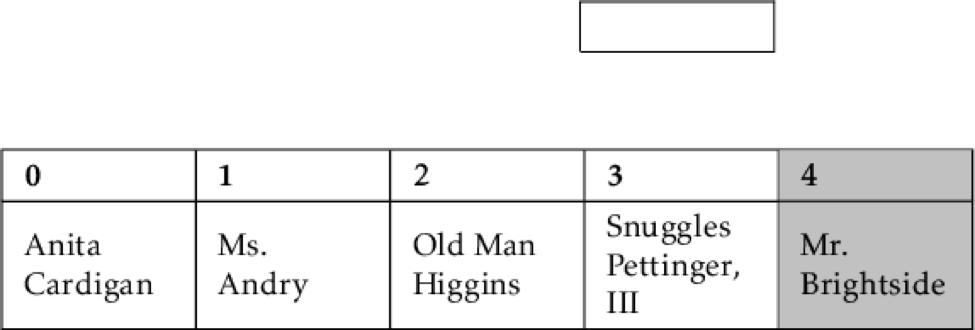
Now the fun starts with Mr. Brightside, the eternal optimist. Since we've compared him with Snuggles and found that Mr. Brightside should come first, we take him out and find that he also comes before Old Man Higgins.

 

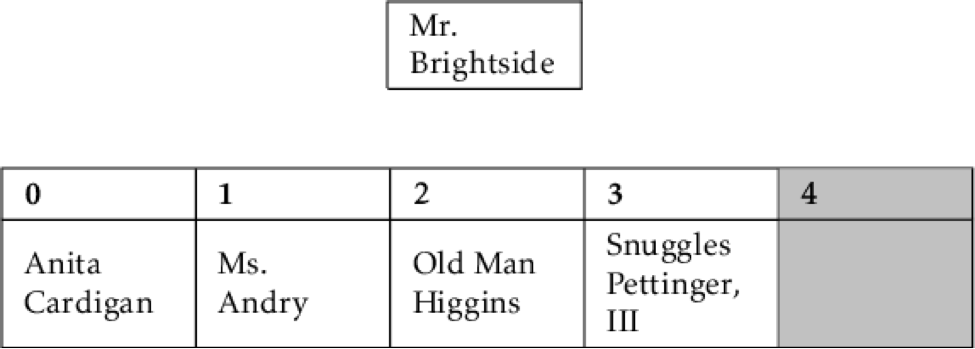
And before Ms. Andry (despite her protests about being pushed aside by a man).

 

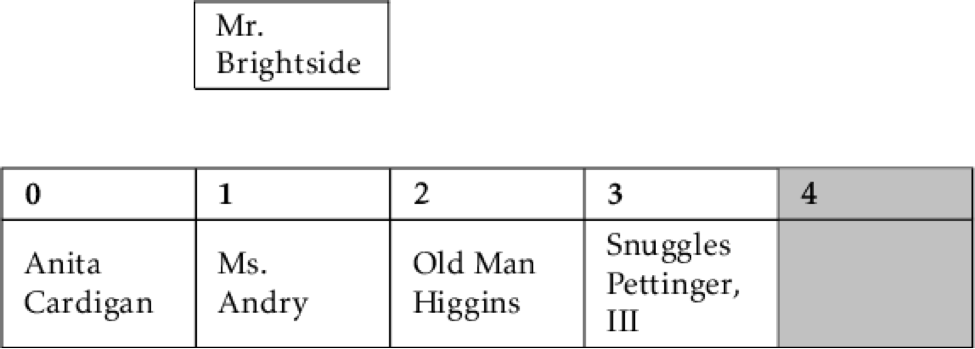
Until he's compared to Anita, who comes before him alphabetically. Every stuffed animal except Anita shifts to the right to make room for Mr. Brightside.

 

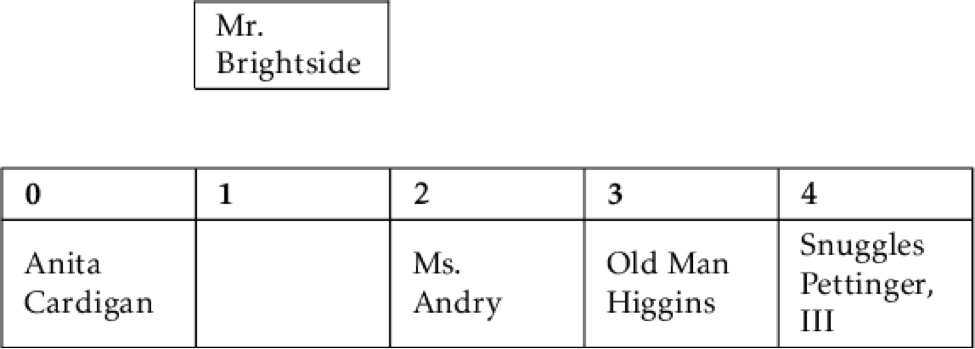
Then we insert Mr. Brightside and we're done.

 

The pseudocode for this algorithm looks something like this:

DEFINITION InsertionSort(List L)
	LET N be the length of L
FOR i in range 0 to N:
	LET j equal i
	WHILE j > 0 and L[j – 1] > L[j]:
		SWAP L[j] and L[j – 1]
		j = j – 1
	END while
END for

In the worst case, this algorithm runs in O(n²) time, but for small amounts of data, it's actually faster than "more efficient" algorithms.

By small, we mean Ten Items or Less checkout lane small. Please don't try to sort your entire Pokémon collection using Insertion Sort.

Bonus: It doesn't take much memory to use.