Sorting Algorithms: Merge Sort
Sorting Algorithms: Merge Sort
Out of all the different sorts, one emerges above the rest. Merge Sort is the classic recursive sorting algorithm, which is easy to see because it's so easy to see. First it splits the list into smaller and smaller pieces, and then it starts merging the pieces in order to sort elements.
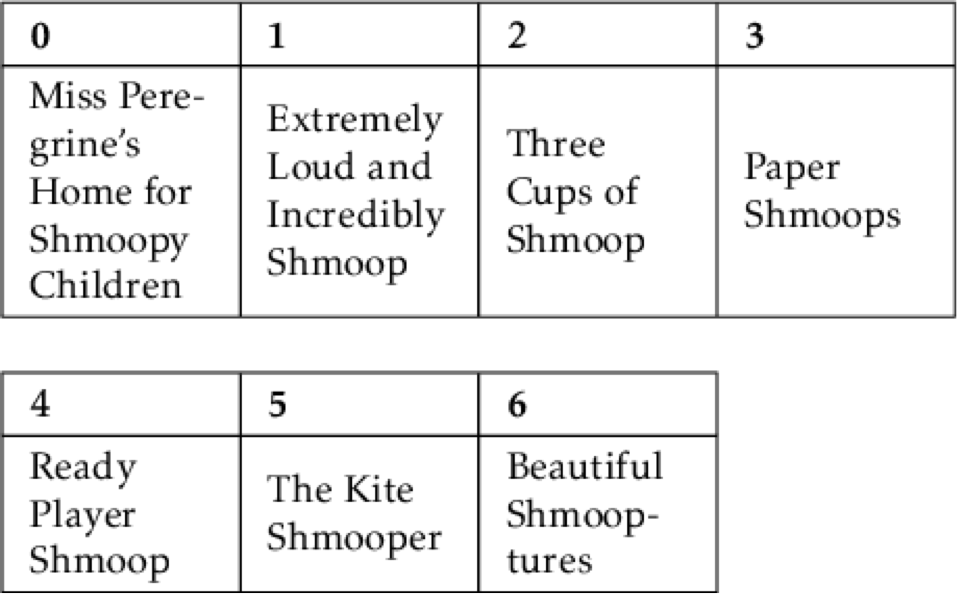
Say you have seven books you'd like to sort alphabetically by title.
Here are the books:
- Miss Peregrine's Home for Shmoopy Children
- Extremely Loud and Incredibly Shmoop
- Three Cups of Shmoop
- Paper Shmoops
- Ready Player Shmoop
- The Kite Shmooper
- Beautiful Shmooptures

…What? Computer scientists are allowed to love Teen Paranormal Romance just like anyone else. Beautiful Shmooptures is hauntingly tragic.
Okay, back to the sort.
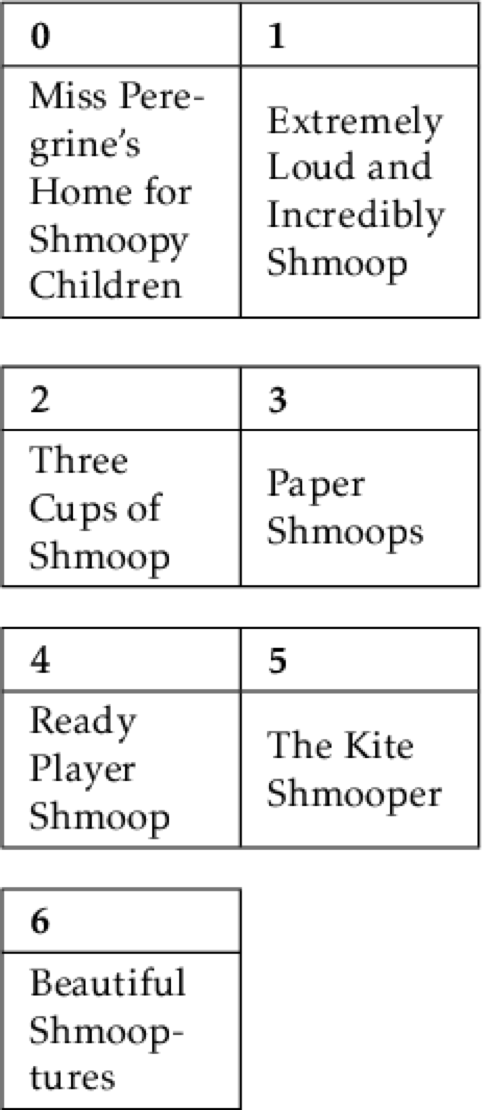
This algorithm divides and conquers by splitting the list in half.
Then it splits each half in half.
Aaaaaand, we split everything (that can be split) in half.
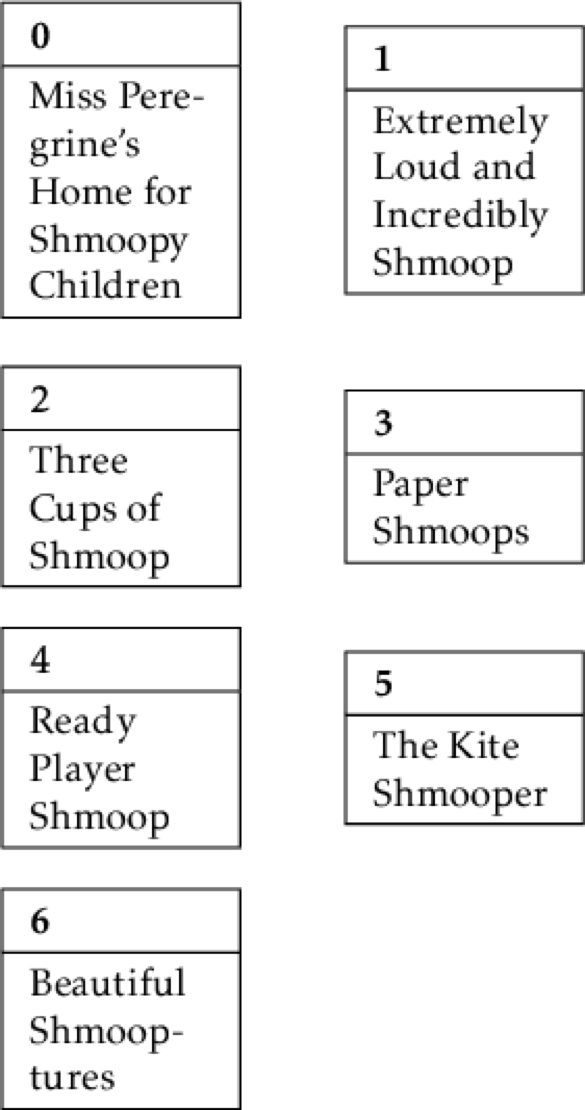
Now that we've split everything that can be split, it's time to start making comparisons between items. In their lists of one, every item is perfectly sorted, so we have to pair the lists and compare elements.

Since Extremely Loud and Incredibly Shmoop—a modern classic—comes before Miss Peregrine's Home for Shmoopy Children, we switch the two.

Through the magic of web tutorials, we've compared the rest of the pairs for you.
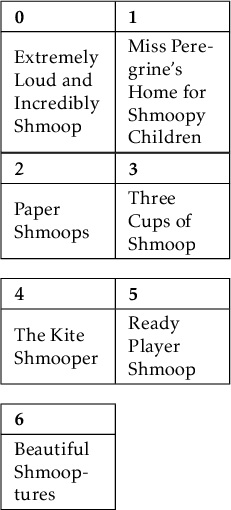
Let's get a little more ambitious and put two and two together, in this case 0 – 1 with 2 – 3. The trick is comparing the first book in each list, only moving to the next book if we can move that first element.
If we compare the first element of 0 – 1 with the first element of 2 – 3. The victor gets to go in the empty list of four elements.

Extremely Loud and Incredibly Shmoop comes before Paper Shmoops. We know it also comes before Three Cups of Shmoop without comparing them, so we stick Extremely Loud and Incredibly Shmoop as the book in the list. Now to compare Miss Peregrine against Paper Shmoops.

Since Paper Shmoops also comes before Miss Peregrine, we're left comparing an empty list against 2 – 3, so we can just stick them on the end.

Whelp, that's one list sorted. Let's sort 4-5 and 6:
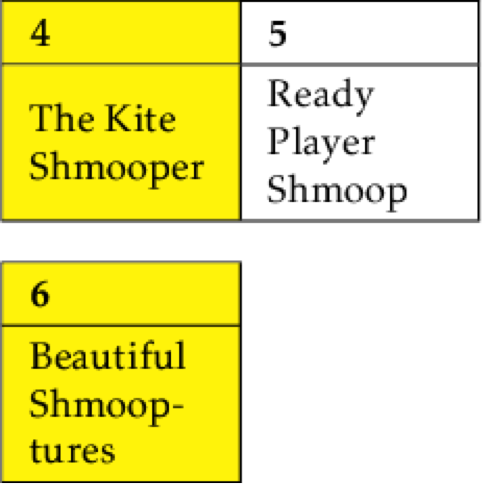
Since Beautiful Shmooptures comes before The Kite Shmooper, we can just stick it in front, knowing that it must also come before Ready Player Shmoop. This means that we need to re-index, so 6 becomes 4, 4 becomes 5, and 5 becomes 6.

Since both halves are sorted, we can compare them to each other, like so:

Keeping a marker on the first element of both lists, we compare to see which one comes first. Since Beautiful Shmooptures comes before Extremely Loud and Incredibly Shmoop, we add it to the list:

Then we remove it from the sublist and move The Kite Shmooper to the front.

If we were to ask a lonely old man which book came first alphabetically, he'd definitely say yes to Extremely Loud and Incredibly Shmoop.
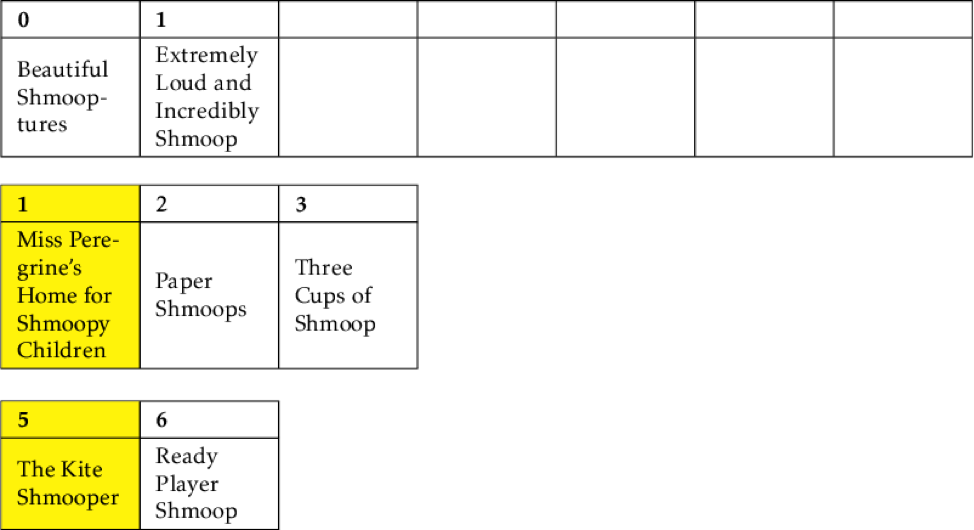
The Kite Shmooper comes before Miss Peregrine's Home for Shmoopy Children, and Miss Peregrine's Home for Shmoopy Children comes before Paper Shmoops, which comes before Ready Player Shmoop.

Ready Player Shmoop comes before Three Cups of Shmoop, completing the sorted list.

Because this divide-and-conquer algorithm splits every sublist in half and then compares the victors, it can sort the elements in O(nlogn) time.
Don't believe us? Check out the pseudocode.
FUNCTION MergeSort(List A): LET n be length(A) IF n equals 1: RETURN A
List B = A[0 : n ÷ 2] //the colon means that we're taking
//the range of values from the list
List C = A[ n ÷ 2 +1: n]
MergeSort(B) //since we've divided the list in half and called the function on
MergeSort(C) //both halves, the runtime of this part is 2logn
RETURN Merge(B, C)
END FUNCTION
FUNCTION Merge(List B, List C):
LET D be a List WHILE A and B have elements: //this loop makes the function linear
IF A[0] > B[0]:
ADD B[0] to the end of C
REMOVE B[0]
ELSE:
ADD A[0] to the end of C
REMOVE A[0]
END WHILE
WHILE A has elements:
ADD A[0] to the end of C
REMOVE A[0]
END WHILE
WHILE B has elements:
ADD B[0] to the end of C
REMOVE B[0]
END WHILE
RETURN C
END FUNCTION
From multiplying the runtime of the recursion and the loops, we know that Merge Sort runs in approximately nlogn time.
… That's really good for a comparison sort. As in, you can't do much better than nlogn.