Area, Volume, and Arc Length Introduction

Imagine that it's 2:15 in the morning. We're restless and surfing through television channels, when we come across an infomerical about the best knife set we'll ever have the opportunity to own. With just a phone call, we can own a knife set that will splice an atom for just 5 easy payments of $57.95. But if we call in the next 22 minutes and 37 seconds, we'll get the knife set and a dual mechanical backscratcher/hair dryer for only four easy payments of $57.95.

Now that we've bought all of this, we need a good use for the life-changing knife set. Lucky for us, we have a great use for them in calculus. In this chapter, we're going to learn to use knives to slice things up into little pieces. It's up to you to find something to do with that hairscratcher thing-a-ma-jig.

We already know how to cut the area under a function into slices that look more-or-less like rectangles:

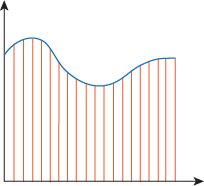
Just like we would slice a zucchini, we can chop any weird 3-D blob into tiny bits that look more-or-less like washers. He's not too happy about that:

If we make the slices small enough, we can break a curve into tiny bits that look more-or-less like straight lines:

After chopping our ambiguously shaped, angry blob–his name is Ornery–into tiny bits, we can find how much blob we get in each slice. No wonder he's not happy. He thinks we're going to eat him.

We'll learn that, by adding up all those bits, we can find his volume. Although there's nothing for Ornery to be afraid of, he's already warned his friend, Wily the wire. We're coming after him next.

While this chapter will help us hone our knife skills, this is not a chapter that will teach us to assemble a masterpiece of a dinner. We won't evaluate integrals ourselves. We will be set up to discuss bigger and better things than the area under a curve, though. With our new-found splicing skills, our imaginations are our only limits. We can begin drawing and understanding our own angry blobs, outraged areas, and crossed curves.

Happy hacking!