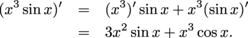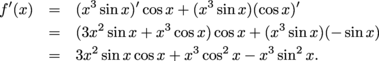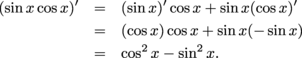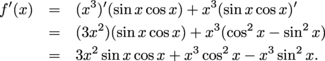Example 1
Let f(x) = x + 1 and g(x) = x.
- Find f ' (x).
Example 2
Let f(x) = x + 1 and g(x) = x.
- Find g ' (x).
Example 3
Let f(x) = x + 1 and g(x) = x.
- Find f ' (x) × g ' (x).
Example 4
Let f(x) = x + 1 and g(x) = x.
- Find (f × g)'(x).
Example 5
Let f(x) = x + 1 and g(x) = x.
- Must the derivative of the function f × g be equal to the product of f ' and g '?
Example 6
Find the derivative of the following function.
- f(x) = x sin x
Example 7
What's the derivative of f(x)?
- f(x) = excos x
Example 8
What's the derivative of the following function?
- f(x) = x ln x
Example 9
What's g ' (x) for the following function?
- g(x) = 5xex
Example 10
What's the derivative of g(x)?
- g(x) = (log2 x)(log3 x)
is a constant, therefore
Example 11
What's the derivative of g(x)?
- g(x) = 5ex
Example 12
Find the derivative of the following function.
- h(x) = (x2 + 2x)ln x
Example 13
What is h ' (x) for the following function?
- h(x) = ln x cos x
Example 14
Find the derivative of h(x).
Example 15
Find the derivative of j(x).
- j(x) = ln x + cos x
Example 16
What is the derivative of f(x) = (x2 + 2)(x3 – 4).
- Use the product rule.
Example 17
What's the derivative of f(x) = (x2 + 2)(x3– 4)?
- Rewrite f by multiplying the factors together, then take the derivative.
Example 18
- What's the derivative of
f(x) = x2exsin x
thinking of the function as
f(x) = (x2)(exsin x).
Example 19
Find the derivative of the function
f(x) = x3sin x cos x
in two different ways. Give the answer with everything multiplied out (instead of factoring out common factors).
