Collisions
Collisions in physics come in three flavors:
1. elastic collisions, where the kinetic energy of a system is conserved
2. inelastic collisions, where kinetic energy is not conserved
3. cherry
Okay, so two flavors. But the distinction between those two is important—what type of crash occurs in our problem determines what equations we can use to solve it.
The amount of kinetic energy lost as heat, sound, etc. in an inelastic collision is related to the coefficient of restitution (CR), a ratio of the speeds of two objects before and after impact. CR is always a number between 0 (maximum loss of kinetic energy, occurring when objects stick together after the collision) and 1 (no loss of kinetic energy—an elastic collision), and is given by:

Where the subscript "1'' indicates the first object, "2'' indicates the second, "i'' is the initial velocity before the collision, and "f'' is the final velocity after the collision.
In the case of both elastic and inelastic collisions, momentum is always conserved and becomes a useful tool for solving any problem dealing with collisions. For elastic collisions, our two conservation laws—momentum and energy—give us enough equations to solve for the velocities of both colliding objects.
Here's an example: two blocks, one weighing m1 and the other weighing m2, are sliding towards each other at v1,i and v2,i, respectively.
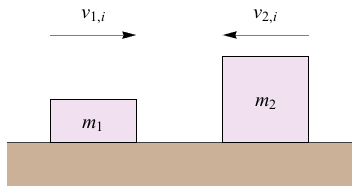
After the blocks collide, their masses don't change, but their velocities do, so that block 1 is now traveling at v1,f and block 2 at v2,f. Applying the laws of conservation of momentum and energy gives us this system of equations:
m1v1,i + m2v2,i = m1v1,f + m2v2,f

And solving these equations for v1,f and v2,f gives:

And if you thought that was a lot of algebra, well, you'd be right. Sorry about that.
Here’s another example: If Indiana Jones isn't quick enough the boulder will collide with him in an inelastic collision. Indiana Jones weighs mij and is running unsuccessfully away at vij,i. The boulder weighs mb and is rolling at a constant vb,i. If they collide, Indy sticks to the boulder, and thus their final velocities are the same at vf. Conservation of momentum gives us the following:
mijvij,i + mbvb,i = mijvf + mbvf
When you calculate total momentum, stationary objects contribute zero, but can gain momentum if they start moving. Velocity is directional, so sometimes v1 or v2 will be negative, and in order to calculate total momentum you must subtract. Two identical cars driving away from each other at the same speed, for example, have a net momentum of zero.
1. elastic collisions, where the kinetic energy of a system is conserved
2. inelastic collisions, where kinetic energy is not conserved
3. cherry
Okay, so two flavors. But the distinction between those two is important—what type of crash occurs in our problem determines what equations we can use to solve it.
The amount of kinetic energy lost as heat, sound, etc. in an inelastic collision is related to the coefficient of restitution (CR), a ratio of the speeds of two objects before and after impact. CR is always a number between 0 (maximum loss of kinetic energy, occurring when objects stick together after the collision) and 1 (no loss of kinetic energy—an elastic collision), and is given by:

Where the subscript "1'' indicates the first object, "2'' indicates the second, "i'' is the initial velocity before the collision, and "f'' is the final velocity after the collision.
In the case of both elastic and inelastic collisions, momentum is always conserved and becomes a useful tool for solving any problem dealing with collisions. For elastic collisions, our two conservation laws—momentum and energy—give us enough equations to solve for the velocities of both colliding objects.
Here's an example: two blocks, one weighing m1 and the other weighing m2, are sliding towards each other at v1,i and v2,i, respectively.

After the blocks collide, their masses don't change, but their velocities do, so that block 1 is now traveling at v1,f and block 2 at v2,f. Applying the laws of conservation of momentum and energy gives us this system of equations:
m1v1,i + m2v2,i = m1v1,f + m2v2,f

And solving these equations for v1,f and v2,f gives:

And if you thought that was a lot of algebra, well, you'd be right. Sorry about that.
Here’s another example: If Indiana Jones isn't quick enough the boulder will collide with him in an inelastic collision. Indiana Jones weighs mij and is running unsuccessfully away at vij,i. The boulder weighs mb and is rolling at a constant vb,i. If they collide, Indy sticks to the boulder, and thus their final velocities are the same at vf. Conservation of momentum gives us the following:
mijvij,i + mbvb,i = mijvf + mbvf
Common Mistakes
If an object is stationary, all of these formulas still apply—a stationary object just has a velocity of (you guessed it) zero.When you calculate total momentum, stationary objects contribute zero, but can gain momentum if they start moving. Velocity is directional, so sometimes v1 or v2 will be negative, and in order to calculate total momentum you must subtract. Two identical cars driving away from each other at the same speed, for example, have a net momentum of zero.