Conservation of Momentum
The universe, as you may have noticed by now, is a pretty cool place. Physics is really about unwrapping the universe and looking at the beauty underneath—and nowhere is that more evident than in the idea of conservation laws. There are certain quantities in the universe that were created with the Big Bang and cannot be destroyed, only converted from one form to another. Holiday fruitcakes are one.
Energy is another—stars like our sun are giant masses of nuclear potential energy. The sun beams that energy across the solar system to Earth. Plants absorb the energy. Animals eat the plants. Humans eat the animals (and the plants, too), and suddenly they have the energy to get out of bed. It's all the same energy that came from the sun, just in a different form. No more, no less.
Another example is momentum. Momentum is the product of an object's mass and velocity. It's conserved in the same way energy is—we can't create it or destroy it, only move it from object to object. This is the law of conservation of momentum.
In formula form:
p = mv
Here p is momentum (physicists aren't great at spelling, okay?), m is an object's mass, and v is its velocity. Momentum is measured in units of kg⋅m/s. Since it's the product of mass and velocity, momentum is much more than just an object's speed. It's a gauge of how much force has been given to an object, or how much force an object can transfer to something else. High velocity? Lots of momentum. Big mass? Also lots of momentum. It's how we can tell who the winner of a crash between a slow-moving semi-truck and a zippy Mini Cooper is going to be.
A useful way to see the law of conservation of momentum written involves some event that changes a bunch of objects' masses or velocities—say, a collision. (Or a diet.) For a collection of n objects:
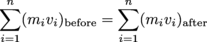
If you haven't seen the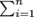
symbol before, don't panic. It just means a sum of n objects, starting from object 1. For n = 3, we could just as easily write (m1v1 + m2v2 + m3v3)before = (m1v1 + m2v2 + m3v3)after, but you can see how this could get out of hand fast with any bigger n. Physicists know the dangers of carpal tunnel. They're never going to write more than they have to.
If the collection of objects we're talking about are joined together—say, for example, a dumbbell, where the weights are so much heavier than the middle section that it's effectively two point masses joined together by a massless rod—we can often solve a problem by looking at the collection's center of mass. To find the center of mass of n objects, you take a weighted sum of each object and its position relative to the origin:
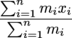
The denominator here works out to just be the total mass of the collection of objects.
The center of mass is always measured from somewhere (the "origin"), so it's important to remember where that somewhere is when trying to figure out a value for xi. We could want to know where the center of mass of our dumbbell is relative to the center (so the left weight would have a negative xi and the right weight a positive xi) or from the left side (so the left weight has xi = 0 and the right weight has a positive xi).
Center of mass is a useful tool, because when we consider a complex object's motion, we can look at the motion of its center of mass instead of having to worry about each individual part. It's like a cell phone—you don't have to memorize phone numbers; they're just stored in one spot: your address book. With the center of mass, we don't need to calculate every momentum for every part of an object—their behavior is stored in the center of mass.
Energy is another—stars like our sun are giant masses of nuclear potential energy. The sun beams that energy across the solar system to Earth. Plants absorb the energy. Animals eat the plants. Humans eat the animals (and the plants, too), and suddenly they have the energy to get out of bed. It's all the same energy that came from the sun, just in a different form. No more, no less.
Another example is momentum. Momentum is the product of an object's mass and velocity. It's conserved in the same way energy is—we can't create it or destroy it, only move it from object to object. This is the law of conservation of momentum.
In formula form:
p = mv
Here p is momentum (physicists aren't great at spelling, okay?), m is an object's mass, and v is its velocity. Momentum is measured in units of kg⋅m/s. Since it's the product of mass and velocity, momentum is much more than just an object's speed. It's a gauge of how much force has been given to an object, or how much force an object can transfer to something else. High velocity? Lots of momentum. Big mass? Also lots of momentum. It's how we can tell who the winner of a crash between a slow-moving semi-truck and a zippy Mini Cooper is going to be.
A useful way to see the law of conservation of momentum written involves some event that changes a bunch of objects' masses or velocities—say, a collision. (Or a diet.) For a collection of n objects:
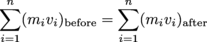
If you haven't seen the
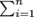symbol before, don't panic. It just means a sum of n objects, starting from object 1. For n = 3, we could just as easily write (m1v1 + m2v2 + m3v3)before = (m1v1 + m2v2 + m3v3)after, but you can see how this could get out of hand fast with any bigger n. Physicists know the dangers of carpal tunnel. They're never going to write more than they have to.If the collection of objects we're talking about are joined together—say, for example, a dumbbell, where the weights are so much heavier than the middle section that it's effectively two point masses joined together by a massless rod—we can often solve a problem by looking at the collection's center of mass. To find the center of mass of n objects, you take a weighted sum of each object and its position relative to the origin:
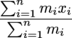
The denominator here works out to just be the total mass of the collection of objects.
The center of mass is always measured from somewhere (the "origin"), so it's important to remember where that somewhere is when trying to figure out a value for xi. We could want to know where the center of mass of our dumbbell is relative to the center (so the left weight would have a negative xi and the right weight a positive xi) or from the left side (so the left weight has xi = 0 and the right weight has a positive xi).
Center of mass is a useful tool, because when we consider a complex object's motion, we can look at the motion of its center of mass instead of having to worry about each individual part. It's like a cell phone—you don't have to memorize phone numbers; they're just stored in one spot: your address book. With the center of mass, we don't need to calculate every momentum for every part of an object—their behavior is stored in the center of mass.