Mirrors
Mirrors are odd creatures. We use them every day and we're never really surprised by what we see unless we happen to wake up to a particularly impressive case of bed head.
But when we look at mirrors with our physics eyes, they become both mysterious and surprising. We blame David Blaine. Left becomes right, right becomes left, up is still up, and down is still down. That's exactly what happens when looking at the bathroom wall through the mirrors. Don't get us started on all of those mirrors at the Circus' hall of mirrors.
Richard Feynman, physicist extraordinaire, said that at his MIT fraternity "hazing" included answering the question, "Why does left become right but up doesn't become down in your bathroom mirror?" This fraternity was not an Animal House.
But why do objects reflected by a mirror look like they are on the other side of the mirror?
Mirrors come in two flavors, plane and spherical. Plane mirrors are what we find in any bathroom or department store. All of the glass in the mirror is in the same plane—not in the Boeing 747 sense, but plane, as in the mathematical plane. Spherical mirrors don't bother with having all its reflective surface on the same plane.
This is because plane mirrors make the object distance, do, or the distance from Uncle Fester to the mirror, be equal to the image distance, di. The image distance is the distance from the mirror to the image of Fester. This generates a perfectly accurate version of Uncle Fester a distance, di, "behind" the mirror.
That mirrored Uncle Fester, a distance di behind the mirror, is considered a virtual image. Fortunately for him, there is no Uncle Fester clone trapped in the bathroom wall. No light rays pass through the mirror. If we place a piece of paper a distance di behind the mirror (behind the bathroom mirror and wall), we won't see the image projected onto that piece of paper.
How are virtual images created? We had better sharpen our pencils again, because it's time to unleash our inner artists once more.
Let's draw Uncle Fester in front of a mirror.
A way to guess what the image will look like is to imagine the line of the mirror as the spine of an open book. Imagine the Uncle Fester on the left as being freshly painted. If we slap the book closed on the painting and then re-open it, we have both the object and its "mirror image" of paint.
Now, let's add some mathematic rigor to this drawing.
Add a ray of light (red line) to your diagram coming from the bottom of Fester. Have it hit the mirror (blue line). Now remember our law of reflection, the incident angle, θi, is equal to the reflected angle, θr. The light ray reflects and hits our eye.
What our brain does is "fill in" a logical path for the reflected beam of light (dotted red line). It "extends" the reflected ray into the mirror. Our brains are way ahead of us – they knew light travels in a straight line before our physics textbooks ever told us. So our brain extends that light ray and places the origin of the extended ray at a distance, di, into the mirror:
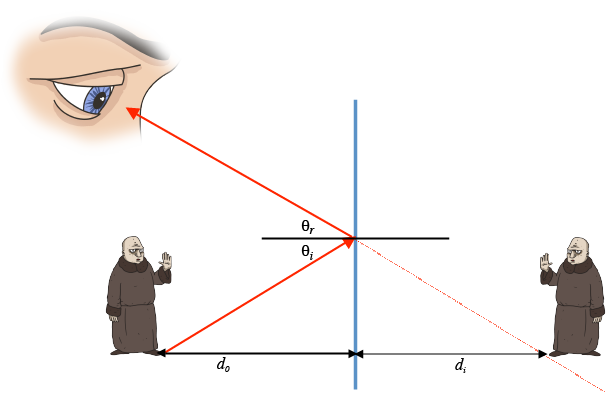
An easy way to draw this is to use a ruler to extend that red reflected light ray into the mirror. Then measure the distance between the bottom of the actual Uncle Fester and the mirror. This is the object distance, do. Since in a plane mirror, the virtual image will be placed the same distance into the mirror as the object is away from the mirror, we know that the bottom of Fester will be a distance di behind the mirror that is equal to do. So we take a ruler, place the line representing the mirror at 0 cm and then find at which point is the extended ray (the dotted red line in our diagram) a distance di from the mirror. That's where we place Uncle Fester's feet.
The same thing happens with light rays from the top of Fester's head. We'll draw those light rays in green, just to make things easier to tell apart:
We carefully reconstruct the image on the other side of the mirror:
The kind of drawing we just made is called a ray diagram. Each point is reflected to the other side, and while the real light path bounces off the mirror in between the point and the eye, it appears to come from behind the mirror at the intersection of the reflected distance and light path off of the mirror. This, lest we forget, is for plane mirrors only.
Technically, spherical mirrors don't have a focus. That is, incoming rays parallel to the axis will not all meet at a single point. A parabolic mirror on the other hand, will focus incoming rays parallel to the optical axis to a single point—you guessed it—the focus of the parabola. However, for incoming rays that are not too high up off the axis (compared to the radius of the mirror), a spherical mirror behaves very similarly to a parabolic mirror, focusing the light at a distance of half the radius from the vertex of the mirror. Since the geometry of a sphere is simpler, we'll use spherical mirrors for now and assume the height of all incoming rays is small compared to the radius of the mirror.
Concave, or converging mirrors, reflect parallel light rays in such a way that they all converge at a focal point, F, a focal distance, f, from the mirror.
We can calculate where the rays will converge using a very simple formula. Think of the concave mirror hugging the outside of a ball:
This ball, or circle, has a radius r. This radius is a measure of how curved the mirror is. The larger the radius, the less curved the mirror. Knowing the radius of curvature, r, of a mirror, we calculate the focal distance, f, using the formula f = r⁄2.
If we don't know the radius of curvature of our mirror, we can still determine the focal length of the mirror if we know the object and image distance. The mirror equation relates do and di to the focal distance, f, of a mirror as 1⁄do + 1⁄di = 1⁄f.
Mirrors can do all sort of crazy things. Some mirrors, such as shaving mirrors and make up mirrors, magnify or enlarge an image.
What is magnification? Optically speaking, it's how much bigger an image is than the object that produces it. We can use the image and object distance, or the image and object height, to figure out by how much something is magnified:
Note that negative sign in the equation with image distances to calculate the magnification factor. It's important, and here's why:
There are some sign conventions we have to follow. Any "real" object or image is positive:
(1) Object distance, do, and object height, ho, are always positive.
(2) Image distance, di, is positive for real images.
(3) Image heights, hi, is positive for real and virtual images that are
right side up.
(4) Image distance, di, is negative for virtual images.
(5) Image heights, hi, are negative for real and virtual images that are
upside down.
(6) Convex mirrors have a negative focal length, f.
(7) Concave mirrors have a positive focal length, f.
Some practice with ray diagrams and mirror equations will help these conventions feel like more than just conventions, they'll feel like they're there for a reason. A good way to remember the focal sign convention is that convex mirrors have their focal length behind the mirror, on the opposite side from the object, and therefore can only generate virtual images (with accompanying negative image distance).
The convention for the magnification equation is more intuitive than the distance ones. If the image is right side up (same direction as the object) then the image height and the magnification factor are both positive.
(1) An upside down image has a negative hi and magnification factor, m.
(2) A right side up image has a positive hi and magnification factor, m.
.We could then use additional information, such as the distance from the object to the mirror of 6 cm to calculate the image distance of -3 cm, from 
.Naturally, the distance from the mirror to the image isn't really a negative number, but it's in the negative direction and further indicates that this image is virtual. Real images have positive distances.
Back to our discussion.
Why do concave mirrors converge light rays? It seems like it would take a complicated explanation, but all we have to do is draw. (We're seeing a theme in this chapter.)
Let's draw four rays hitting a mirror. The mirror as a whole is curved, but each ray just sees the infinitesimal point of the mirror that it hits. We think of the particle nature of light for ray diagrams. Considering only a point, we refer to the law of reflection, that θi = θr. If each ray behaves as the law of refraction predicts, then the fact that the mirror is curved, causes the resulting rays to cross, or, in fancy Physics-language, converge. Here's a concave mirror with the addition of the normal to the surface and θi and θr for each ray:
So what do images look like in a converging mirror? It depends on where the object is relative to the mirror. Let's redraw our ray diagram including the concept of the mirror's radius of curvature.
If an object is more than the radius of curvature, or r, away from the mirror, we say it's beyond the center of curvature, C. When objects are beyond the center of curvature, the image produced is real, but smaller than the actual image.
Don't memorize these facts for the exams: a ray diagram will do the trick. Here's how.
Let's draw a heart in front of a concave mirror. Instead of drawing one light ray coming from the top and one from the bottom of the heart, lets draw two rays coming from the top. Additional rays identify the point of convergence for the image.
Now, follow these four steps:
In other words, the three rays to draw are as follows:
From the ray diagram, we can see a real image because the light rays pass through the image instead of only appearing to do so. This real image is smaller than the actual image, so magnification is less than 1.
Answer: Oh, goody. We get to use
with do = 6 cm and di = 8 cm, which leads to f = 3.4 cm. That means that the radius is twice from f, r = 2f = 6.8 cm.
We might answer a follow-up question the magnification of the image, which is m = -
.This isn't the kind of magnification we saw in the ray diagram above, but then again, that object was at a distance greater than the center and this object isn't: it's at 6 cm with the radius of 6.8 cm.
Let's draw a ray diagram for an object between the center of curvature, C, and the focal point, F. We follow the same three steps as in the last example:
This real image is upside down and has a magnification greater than 1.
See? No need to memorize or tattoo anything. As long as we remember the three ray paths to draw, we can figure out what concave mirrors do and when they do it.
Okay, now let's do the same thing for an object placed between the focal point and the mirror. Same three rays:
One ray can't go from the top of the heart through the focal point before it hits the mirror. Instead, it goes from the focal point to the top of the heart to get to the mirror. We just use the ruler to follow the line from F and the top of the heart, and then head out parallel as usual. The three light rays do not converge, but don't panic, it's natural. They converge if we extend their reflection lines behind the mirror. What happens instead is that a virtual image forms on the other side of the mirror, right side up and with a magnification over 1. We demonstrate the extension of the rays below using dotted lines to lead to the virtual image:
What have we learned from our three positions of objects with respect to a concave mirror? The image depends on where the object stands relative to its focal point and center of curvature. A great way to see this is to find a shaving mirror or makeup mirror. Those are the mirrors for closeups. When we're far away from the mirror beyond its center of curvature, we appear smaller and upside down (a real image). As we move closer to the mirror, within the center of curvature but beyond the focus, the image enlarges but remains upside down. Within the focus distance, however, suddenly the mirror does what it is supposed to do: we see a right side up enlargement. This example works with spoons, too.
While in front of the mirror with a magnified, right side up version of ourselves, move backwards until the image flips to upside down. That's the focal point of the mirror, F, and we can measure the distance, f, from the center of the mirror to our eyeballs. We could now use the equation relating the focal distance to the radius of curvature of a mirror (f =
,We could check this by looking for the point at which the upside down image has a magnification of 1 as we continue to move back away from the mirror.
Let's investigate the reasons behind the inevitable virtual image from a convex mirror. The focal point, F, of these mirrors is a virtual focal point—it is "inside" or behind the mirror on the concave side. There's no way to place an object on the same side of mirror as the focal point let alone between the focal point and the mirror as we did for the concave mirror.
For one of the exercises in this section, we'll use ray diagrams to determine whether convex mirrors generate enlarged or smaller images. For now, let's practice calculating.
Question: A department store has a large convex mirror installed up against the ceiling as a security measure, with a focal length of 20 cm. Where does the image appear for a person standing some 1.5 m away from it?
First, a convex mirror has a negative focal length, -0.2 m in SI units. The object distance is a positive 1.5 m. We use
to solve for 
and then since f is negative, we add those two terms together and ultimately find di = -0.176 m, or -17.6 cm, meaning it's near the focus on the opposite side of the mirror from the object, as is typical for virtual images. That seems about right, but we verify with a ray diagram, just to make sure.
But when we look at mirrors with our physics eyes, they become both mysterious and surprising. We blame David Blaine. Left becomes right, right becomes left, up is still up, and down is still down. That's exactly what happens when looking at the bathroom wall through the mirrors. Don't get us started on all of those mirrors at the Circus' hall of mirrors.
Richard Feynman, physicist extraordinaire, said that at his MIT fraternity "hazing" included answering the question, "Why does left become right but up doesn't become down in your bathroom mirror?" This fraternity was not an Animal House.
But why do objects reflected by a mirror look like they are on the other side of the mirror?
Mirrors come in two flavors, plane and spherical. Plane mirrors are what we find in any bathroom or department store. All of the glass in the mirror is in the same plane—not in the Boeing 747 sense, but plane, as in the mathematical plane. Spherical mirrors don't bother with having all its reflective surface on the same plane.
Plane Mirrors
Since plane mirrors are perfectly flat, they generate a perfect image of whatever is standing in front of them. By "perfect image," we don't mean that Uncle Fester ends up looking like Channing Tatum. By "perfect image," we mean that, unfortunately, a plane mirror does not lie. Uncle Fester looks like Uncle Fester: no taller, no shorter, and unfortunately, not even a smidgeon better looking.This is because plane mirrors make the object distance, do, or the distance from Uncle Fester to the mirror, be equal to the image distance, di. The image distance is the distance from the mirror to the image of Fester. This generates a perfectly accurate version of Uncle Fester a distance, di, "behind" the mirror.
That mirrored Uncle Fester, a distance di behind the mirror, is considered a virtual image. Fortunately for him, there is no Uncle Fester clone trapped in the bathroom wall. No light rays pass through the mirror. If we place a piece of paper a distance di behind the mirror (behind the bathroom mirror and wall), we won't see the image projected onto that piece of paper.
How are virtual images created? We had better sharpen our pencils again, because it's time to unleash our inner artists once more.
Let's draw Uncle Fester in front of a mirror.
A way to guess what the image will look like is to imagine the line of the mirror as the spine of an open book. Imagine the Uncle Fester on the left as being freshly painted. If we slap the book closed on the painting and then re-open it, we have both the object and its "mirror image" of paint.
Now, let's add some mathematic rigor to this drawing.
Add a ray of light (red line) to your diagram coming from the bottom of Fester. Have it hit the mirror (blue line). Now remember our law of reflection, the incident angle, θi, is equal to the reflected angle, θr. The light ray reflects and hits our eye.
What our brain does is "fill in" a logical path for the reflected beam of light (dotted red line). It "extends" the reflected ray into the mirror. Our brains are way ahead of us – they knew light travels in a straight line before our physics textbooks ever told us. So our brain extends that light ray and places the origin of the extended ray at a distance, di, into the mirror:
An easy way to draw this is to use a ruler to extend that red reflected light ray into the mirror. Then measure the distance between the bottom of the actual Uncle Fester and the mirror. This is the object distance, do. Since in a plane mirror, the virtual image will be placed the same distance into the mirror as the object is away from the mirror, we know that the bottom of Fester will be a distance di behind the mirror that is equal to do. So we take a ruler, place the line representing the mirror at 0 cm and then find at which point is the extended ray (the dotted red line in our diagram) a distance di from the mirror. That's where we place Uncle Fester's feet.
The same thing happens with light rays from the top of Fester's head. We'll draw those light rays in green, just to make things easier to tell apart:
We carefully reconstruct the image on the other side of the mirror:
The kind of drawing we just made is called a ray diagram. Each point is reflected to the other side, and while the real light path bounces off the mirror in between the point and the eye, it appears to come from behind the mirror at the intersection of the reflected distance and light path off of the mirror. This, lest we forget, is for plane mirrors only.
Common Mistakes
Drill it in: planar mirrors do not and never will create real images, only virtual ones.Brain Snack
(Planar) Mirrors are a hot topic of conversation in literature and pop culture, too. Check out Sylvia Plath's Mirror, Michael Jackson's Man in the Mirror, and the mirror in The Lady of Shalott. We could go on and on.Concave, Spherical Mirrors
Mirrors don't have to be flat, like the Circus' Hall of Mirrors' mirrors (which may improve Uncle Fester's appearance). The most common non-plane mirrors are spherical mirrors, shaped like a bowl with the reflecting material on either the inside of the bowl or the outside. The simplest spherical mirrors are concave, where the mirror caves in, or convex, where the mirror bulges out.Technically, spherical mirrors don't have a focus. That is, incoming rays parallel to the axis will not all meet at a single point. A parabolic mirror on the other hand, will focus incoming rays parallel to the optical axis to a single point—you guessed it—the focus of the parabola. However, for incoming rays that are not too high up off the axis (compared to the radius of the mirror), a spherical mirror behaves very similarly to a parabolic mirror, focusing the light at a distance of half the radius from the vertex of the mirror. Since the geometry of a sphere is simpler, we'll use spherical mirrors for now and assume the height of all incoming rays is small compared to the radius of the mirror.
Concave, or converging mirrors, reflect parallel light rays in such a way that they all converge at a focal point, F, a focal distance, f, from the mirror.
We can calculate where the rays will converge using a very simple formula. Think of the concave mirror hugging the outside of a ball:
This ball, or circle, has a radius r. This radius is a measure of how curved the mirror is. The larger the radius, the less curved the mirror. Knowing the radius of curvature, r, of a mirror, we calculate the focal distance, f, using the formula f = r⁄2.
If we don't know the radius of curvature of our mirror, we can still determine the focal length of the mirror if we know the object and image distance. The mirror equation relates do and di to the focal distance, f, of a mirror as 1⁄do + 1⁄di = 1⁄f.
Mirrors can do all sort of crazy things. Some mirrors, such as shaving mirrors and make up mirrors, magnify or enlarge an image.
What is magnification? Optically speaking, it's how much bigger an image is than the object that produces it. We can use the image and object distance, or the image and object height, to figure out by how much something is magnified:
Note that negative sign in the equation with image distances to calculate the magnification factor. It's important, and here's why:
There are some sign conventions we have to follow. Any "real" object or image is positive:
(1) Object distance, do, and object height, ho, are always positive.
(2) Image distance, di, is positive for real images.
(3) Image heights, hi, is positive for real and virtual images that are
right side up.
(4) Image distance, di, is negative for virtual images.
(5) Image heights, hi, are negative for real and virtual images that are
upside down.
(6) Convex mirrors have a negative focal length, f.
(7) Concave mirrors have a positive focal length, f.
Some practice with ray diagrams and mirror equations will help these conventions feel like more than just conventions, they'll feel like they're there for a reason. A good way to remember the focal sign convention is that convex mirrors have their focal length behind the mirror, on the opposite side from the object, and therefore can only generate virtual images (with accompanying negative image distance).
The convention for the magnification equation is more intuitive than the distance ones. If the image is right side up (same direction as the object) then the image height and the magnification factor are both positive.
(1) An upside down image has a negative hi and magnification factor, m.
(2) A right side up image has a positive hi and magnification factor, m.
Math Attack
What's the magnification of a 2 cm object off a spherical lens if the image is 1 cm and in the opposite direction? Answer: -0.5, from.We could then use additional information, such as the distance from the object to the mirror of 6 cm to calculate the image distance of -3 cm, from .Naturally, the distance from the mirror to the image isn't really a negative number, but it's in the negative direction and further indicates that this image is virtual. Real images have positive distances.Back to our discussion.
Why do concave mirrors converge light rays? It seems like it would take a complicated explanation, but all we have to do is draw. (We're seeing a theme in this chapter.)
Let's draw four rays hitting a mirror. The mirror as a whole is curved, but each ray just sees the infinitesimal point of the mirror that it hits. We think of the particle nature of light for ray diagrams. Considering only a point, we refer to the law of reflection, that θi = θr. If each ray behaves as the law of refraction predicts, then the fact that the mirror is curved, causes the resulting rays to cross, or, in fancy Physics-language, converge. Here's a concave mirror with the addition of the normal to the surface and θi and θr for each ray:
So what do images look like in a converging mirror? It depends on where the object is relative to the mirror. Let's redraw our ray diagram including the concept of the mirror's radius of curvature.
If an object is more than the radius of curvature, or r, away from the mirror, we say it's beyond the center of curvature, C. When objects are beyond the center of curvature, the image produced is real, but smaller than the actual image.
Don't memorize these facts for the exams: a ray diagram will do the trick. Here's how.
Let's draw a heart in front of a concave mirror. Instead of drawing one light ray coming from the top and one from the bottom of the heart, lets draw two rays coming from the top. Additional rays identify the point of convergence for the image.
Now, follow these four steps:
- Draw one ray that runs parallel to the optical axis (black line) that reflects off of the mirror and passes through the focal point, F, of the mirror.
- Draw a second line that goes through the focal point, F, before it hits the mirror and then is reflected so that it returns parallel to the optical axis.
- The top of the "image" heart is where the two reflected rays cross.
- Add a third line from the top of the object through the center, C, which is reflected straight back on itself (definition of a radius is that it's perpendicular to the edge of the circle).
In other words, the three rays to draw are as follows:
- In parallel, out through focus
- In through focus, out parallel
- Straight through center (reflected back on itself)
From the ray diagram, we can see a real image because the light rays pass through the image instead of only appearing to do so. This real image is smaller than the actual image, so magnification is less than 1.
Another Math Attack!
Question: What is the focal length and radius for a concave mirror with an object 6 cm away from the center of the mirror and the image 8 cm away?Answer: Oh, goody. We get to use
with do = 6 cm and di = 8 cm, which leads to f = 3.4 cm. That means that the radius is twice from f, r = 2f = 6.8 cm. We might answer a follow-up question the magnification of the image, which is m = -
.This isn't the kind of magnification we saw in the ray diagram above, but then again, that object was at a distance greater than the center and this object isn't: it's at 6 cm with the radius of 6.8 cm. Let's draw a ray diagram for an object between the center of curvature, C, and the focal point, F. We follow the same three steps as in the last example:
- In parallel, out through focus
- In through focus, out parallel
- Straight through center (reflected back on itself)
This real image is upside down and has a magnification greater than 1.
See? No need to memorize or tattoo anything. As long as we remember the three ray paths to draw, we can figure out what concave mirrors do and when they do it.
Okay, now let's do the same thing for an object placed between the focal point and the mirror. Same three rays:
One ray can't go from the top of the heart through the focal point before it hits the mirror. Instead, it goes from the focal point to the top of the heart to get to the mirror. We just use the ruler to follow the line from F and the top of the heart, and then head out parallel as usual. The three light rays do not converge, but don't panic, it's natural. They converge if we extend their reflection lines behind the mirror. What happens instead is that a virtual image forms on the other side of the mirror, right side up and with a magnification over 1. We demonstrate the extension of the rays below using dotted lines to lead to the virtual image:
What have we learned from our three positions of objects with respect to a concave mirror? The image depends on where the object stands relative to its focal point and center of curvature. A great way to see this is to find a shaving mirror or makeup mirror. Those are the mirrors for closeups. When we're far away from the mirror beyond its center of curvature, we appear smaller and upside down (a real image). As we move closer to the mirror, within the center of curvature but beyond the focus, the image enlarges but remains upside down. Within the focus distance, however, suddenly the mirror does what it is supposed to do: we see a right side up enlargement. This example works with spoons, too.
DIY Lab
Let's use a tape measure to determine the radius of curvature of a shaving mirror.While in front of the mirror with a magnified, right side up version of ourselves, move backwards until the image flips to upside down. That's the focal point of the mirror, F, and we can measure the distance, f, from the center of the mirror to our eyeballs. We could now use the equation relating the focal distance to the radius of curvature of a mirror (f =
,We could check this by looking for the point at which the upside down image has a magnification of 1 as we continue to move back away from the mirror. Convex, Spherical Mirrors
The last kind of mirror we need to talk about is a spherical, convex mirror. Convex mirrors generate only one type of image: a right side up, virtual image. For the record, though, saying "right side up, virtual image" is redundant because all virtual images are right side up.Let's investigate the reasons behind the inevitable virtual image from a convex mirror. The focal point, F, of these mirrors is a virtual focal point—it is "inside" or behind the mirror on the concave side. There's no way to place an object on the same side of mirror as the focal point let alone between the focal point and the mirror as we did for the concave mirror.
For one of the exercises in this section, we'll use ray diagrams to determine whether convex mirrors generate enlarged or smaller images. For now, let's practice calculating.
Question: A department store has a large convex mirror installed up against the ceiling as a security measure, with a focal length of 20 cm. Where does the image appear for a person standing some 1.5 m away from it?
First, a convex mirror has a negative focal length, -0.2 m in SI units. The object distance is a positive 1.5 m. We use
to solve for and then since f is negative, we add those two terms together and ultimately find di = -0.176 m, or -17.6 cm, meaning it's near the focus on the opposite side of the mirror from the object, as is typical for virtual images. That seems about right, but we verify with a ray diagram, just to make sure.Common Mistakes
Check those signs on distances and focal lengths before making any calculations: one misstep and wonky answers result. Use a ray diagram to double check the results. Then, for ray diagrams remember to draw the three rays because they're the same for any curved mirror (or lens, for that matter):- In parallel, out through focus
- In through focus, out parallel
- Straight through Center (reflected back on itself)