It's a Particle. Wait. It's a Wave.

In Newton's time, life was simple for a physics student. Most scientists, including Newton, thought of light as a particle, a kind of stream of tiny ping-pong balls that bounces off some objects, but travels through others. That behavior would obey Newton's laws of mechanics, and life was good.

Light is as wavy as Huygen's hair.

(Source)

But then along came a group of physicists, including one named Huygens, who decided to complicate the model. They pointed out that the classical view of light (called geometric optics) couldn't explain things like refraction and interference. To explain these phenomena, Huygens suggested that light is not a particle, but a wave.

Huygens did not stop there. Huygens' Principle says that each wave front is made up of an infinite number of points, and each point is a source for a new wave, or wavelet if you will. This is how Huygens said light propagates.

Time for a diagram.

In the diagram below, the red line is a wave front at an early time point. We're only drawing 5 blue dots to represent the infinite number of points because, well, an infinite number of blue dots on a page isn't practical. The new wavelets are shown here as thin blue waves propagating from each blue dot. The new wave front (purple line), at a later time, results from the addition of all of the little wave fronts.

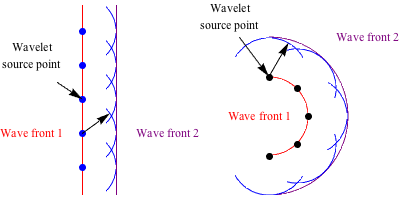
Wavelets at one end of a wave front can do things independently of the wavelets at the other end of the wave front. If the bottom of a wave front hits an object and gets bent around that object, or diffracted around that object, that part of the wave front is bent while the rest of the wave front continues on its original path.

Huygens' Principle also explains why light refracts, or bends as light passes through a different material.

Let's see how Huygens explains refraction. Sharpen that pencil: it's time to draw.

1. Draw a light ray (red arrow) that travels through air and hits a plastic box. Don't forget to draw the normal, for measuring angles (The normal is a line perpendicular to the surface of the object). In this case, let's say that the light is refracted, or bent, towards the normal as it passes from material 1 to 2.

Now's a good time to introduce a new term we need, index of refraction, n. We call the ratio between the speed of light in a vacuum and the speed of light in a medium the index of refraction, n. Different objects, or mediums, have different indices of refraction because light travels more slowly in some things than in others, hence the bending of light.

2. To start thinking about refraction in wave terms, draw in the wave front (green lineperpendicular to the direction of light's travel) before it has reached the object, material 2.

3. So far, so good. What happens when part of the wave front enters the object? Remember, when light moves from one medium to another it changes not only direction but also speed, so the part of the wave in the plastic box will travel at a different speed than the rest of the wave that is still traveling through air.

How much slower the part of the wave in plastic is (contributing to the change in angle) depends on the difference in optical density, or refractive indices, of the two objects. In our diagram light is being bent towards the normal, so θ₂ < θ₁. According to Snell's law, n₁sinθ₁, = n₂sinθ₂, if θ₂ < θ₁,then n₂ has to be bigger than n₁.

Again, the refractive index, n, is a measure of how much slower light travels in an object than it would in a vacuum, or .In this equation, c is the speed of light in a vacuum, which is constant. A large n-valuemeans that v, the speed of light in the object, is small. Since for our diagram we established that the refractive index of the object the light is traveling into, n₂, is greater than that of the medium it was traveling in before, we know that the velocity, v₂, in the object is slower. In plain old English: light slows down when it hits the plastic box.

Let's add a second green line to our diagram to illustrate this.

Light slows down in the plastic, so that part of the wave front moves more slowly than the parts that are still traveling through air, and, voilà! Our perfectly straight green wave bends. This is possible because a wave front is made up of many point sources of little wavelets that can act independently of each other.

Let's add a second green line to our diagram to illustrate this.

Light slows down in the plastic, so that part of the wave front moves more slowly than the parts that are still traveling through air, and, voilà! Our perfectly straight green wave bends. This is possible because a wave front is made up of many point sources of little wavelets that can act independently of each other.

The slowing of light as it hits the plastic block means that light is refracted. In this case, because light is slowing down, it bends towards the normal.

We can visualize refraction by using a laser pointer and shining it at an angle through all sorts of translucent materials so we can see how the angle changes from air into the object, and again back out. We could even determine the index of refraction of each material by taking angle measurements with respect to the normal.

Let's practice the math now. If n₁ = 1.3 for ice and n₂ = 1 for air (close enough to a vacuum) and the angle at which the light beam travels through the ice is 65˚ with respect the surface of the ice cube, at what angle does it travel through air? Answer: first we need the angle with respect to the normal, which is 35˚. Then we calculate θ₂ = arcsin (1.3 sin 35) = 48.2˚.

Common Mistakes

Whole tables of indices of refraction exist for all sorts of materials. If in doubt, check a table.

Brain Snack

Incidentally, a prism refracts white light into all its constituent colors because different wavelengths (colors) of light refract by different amounts

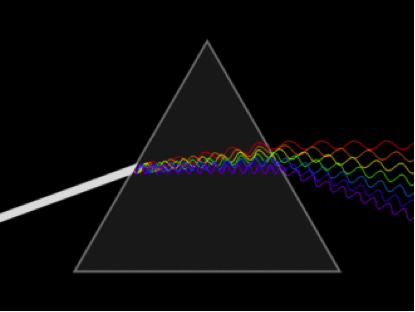
(Source)