Graph y = x³ – 5x² – 8x + 12.

First we need to find the factors for this polynomial. Using the Remainder Theorem, we'll focus on the factors of the constant 12: ±12, ±6, ±4, ±3, ±2, and ±1.

At Shmoop, we follow the KISS principle whenever possible: Keep It Simple, Shmooper. Nothing is simpler than plugging in a 1.

P(1) = (1)³ – 5(1)² – 8(1) + 12

= 1 – 5 – 8 + 12

= 0

Another success for KISS: x – 1 is one of the factors. We're so happy, we could KISS you.

Now we'll use this 1 in our synthetic division to find the other factors.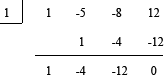

The whole polynomial factors to:

P(x) = (x – 1)(x² – 4x – 12)

= (x – 1)(x – 6)(x + 2)

Solve for the roots:

x – 1 = 0, x – 6 = 0, or x + 2 = 0

Our roots are x = 1, 6, and -2.

Plot those zeros on the graph, so we can see what sections we need to investigate further.

This polynomial is covered in third-degree burns, which is ironic because it has a degree of 3. As we take it to the hospital for treatment, we notice that its end behavior has one end pointing up and the other down.

Now we're going to find one ordered pair in each section of the graph to find the general shape. These aren't the only numbers that will work, so feel free to find your own. You won't hurt our feelings.

P(-3) = (-3)³ – 5(-3)² – 8(-3) + 12 = -36 → (-3, -36)

P(0) = (0)³ – 5(0)² – 8(0) + 12 = 12 → (0, 12)

P(3) = (3)³ – 5(3)² – 8(3) + 12 = -30 → (3, -30)

P(7) = (7)³ – 5(7)² – 8(7) + 12 = 54 → (7, 54)

Plot! Visualize! Enhance!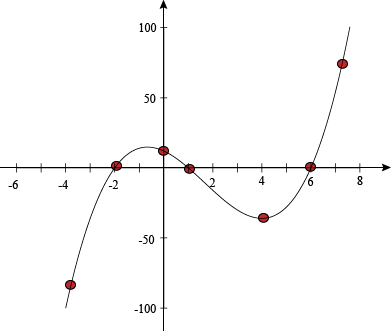

Graph y = x³ + 2x² – 5x – 6.

We start off our graphing by finding all the spots where it touches the x-axis. That means the roots, and that means we need to find the polynomial's factors.

Possible factors are x ±6, ±3, ±2, and ±1.

KISS with 1:

P(1) = (1)³ + 2(1)² – 5(1) – 6

= 1 + 2 – 5 – 6

= -8

KISSing didn't work this time. Welp, moving on. Let's try 2.

P(2) = (2)³ + 2(2)² – 5(2) – 6

= 8 + 8 – 10 – 6

= 0

Sweet; x – 2 is a factor, so now we can use synthetic division to find the others.

We have x² + 4x + 3 as the other factor of the polynomial. It can be factored further to find more roots.

P(x) = (x – 2)(x + 1)(x + 3)

Setting each part equal to 0 gets us roots of x = 2, -1, and -3.

Our graph will touch the x-axis at these three points.

The degree is odd, so our graph should have one end pointing up and the other down.

We need a few more values to finish off the graph.

P(-4) = (-4)³ + 2(-4)² – 5(-4) – 6 = -18 → (-4, -18)

P(-2) = (-2)³ + 2(-2)² – 5(-2) – 6 = 4 → (-2, 4)

P(0) = (0)³ + 2(0)² – 5(0) – 6 = -6 → (0, -6)

P(3) = (3)³ + 2(3)² – 5(3) – 6 = 24 → (3, 24)

Graph time.

Success.

Graph f(x) = x³ – 9x² – 12x + 20.

Time to go hunting for roots: under bushes, on potatoes, and among the factors of 20. They are ±20, ±10, ±5, ±4, ±2, and ±1.

f(1) = (1)³ – 9(1)² – 12(1) + 20 = 0

Keep on keeping it simple. It pays off handsomely.

Now we'll use this 1 in our synthetic division.

This gives us a factored polynomial:

f(x) = (x – 1)(x² – 8x – 20)

= (x – 1)(x – 10)(x + 2)

This means our roots are:

x = 1, 10, and -2

Now we can get the general shape of the graph by plugging and chugging in some points from each section.

f(-3) = (-3)³ – 9(-3)² – 12(-3) + 20 = -36 → (-3, -52)

f(0) = (0)³ – 9(0)² – 12(0) + 20 = 20 → (0, 20)

f(5) = (5)³ – 9(5)² – 12(5) + 20 = -140 → (5, -140)

f(11) = (11)³ – 9(11)² – 12(11) + 20 = 130 → (11, 130)

Now to plot these points and connect them with a smooth curve.

A quick double-check of the end behavior shows that it goes up at one end and down at the other, just like an odd-degree polynomial should.

Graph y = -x³ + 2x² + 9x – 18.

We start again by using the Remainder Theorem to sniff out one of the roots. The factors of -18 are ±18, ±9, ±6, ±3, ±2, and ±1.

P(1) = -(1)³ + 2(1)² + 9(1) – 18

= -1 + 2 + 9 – 18

= -8

Nope, no rooty-toot here. Try 2.

P(2) = -(2)³ + 2(2)² + 9(2) – 18

= -8 + 8 + 18 – 18

= 0

Ah, there's a root at x = 2, so one of our factors is x – 2. Now to use synthetic division to root out (hah!) the other factors.

P(x) = (x – 2)(-x² + 9)

Factor out a -1 from -x² + 9 to make it easier to factor.

P(x) = -(x – 2)(x² – 9)

P(x) = -(x – 2)(x + 3)(x – 3)

Now we've got all our factors, allowing us to find the roots of the polynomial. Our guess is that they're underground, beneath the trunk.

The zeros are at x = 2, -3, and 3. The "-" sign out front doesn't have any effect on what the roots are at this point.

We have four sections to check out. After this problem, we'll be qualified to become a certified Section Inspector.

P(-4) = -(-4)³ + 2(-4)² + 9(-4) – 18 = 42 → (-4, 42)

P(0) = -(0)³ + 2(0)² + 9(0) – 18 = -18 → (0, -18)

P(2.5) = -(2.5)³ + 2(2.5)² + 9(2.5) – 18 = → (2.5, 1.375)

P(5) = = -(5)³ + 2(5)² + 9(5) – 18 = -48 → (5, -48)

Plot the points, connect the points, get the points, high score.

We can double-check that the end behavior on the graph is correct for this polynomial. The degree is odd, so one end points up and the other end points down, like a very bendy, very number-filled see-saw.