Dude, This Is Radical
Next stop, radical town. All aboard the root train. While en route, all food service will be suspended with the exception of simplifying square roots and imaginary numbers.
Okay, Shmoopers. We admit it. That was corny. And we know that you can't eat square roots or imaginary numbers. We were just getting tired of the radical surfer references. Regardless, this section is all about roots and radicals.
A radical is any expression that uses the √ symbol. Take ∛5, for instance. This is a radical expression. In this expression, 3 is technically called the index, √ is known as the radical symbol, and 5 is the radicand.
The next thing we need to know is how to simplify one of these so-called radicals. In other words, how to write a radical in what's otherwise known as simple radical form (more on that later). From there, our lovely sample problems will help us learn how to add, subtract, multiply, and divide roots. Enjoy the Shmooptastic ride.
Sample Problem
Simplify the following: 
.
This is just a bit of a warm-up. We're reminding you that more than just square roots do exist. This cube root is really asking the question: What number multiplied by itself 3 times is -216?
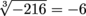
Nailed it. The answer's -6, because (-6)(-6)(-6) = -216.
Sample Problem
Simplify the following: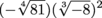 
.
This one's still pretty basic, despite there being a couple steps to navigate. First, let's evaluate these radicals in the parentheses.
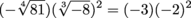
Next, we should follow our order of operations and square the negative 2.
(-3)(-2)2 = (-3)(4)
Lastly, let's multiply and move on with our lives.
(-3)(4) = -12
Sample Problem
Simplify the following: 
.
This problem isn't quite so easy;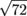 
doesn't simplify to some nice, neat whole number like 
did in the first sample problem. That means we need to break down the radical into simple radical form. To do this, we break down 
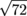into a product of prime numbers.
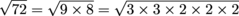
Once we have our prime number breakdown in the bag, we can start to simplify. Since √(3 × 3) = 3, we can pull a 3 out of the square root. Gee, we can pull out a 2 as well. This gives us…
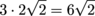
This is simple radical form. In other words, our radical now contains only a product of unique primes. The key idea to remember is that when you have a pair of primes, you can always pull one out.
Sample Problem
Simplify the following: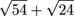 
.
This is a little bit tougher. Don't worry. We have you covered. All we really need to do is break down both square roots into their simple radical form.
Next, we're going to pull out our pairs.
By the way, if you get comfortable and go right from 
to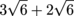 
, go for it. That just means that you're starting to truly understand, grasshopper.
Finally, since we've got two like terms, we can add them together. This might be confusing, but it's really no different than saying 3x + 2x = 5x. The difference here is that instead of x, we're using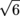 
.
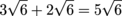
One final note: adding like terms such as this is only okay if the terms are really alike. You wouldn't add 
together, for the same reason you wouldn't add 3x + 2y together. Understand, rubber band?