Special Relativity
Einstein is one of the most famous, most intelligent, most splendiferous people to ever grace Earth, but he did poorly at the Polytechnic Institute in Zurich, Switzerland. Apparently, he only applied himself in subjects he cared about and couldn't care less about the rest of them. He was also critical of the educational system, which focused on well-established classical physics and ignored all revolutionary topics in modern physics brimming with excitement. As a result, professors thought Einstein disrespectful and didn't like him much.
Einstein worked in a patent office at the time he developed the theory of relativity. Constantly thinking about electromagnetic inventions might have contributed to the theory's development.
Everything in the universe is subject to electromagnetic forces. The only exception to this is gravity, which we'll chat about in just a bit. Light, as it turns out, also obeys the rules of electromagnetism. By the way, light also obeys the laws of gravity, but that's a topic left for general relativity, rather than the special relativity we're studying now.
It's time to apply some logic. The laws of electromagnetism can't change. That's why we call them "laws." Light obeys these laws, but (and this is a big but) the speed of light doesn't change by changing the frame of reference. Conclusion? The laws of physics don't depend on us, as the observers, or on our motion. In other words, there is no preferred frame of reference in which to do physics.
This exercise in logic is Einstein's first postulate for his theory of special relativity. It simply means that our frame of reference is not better than Gaspard's, Igor's, or the trashcan's for that matter.
It's a good thing Einstein wasn't around when Galileo got convicted. This first postulate pretty much insists Earth isn't special at all. The laws that formed our home planet are the same across the entire galaxy and beyond.
Einstein's second postulate is one we've already discussed. The speed of light is the same anytime, everywhere.
That's all there is to it, so why is it called Einstein's special theory of relativity? Most phenomena in the world can be described with electromagnetism, except for gravity. Gravity is a force causing acceleration, so the motion of objects under the influence of gravity can't be described with inertial frames.
Einstein's theory of relativity is special because it ignores acceleration. General relativity, on the hand, is generalized to include gravity.
Einstein didn't become a celebrity either in or out of the world of physics until his theory of relativity was verified experimentally in 1919. From then on, he became a household name.
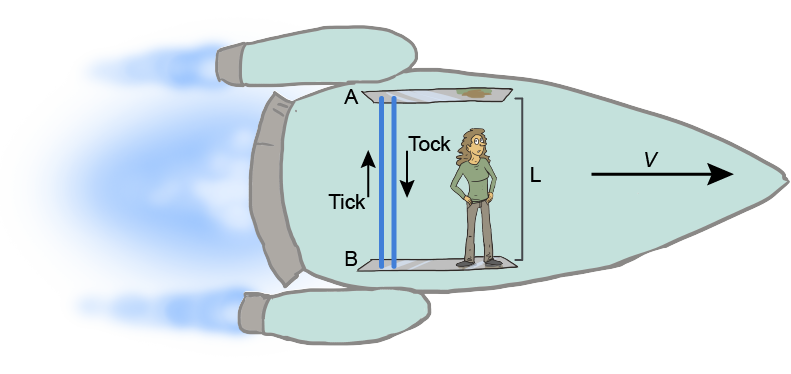
Imagine the following scenario. To escape Gaspard's wrath, we jump into a spaceship with a mirrored floor (B) and a mirrored ceiling (A), as you can see in the diagram below. Our ship, called The Albertian,travels with speed v and has a length L. The floor of the ship has a "light clock" that emits a beam of light from the floor to the ceiling (tick) and bounces back to the floor (tock). So in this scenario, an event is defined as "tick tock." Therefore, the light beam travels a distance of d = 2L during one single event.
We also know that time is distance over speed—even our speedometers are labeled in miles per hour. The speed in the spaceship clock is the speed of light, c. According to ourselves, within our frame of reference S', the entire time Δt' the beam of light takes to travel up and down between the two mirrors (the event) is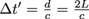
.We're using all primes for our frame of reference S', and an observer can have everything without primes for reference S.
Here comes an observer now. After we jumped into the spaceship, Gaspard pops up out of the bushes. To infuriate him even more, we bought the upscale model of The Albertian with windows so that he can see us out of his reach. Flabbergasted, he watches us zoom by at velocity v. We'll leave his enraged exclamations to imagination, where they belong. What does Gaspard see, apart from our triumphant grins as we wave him adieu?
A picture is worth a thousand words, especially Gaspard foaming with rage. Let's redraw the light clock from Gaspard's frame of reference S:
According to Gaspard, the light beam doesn't travel a distance d of 2L as it does in our own frame of reference. To him, the spaceship is moving, so the light bouncing between mirrors travels diagonally as the mirrors move with the spaceship as we can see in the diagram. To Gaspard,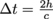
.The distance the spaceship moves during the event according to Gaspard we'll call displacement x. The time from the spaceship to move from A to C is the same time as Gaspard's event time. .
What's x? The Albertian is traveling at velocity v. Length or distance, as usual, is given by velocity multiplied by time, which in this reference S is x = vΔt.
And what's h? Yes, we need the hypotenuse of the right-angle triangle drawn above, with sides L and
, which is 
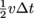when we substitute in x = vΔt. Now, we're set to find h, crosssing our fingers that we remember geometry.
Using Pythagoras' theorem, we know that
. We also know that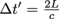 
, 
,and x = vΔt. Therefore, 
, and 
.Substituting in the first equation of this paragraph, we get 
. Solving for Δt in terms of Δt' doesn't take too long. Besides, we're itching to know how to relate the time from one frame of reference to another.
We define the fraction
as β (Beta), a ratio of a speed in terms of the speed of light. We can use it in 
to create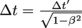 
Where there's one Greek letter, there's bound to be more. The quantity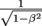
appears so often in relativity that it's a lot easier to rename it the relativistic factor and assign it another symbol, γ (gamma), such that 
.
The use of the relativisitic factor turns our derivation into Δt = γΔt'.
Ah, that's easier on the eye, and on the brain too. The time difference between one frame and another frame is calculable based solely on the speed between the two frames. That's because γ has the ratio of speed to the speed of light hiding inside β. Note that when β is near zero then γ = 1 and time is unchanged.
And that's how you can stop time.
Proper time is Δt' in the above equation and we often rewrite it as Δto (pronounced t-not, better understood as t-naught). Proper time is ourtime in this case, the time that we measure the light beam going "tick tock" while standing inside The Albertian. Think of proper time as the time in a frame of reference at rest, or the time according to something within the same frame of reference as the event.
Relativistic time, on the other hand, is the time Δt that Gaspard measures as he sees the light beam travel a diagonal path from A to C aboard our spaceship. If the light clock were down on Earth with him, he'd measure proper time and we'd measure relativistic time from aboard our space ship.
We can rewrite the equation we derived as Δt = γΔto. .
For the same event, we have two times: proper time and relativistic time. Time isn't a constant, like it seems to be for Gaspard and ourselves on the ground moving nowhere near the speed of light such that β = 0 and γ = 1 and all of Newtonian physics is true. On the other end of the speed spectrum, we know v can never be greater than c from Einstein's first postulate. This means that β < 1 and γ must always be larger than 1, so Δt > Δto, or the proper time is always the shortest measurable time.
For our now-familiar chase, Gaspard will measure the event (the tick-tock) as lasting longer than we will. One second for us is shorter than one second for Gaspard. In other words, time gets stretched out at relativistic speeds. This phenomenon is known as time dilation.
Let's say a particle zips through space at half the speed of light. By how much is its time dilated according to an observer on Earth? We'll be using Δt = γΔt'. We need to find γ first then, which depends in turn on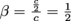
. When 
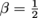, then 
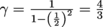.Earth time we'll call S, with particle time S'. Lastly we have 
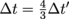. That's the dilated time according to earth. It's 
for the particle in terms of Earth time.
It shouldn't be that hard to decide whether or not two events occur at the same time, but only if we're within the same frame of reference. What if we raced Igor starting in the middle of the alley and we both ran in opposite directions with the same speed with two different finish lines the same distance from the starting point? Would we both cross the two finish lines at the same time according to everyone?
To answer this puzzling question, let's go back to your nocturnal escape aboard The Albertian. Unfortunately, our new state-of-the-art spaceship breaks down as we whiz past Gaspard in the darkness of the night. We're forced to improvise.
Our spaceship comes crashing back to earth at a merchandise train station. One of the wagon doors is wide open so we jump inside a cart of length L. There is nothing in the wagon but a small battery-operated lamp mounted on the center of the floor. Gaspard, having seen the spaceship crash, catches up just as the train takes off with a dashing relativistic velocity v. We want him to see our escape to rub it in so we flick on the light and proceed to smile and wave again.
What happens, according to you? Let's take a look at the drawing below:
As soon as we turn on the light positioned smack dab in the middle of the train car, two light beams shine from the center of the wagon and hit the two walls of the cart. Since light always travels at speed c, both light beams reach the two walls at exactly the same time. These two simultaneous events, according to ourselves, occur exactly 20 nanoseconds later than flicking on the light. If we assign our frame of reference the letter S', conveniently the same as before, then proper time Δto = 20 ns for a beam of light traveling at speed c to travel a distance equal to half the lengthof the wagon. We are using proper time Δto since we're in the same frame of reference as the light (event).
Now, let's look at what Gaspard sees as he shakes his fist at us.
Do both light beams reach the walls at the same time according to Gaspard?
The answer, as we've determined from the drawing, is no, or nein as our friend Einstein would say. Two events that were simultaneous in our frame of reference S' aren't simultaneous according to Gaspard's frame of reference S. It takes lessthan 20 ns for the left light beam to reach the wall, since the train is moving with velocity v so the back of the train moves towards the position from which the photon left the light fixtures, and morethan 20 ns for the right light beam to reach the other wall as that side of the train moves away from the position from which a different photon simultaneously left the light fixture.
In conclusion, two events that are simultaneous in one frame of reference aren't simultaneous in another if it's moving at a relativistic speed.
x' = x − vt
y' = y
z' = z
t' = t
These transformations assumed time was absolute as opposed to relative. We've also seen that time dilation occurs when speeds become a significant fraction of the speed of light. How do our Galilean transformations change when the relative velocity v of the two frames is relativistic, a significant fraction of the speed of light, c?
The derivation is left for you to do in Thoughts and Study questions. The resulting equations are called the Lorentz-Einstein transformations:
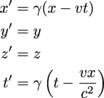
Remember that y and z don't change because v is exclusively in the x direction. We could easily rewrite these equations for objects moving in other directions, or define the x-direction as whatever direction the object in question travels. The x-coordinate is usually chosen because it eliminates height changes and varying an object's height would involve the force of gravity. This is chapter on special relativity, so gravity isn't welcome here.
From these, we may extract relativistic velocities ux and ux' in the same manner as we found Δt' in terms of Δt. We're spared the derivation—for now. The results are below.
At the risk, er certainty, of repeating ourselves, ux is the relativistic velocity of an object in frame of reference S, while ux' is the relativistic velocity in another frame of reference S'and v is the relativistic velocity between these two frames. There are some similarities to the time dilation equation we derived, but these velocity equations lack gamma.
The equations above are for finding the speed of one frame or the other. We can find the relative velocity between them by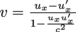
.
Oh, wait. We already did that, so now, let's turn our attention to length as measured in relativity. Since time changes in relativity, we had better expect the rest of space-time (the space part) to change, too.
A change in observed length is one of the consequences of multiple events occurring simultaneously in only one frame of reference.
One way of measuring the length of an object, say your (unopened) Jedi light saber, is to note both its ends on a ruler using the frame of reference S.
We could say that the frame of reference S isn't moving, or we could say that both the ruler and the light saber are in the same frame of reference, what's important though is that the light saber measures a proper length Lo of Lo= Δx = x2 – x1. Proper length Lois very much like proper time Δto. Proper length is the length measured within an inertial frame of reference. In this case, x1 and x2 are simultaneous events since we made these measurements at the same time.
Frowning is appropriate. We said earlier that two events might be simultaneous in one frame of reference but not in another. What does that mean for distances?
That means that the length of an object will change depending on who's taking the measurement. More specifically, someone moving in a frame of reference S' with a relativistic velocity v will not measure the same length Loas we do. By how much will these two lengths differ?
Let's bring that frame of reference S' and make the same measurement of length but at time t'. What do we get now?
We defined length as Lo= x2 – x1. It seems only logical to define the length L' of a frame S' as L' = x2' – x1'. If we use our Lorentz-Einstein transformations, we can solve for x with x' = γ(x − vt) and get two equations, one each for x1 and x2, which are in no way as mischievous as Thing 1 and Thing 2.
Therefore, Lo= x2 – x1 = γ(x2' – x1') = γL', or
.
Someone whizzing past while simultaneously measuring the length of our light saber will find it smallerthan we do in our frame of reference. It's the opposite effect from the one on time.
After our discussion of time dilation, this phenomenon of length contraction doesn't seem so shocking, but it's still a little weird.
We mentioned length contraction when we gossiped and giggled about the Michelson-Morley experiment. Dutch physicist Hendrik Lorentz suggested the ether was actually contracting the apparatus by
.Although he was wrong about the reasons behind this relationship, his equation still holds. That's why length contraction is sometimes called a Lorentz contraction.
Math Break!
How much would a 100 m field seem to contract to a rocket passing Earth at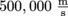
?
Good question. First, we find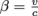
using 
, then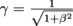 
.We find that β = 0.0167, and γ = 1.0084. That's mighty close to 0 and 1, respectively. Even a speed more than 100 times than our fastest Earth-made rockets barely registers the effects of relativity. Next, we calculate the length using Lo = 100 m, to find that L' = 99.16 m.
Once again, Shmoop comes to the rescue, well, Shmoop and the work of dozens of brilliant physicists. To the great relief of our order-loving minds, there is such a property. It's called a space-time interval.
What is a space-time interval?
We defined space-time coordinates as having a location and a time, which we can represent as s = (x, y, z, t) and use to describe an event like us waving at Gaspard from the train. Let's stick another event in there with space-time coordinates s' = (x', y', z', t'), maybe Gaspard frowning back. Since we're on the train, our y's and z's are 0. The difference in location between those two events would equal Δx = (x'− x).
We left out time so far. A space-time interval should be given by Δs = s'− s, to our thinking, and we're correct.
Space has units of length, like a mile or a meter. Time, on the other hand, has units of, well, time, like minutes or seconds. But space-time is a single entity, so it'd be nice if we could bridge length and time, which measure different things, without skewing our invariant quantity space-time.
Let's think about it, there is a measurement we use every day that relates distance to time…like miles to hours…How do we relate meters to seconds again?
Speed! Ding, ding, ding. You win.
And what's one speed that never changes, regardless of who measures it? Light speed.
Imagine a frame of reference S at rest with coordinates (x, y, z, t). Another frame of reference S' with coordinates (x', y', z', t') has a velocity v relative to S. Both frames intersect at their origins. At that precise moment, a light sparks at t = 0 and spreads out with a radius equal to ct, as seen below.
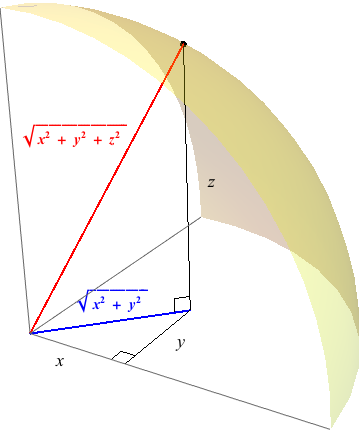
The speed of light multiplied by time gives us a unit of distance. In this case, it's simply the hypotenuse of the 3D right-angled triangle as you can see in the diagram.
Remember the two frames S and S' intersect at their origins. The frames end up with light spheres of ct and ct' respectively, which expand with time. As always, the speed of light c is constant in both S and S'.
We get, then, that s2 = x2 + y2 + z2 − (ct)2 and s2' = x'2 + y'2+ z'2 − (ct')2. If we take the difference between the two, we get that our space-time interval Δs2 = [(x'2 + y'2+ z'2 − (ct')2] – [x2 + y2+ z2 − (ct)2]. We can rewrite this as Δs2 = c2Δt2 − Δx2− Δy2− Δz2.
This is the one quantity that will never change between two frames of references. Space-time intervals are therefore invariant quantities.
That's nice and all, but what does it mean?
Our space-time intervals can take different values. They can be negative, positive or equal to zero.
If Δs2 > 0, we call this interval timelike. These two events have a causal connection; one precedes the other since there is a difference in time between the two. It also means the two events might have the same location, since the bracket with (-Δx2− Δy2− Δz2) could equal zero.
If Δs2 < 0, we call this interval spacelike. These two events do not have a causal connection; they could be simultaneous, since Δt could be zero, but cannot share the same location. Finally, if Δs2 = 0, we call this interval lightlike. These are dealing with events that travel at the speed of light, which only occurs for photons, light itself. We'll talk more about why objects with mass don't travel that fast soon.
Another trick to use is to remember the saying "moving clocks run slow". Time slows down for those moving at relativistic speeds. Length does the opposite: moving rulers contract.
Einstein worked in a patent office at the time he developed the theory of relativity. Constantly thinking about electromagnetic inventions might have contributed to the theory's development.
Everything in the universe is subject to electromagnetic forces. The only exception to this is gravity, which we'll chat about in just a bit. Light, as it turns out, also obeys the rules of electromagnetism. By the way, light also obeys the laws of gravity, but that's a topic left for general relativity, rather than the special relativity we're studying now.
It's time to apply some logic. The laws of electromagnetism can't change. That's why we call them "laws." Light obeys these laws, but (and this is a big but) the speed of light doesn't change by changing the frame of reference. Conclusion? The laws of physics don't depend on us, as the observers, or on our motion. In other words, there is no preferred frame of reference in which to do physics.
This exercise in logic is Einstein's first postulate for his theory of special relativity. It simply means that our frame of reference is not better than Gaspard's, Igor's, or the trashcan's for that matter.
It's a good thing Einstein wasn't around when Galileo got convicted. This first postulate pretty much insists Earth isn't special at all. The laws that formed our home planet are the same across the entire galaxy and beyond.
Einstein's second postulate is one we've already discussed. The speed of light is the same anytime, everywhere.
That's all there is to it, so why is it called Einstein's special theory of relativity? Most phenomena in the world can be described with electromagnetism, except for gravity. Gravity is a force causing acceleration, so the motion of objects under the influence of gravity can't be described with inertial frames.
Einstein's theory of relativity is special because it ignores acceleration. General relativity, on the hand, is generalized to include gravity.
Einstein didn't become a celebrity either in or out of the world of physics until his theory of relativity was verified experimentally in 1919. From then on, he became a household name.
The Relativistic Factor
Now, it's time to have some fun. Remember Galilean transformations? Did it strike anyone as bizarre that time was identified with t' = t along with the rest of the coordinates x, y, z? We'd always assume that time wouldn't change, regardless of a frame of reference. Uh, oh. We know what assuming does….Imagine the following scenario. To escape Gaspard's wrath, we jump into a spaceship with a mirrored floor (B) and a mirrored ceiling (A), as you can see in the diagram below. Our ship, called The Albertian,travels with speed v and has a length L. The floor of the ship has a "light clock" that emits a beam of light from the floor to the ceiling (tick) and bounces back to the floor (tock). So in this scenario, an event is defined as "tick tock." Therefore, the light beam travels a distance of d = 2L during one single event.
We also know that time is distance over speed—even our speedometers are labeled in miles per hour. The speed in the spaceship clock is the speed of light, c. According to ourselves, within our frame of reference S', the entire time Δt' the beam of light takes to travel up and down between the two mirrors (the event) is
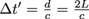.We're using all primes for our frame of reference S', and an observer can have everything without primes for reference S.Here comes an observer now. After we jumped into the spaceship, Gaspard pops up out of the bushes. To infuriate him even more, we bought the upscale model of The Albertian with windows so that he can see us out of his reach. Flabbergasted, he watches us zoom by at velocity v. We'll leave his enraged exclamations to imagination, where they belong. What does Gaspard see, apart from our triumphant grins as we wave him adieu?
A picture is worth a thousand words, especially Gaspard foaming with rage. Let's redraw the light clock from Gaspard's frame of reference S:
According to Gaspard, the light beam doesn't travel a distance d of 2L as it does in our own frame of reference. To him, the spaceship is moving, so the light bouncing between mirrors travels diagonally as the mirrors move with the spaceship as we can see in the diagram. To Gaspard,
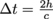.The distance the spaceship moves during the event according to Gaspard we'll call displacement x. The time from the spaceship to move from A to C is the same time as Gaspard's event time. . What's x? The Albertian is traveling at velocity v. Length or distance, as usual, is given by velocity multiplied by time, which in this reference S is x = vΔt.
And what's h? Yes, we need the hypotenuse of the right-angle triangle drawn above, with sides L and
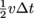, which is when we substitute in x = vΔt. Now, we're set to find h, crosssing our fingers that we remember geometry.Using Pythagoras' theorem, we know that
. We also know that 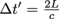, ,and x = vΔt. Therefore, , and .Substituting in the first equation of this paragraph, we get . Solving for Δt in terms of Δt' doesn't take too long. Besides, we're itching to know how to relate the time from one frame of reference to another.We define the fraction
as β (Beta), a ratio of a speed in terms of the speed of light. We can use it in to create 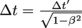Where there's one Greek letter, there's bound to be more. The quantity
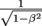appears so often in relativity that it's a lot easier to rename it the relativistic factor and assign it another symbol, γ (gamma), such that .The use of the relativisitic factor turns our derivation into Δt = γΔt'.
Ah, that's easier on the eye, and on the brain too. The time difference between one frame and another frame is calculable based solely on the speed between the two frames. That's because γ has the ratio of speed to the speed of light hiding inside β. Note that when β is near zero then γ = 1 and time is unchanged.
And that's how you can stop time.
Time Dilation
It's time to define another important term: proper time.Proper time is Δt' in the above equation and we often rewrite it as Δto (pronounced t-not, better understood as t-naught). Proper time is ourtime in this case, the time that we measure the light beam going "tick tock" while standing inside The Albertian. Think of proper time as the time in a frame of reference at rest, or the time according to something within the same frame of reference as the event.
Relativistic time, on the other hand, is the time Δt that Gaspard measures as he sees the light beam travel a diagonal path from A to C aboard our spaceship. If the light clock were down on Earth with him, he'd measure proper time and we'd measure relativistic time from aboard our space ship.
We can rewrite the equation we derived as Δt = γΔto. .
For the same event, we have two times: proper time and relativistic time. Time isn't a constant, like it seems to be for Gaspard and ourselves on the ground moving nowhere near the speed of light such that β = 0 and γ = 1 and all of Newtonian physics is true. On the other end of the speed spectrum, we know v can never be greater than c from Einstein's first postulate. This means that β < 1 and γ must always be larger than 1, so Δt > Δto, or the proper time is always the shortest measurable time.
For our now-familiar chase, Gaspard will measure the event (the tick-tock) as lasting longer than we will. One second for us is shorter than one second for Gaspard. In other words, time gets stretched out at relativistic speeds. This phenomenon is known as time dilation.
Let's say a particle zips through space at half the speed of light. By how much is its time dilated according to an observer on Earth? We'll be using Δt = γΔt'. We need to find γ first then, which depends in turn on
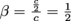. When 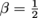, then 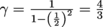.Earth time we'll call S, with particle time S'. Lastly we have 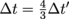. That's the dilated time according to earth. It's for the particle in terms of Earth time. Simultaneous Events
An event may be a special occasion such as a birthday. We were each born on a specific date, time, and location. Location + time = space-time coordinates, which are defined as s = (x, y, z, t). Anything with space-time coordinates is called an event.It shouldn't be that hard to decide whether or not two events occur at the same time, but only if we're within the same frame of reference. What if we raced Igor starting in the middle of the alley and we both ran in opposite directions with the same speed with two different finish lines the same distance from the starting point? Would we both cross the two finish lines at the same time according to everyone?
To answer this puzzling question, let's go back to your nocturnal escape aboard The Albertian. Unfortunately, our new state-of-the-art spaceship breaks down as we whiz past Gaspard in the darkness of the night. We're forced to improvise.
Our spaceship comes crashing back to earth at a merchandise train station. One of the wagon doors is wide open so we jump inside a cart of length L. There is nothing in the wagon but a small battery-operated lamp mounted on the center of the floor. Gaspard, having seen the spaceship crash, catches up just as the train takes off with a dashing relativistic velocity v. We want him to see our escape to rub it in so we flick on the light and proceed to smile and wave again.
What happens, according to you? Let's take a look at the drawing below:
As soon as we turn on the light positioned smack dab in the middle of the train car, two light beams shine from the center of the wagon and hit the two walls of the cart. Since light always travels at speed c, both light beams reach the two walls at exactly the same time. These two simultaneous events, according to ourselves, occur exactly 20 nanoseconds later than flicking on the light. If we assign our frame of reference the letter S', conveniently the same as before, then proper time Δto = 20 ns for a beam of light traveling at speed c to travel a distance equal to half the lengthof the wagon. We are using proper time Δto since we're in the same frame of reference as the light (event).
Now, let's look at what Gaspard sees as he shakes his fist at us.
Do both light beams reach the walls at the same time according to Gaspard?
The answer, as we've determined from the drawing, is no, or nein as our friend Einstein would say. Two events that were simultaneous in our frame of reference S' aren't simultaneous according to Gaspard's frame of reference S. It takes lessthan 20 ns for the left light beam to reach the wall, since the train is moving with velocity v so the back of the train moves towards the position from which the photon left the light fixtures, and morethan 20 ns for the right light beam to reach the other wall as that side of the train moves away from the position from which a different photon simultaneously left the light fixture.
In conclusion, two events that are simultaneous in one frame of reference aren't simultaneous in another if it's moving at a relativistic speed.
Lorentz-Einstein Transformations
Before we discuss the consequences of not-so-simultaneous events, let's revisit our Galilean transformations. Earlier we said that the coordinates of an event in one frame of reference S' moving with a relative velocity v with respect to another frame of reference S could be easily calculated asx' = x − vt
y' = y
z' = z
t' = t
These transformations assumed time was absolute as opposed to relative. We've also seen that time dilation occurs when speeds become a significant fraction of the speed of light. How do our Galilean transformations change when the relative velocity v of the two frames is relativistic, a significant fraction of the speed of light, c?
The derivation is left for you to do in Thoughts and Study questions. The resulting equations are called the Lorentz-Einstein transformations:
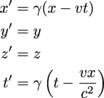
Remember that y and z don't change because v is exclusively in the x direction. We could easily rewrite these equations for objects moving in other directions, or define the x-direction as whatever direction the object in question travels. The x-coordinate is usually chosen because it eliminates height changes and varying an object's height would involve the force of gravity. This is chapter on special relativity, so gravity isn't welcome here.
From these, we may extract relativistic velocities ux and ux' in the same manner as we found Δt' in terms of Δt. We're spared the derivation—for now. The results are below.
At the risk, er certainty, of repeating ourselves, ux is the relativistic velocity of an object in frame of reference S, while ux' is the relativistic velocity in another frame of reference S'and v is the relativistic velocity between these two frames. There are some similarities to the time dilation equation we derived, but these velocity equations lack gamma.
The equations above are for finding the speed of one frame or the other. We can find the relative velocity between them by
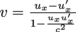.Length Contraction
Ready for some cooking? We get to mix time dilation with Galilean transformations and simultaneity.Oh, wait. We already did that, so now, let's turn our attention to length as measured in relativity. Since time changes in relativity, we had better expect the rest of space-time (the space part) to change, too.
A change in observed length is one of the consequences of multiple events occurring simultaneously in only one frame of reference.
One way of measuring the length of an object, say your (unopened) Jedi light saber, is to note both its ends on a ruler using the frame of reference S.
We could say that the frame of reference S isn't moving, or we could say that both the ruler and the light saber are in the same frame of reference, what's important though is that the light saber measures a proper length Lo of Lo= Δx = x2 – x1. Proper length Lois very much like proper time Δto. Proper length is the length measured within an inertial frame of reference. In this case, x1 and x2 are simultaneous events since we made these measurements at the same time.
Frowning is appropriate. We said earlier that two events might be simultaneous in one frame of reference but not in another. What does that mean for distances?
That means that the length of an object will change depending on who's taking the measurement. More specifically, someone moving in a frame of reference S' with a relativistic velocity v will not measure the same length Loas we do. By how much will these two lengths differ?
Let's bring that frame of reference S' and make the same measurement of length but at time t'. What do we get now?
We defined length as Lo= x2 – x1. It seems only logical to define the length L' of a frame S' as L' = x2' – x1'. If we use our Lorentz-Einstein transformations, we can solve for x with x' = γ(x − vt) and get two equations, one each for x1 and x2, which are in no way as mischievous as Thing 1 and Thing 2.
Therefore, Lo= x2 – x1 = γ(x2' – x1') = γL', or
.Someone whizzing past while simultaneously measuring the length of our light saber will find it smallerthan we do in our frame of reference. It's the opposite effect from the one on time.
After our discussion of time dilation, this phenomenon of length contraction doesn't seem so shocking, but it's still a little weird.
We mentioned length contraction when we gossiped and giggled about the Michelson-Morley experiment. Dutch physicist Hendrik Lorentz suggested the ether was actually contracting the apparatus by
.Although he was wrong about the reasons behind this relationship, his equation still holds. That's why length contraction is sometimes called a Lorentz contraction.Math Break!
How much would a 100 m field seem to contract to a rocket passing Earth at
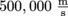?Good question. First, we find
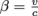using , then 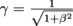.We find that β = 0.0167, and γ = 1.0084. That's mighty close to 0 and 1, respectively. Even a speed more than 100 times than our fastest Earth-made rockets barely registers the effects of relativity. Next, we calculate the length using Lo = 100 m, to find that L' = 99.16 m.Invariant Quantities
We've tossed time, length, velocity, and space coordinates all together into one big, gooey, melting pot. We've watched them all take on different, changing values that react to each other's changes. One changes, so does the other, and on and on. Location and time have no real meaning anymore. Our regular and ordered lives have become pure chaos. Is there even one specific property, or attribute, that never changes from one frame of reference to the next, regardless of velocity, effects of time dilation, length contraction, etc.?Once again, Shmoop comes to the rescue, well, Shmoop and the work of dozens of brilliant physicists. To the great relief of our order-loving minds, there is such a property. It's called a space-time interval.
What is a space-time interval?
We defined space-time coordinates as having a location and a time, which we can represent as s = (x, y, z, t) and use to describe an event like us waving at Gaspard from the train. Let's stick another event in there with space-time coordinates s' = (x', y', z', t'), maybe Gaspard frowning back. Since we're on the train, our y's and z's are 0. The difference in location between those two events would equal Δx = (x'− x).
We left out time so far. A space-time interval should be given by Δs = s'− s, to our thinking, and we're correct.
Space has units of length, like a mile or a meter. Time, on the other hand, has units of, well, time, like minutes or seconds. But space-time is a single entity, so it'd be nice if we could bridge length and time, which measure different things, without skewing our invariant quantity space-time.
Let's think about it, there is a measurement we use every day that relates distance to time…like miles to hours…How do we relate meters to seconds again?
Speed! Ding, ding, ding. You win.
And what's one speed that never changes, regardless of who measures it? Light speed.
Imagine a frame of reference S at rest with coordinates (x, y, z, t). Another frame of reference S' with coordinates (x', y', z', t') has a velocity v relative to S. Both frames intersect at their origins. At that precise moment, a light sparks at t = 0 and spreads out with a radius equal to ct, as seen below.
The speed of light multiplied by time gives us a unit of distance. In this case, it's simply the hypotenuse of the 3D right-angled triangle as you can see in the diagram.
Remember the two frames S and S' intersect at their origins. The frames end up with light spheres of ct and ct' respectively, which expand with time. As always, the speed of light c is constant in both S and S'.
We get, then, that s2 = x2 + y2 + z2 − (ct)2 and s2' = x'2 + y'2+ z'2 − (ct')2. If we take the difference between the two, we get that our space-time interval Δs2 = [(x'2 + y'2+ z'2 − (ct')2] – [x2 + y2+ z2 − (ct)2]. We can rewrite this as Δs2 = c2Δt2 − Δx2− Δy2− Δz2.
This is the one quantity that will never change between two frames of references. Space-time intervals are therefore invariant quantities.
That's nice and all, but what does it mean?
Our space-time intervals can take different values. They can be negative, positive or equal to zero.
If Δs2 > 0, we call this interval timelike. These two events have a causal connection; one precedes the other since there is a difference in time between the two. It also means the two events might have the same location, since the bracket with (-Δx2− Δy2− Δz2) could equal zero.
If Δs2 < 0, we call this interval spacelike. These two events do not have a causal connection; they could be simultaneous, since Δt could be zero, but cannot share the same location. Finally, if Δs2 = 0, we call this interval lightlike. These are dealing with events that travel at the speed of light, which only occurs for photons, light itself. We'll talk more about why objects with mass don't travel that fast soon.
Common Mistakes
It's oh-so-easy to confuse quantities which belong in S with S'. Pictures labeling all quantities involved in each frame of reference can help.Another trick to use is to remember the saying "moving clocks run slow". Time slows down for those moving at relativistic speeds. Length does the opposite: moving rulers contract.