ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Geometry and Measurement Videos 88 videos
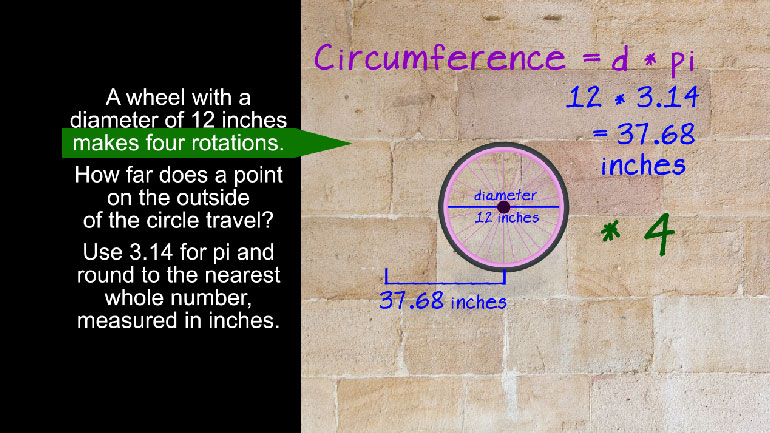
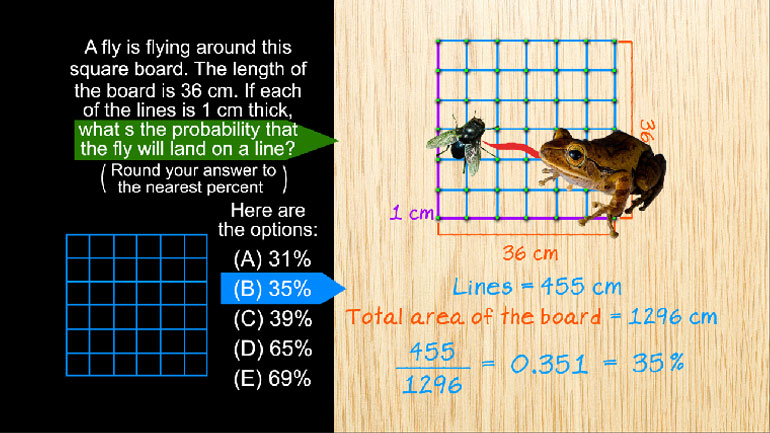
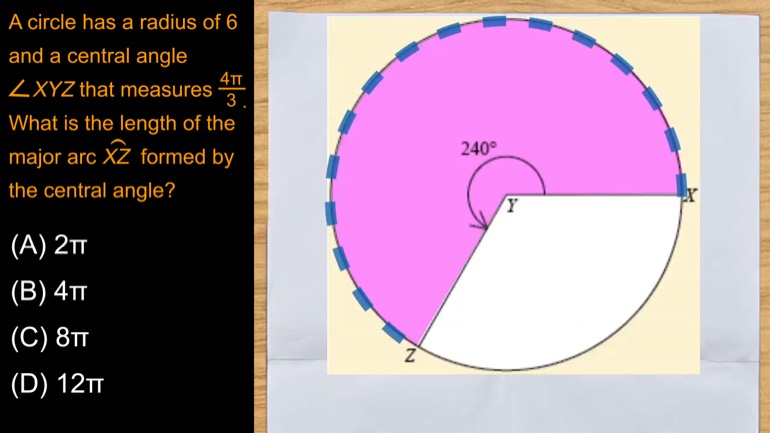
SAT Math 1.1 Geometry and Measurement. What is the circumference of the circle?
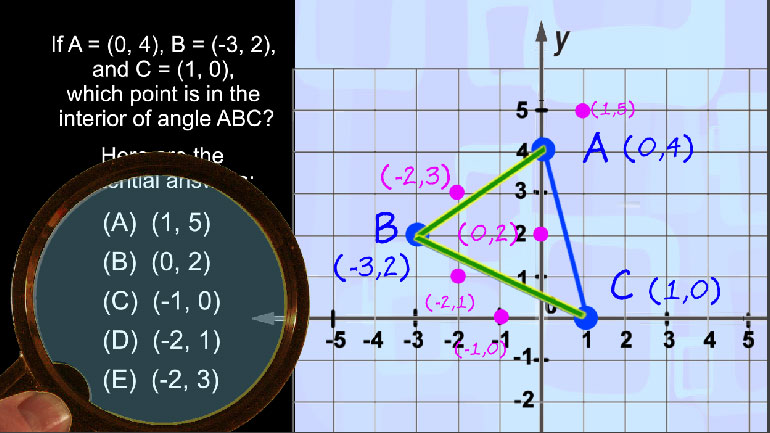
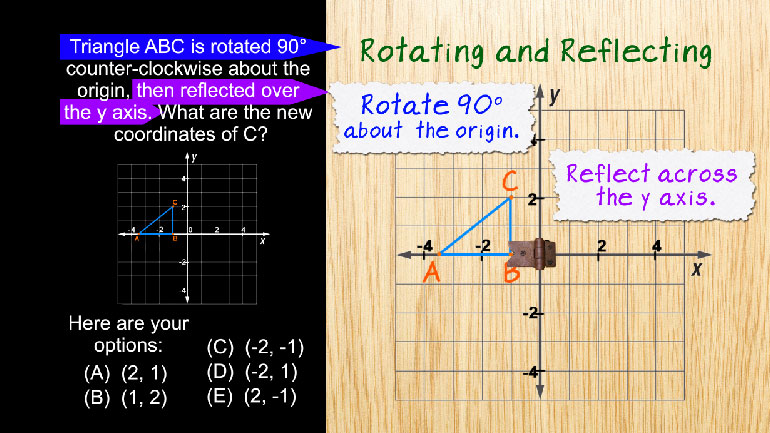
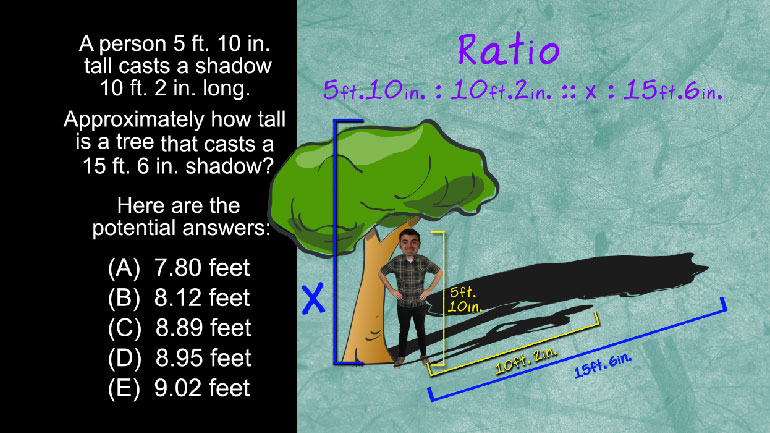
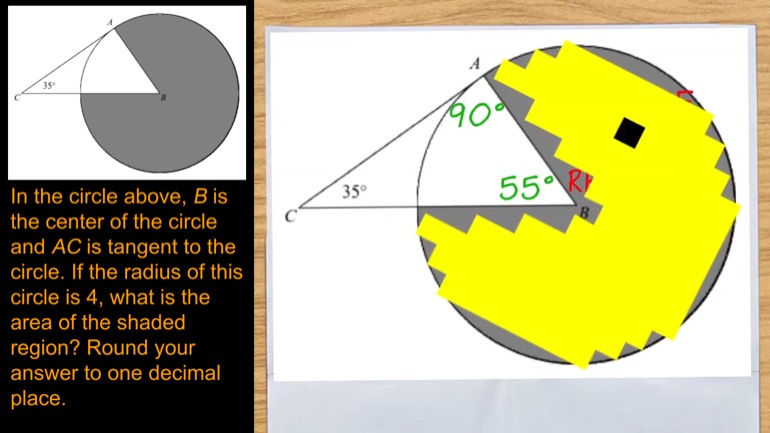
SAT Math: Geometry and Measurement Drill 1, Problem 2. If A = (0, 4), B = (-3, 2), and C = (1, 0), which point is in the interior of angle ABC?
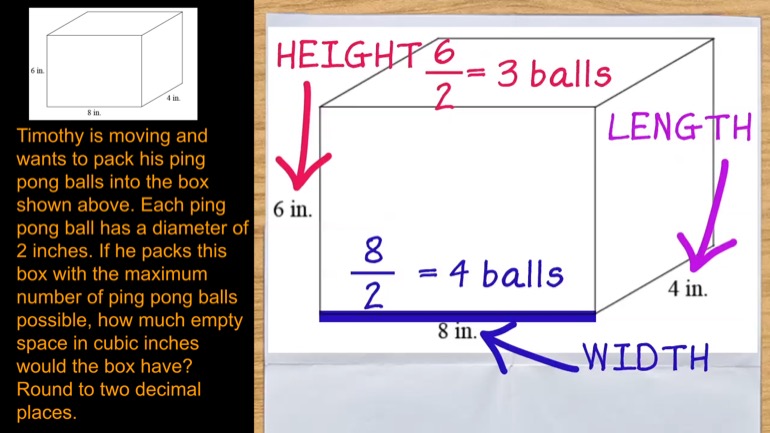
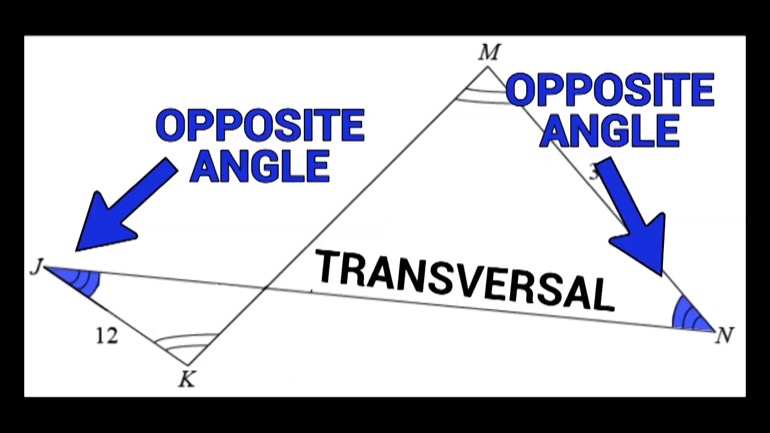
SAT Math 2.3 Geometry and Measurement. Find the length of AB.
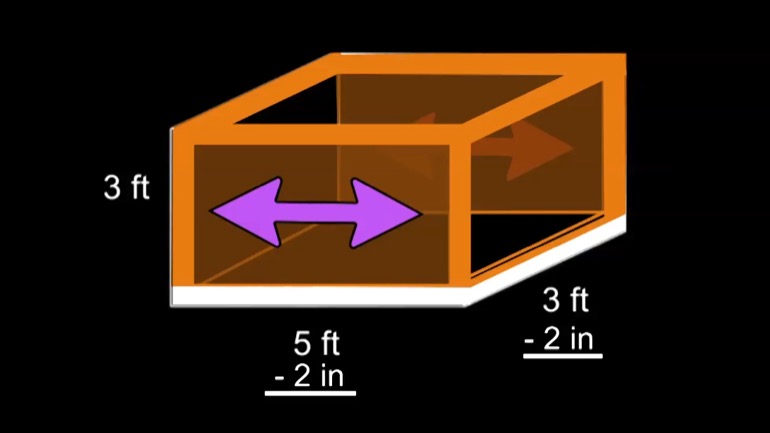
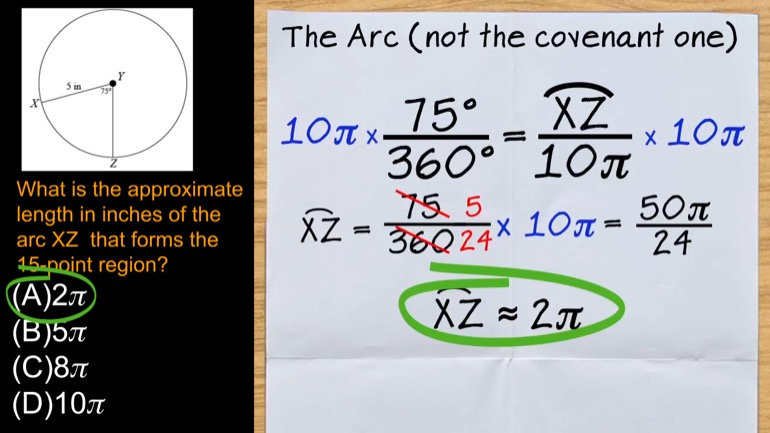
SAT Math: Working with Chord Lengths to Find the Radius of a Circle 3 Views
Share It!
Description:
In the circle above, the point A, which is in the middle of the chord, is 7 inches from the center of the circle. The length of the chord is 10 inches. What is the radius of the circle in inches? Round your answer to one decimal place.
Transcript
- 00:00
Yeah Whoa Okay Shh Trig shmoop er's Got a circle
- 00:06
in a line You gotta dot We got a letter
- 00:09
That's about it in circle above the point eh Which
- 00:11
is in the middle The cord is seven inches from
- 00:13
the center of the circle with length of the court
Full Transcript
- 00:16
is ten inches And that's ten inches from there to
- 00:18
there What's the radius of the circle in inches Run
- 00:22
your answer thereto One decimal place Okay so let's think
- 00:26
about this Well this type of cord has nothing to
- 00:29
do with the pleasant sounding music Like that's a chord
- 00:32
It's a line drawn on the edges of a circle
- 00:35
but it will help us find the length of the
- 00:38
radius How you ask Oh will answer for no extra
- 00:41
charge The problem says that a is seven inches from
- 00:44
the center of the circle Well that's rotate the circle
- 00:47
Teo make things a little easier It looks like that
- 00:50
Well the line from a to the centre is and
- 00:52
well perfectly vertical And that cord is perfectly horizontal so
- 00:57
they form a nice right triangle right there Well this
- 01:00
happens any time we create a line from the centre
- 01:02
to the midpoint of accord any cord right And we're
- 01:05
also going to note that it bisects the cord right
- 01:08
there So we got five on either side and now
- 01:11
we've got seven They're in a five They're in a
- 01:14
right triangle This is getting easier Well the radius is
- 01:17
actually the high Parton's of this right triangle And the
- 01:20
problem's states that the cord is ten inches long and
- 01:22
then point a's and centers We got five inches There
- 01:25
goes like seven inches So Noel let's use the Pythagorean
- 01:28
theorem It was his best serum the serum on how
- 01:32
to make a smoothie not so popular but this one
- 01:34
was good So we have five squared plus seven squared
- 01:37
equals R squared now twenty five plus forty nine or
- 01:40
seventy for is R squared So our is the square
- 01:42
root of seventy four It's about eight point six Well
- 01:44
the radius of the circle is about eight point six
- 01:47
inches Hearing that we've answered this cord problem frankly is 00:01:51.29 --> [endTime] music to our ears
Related Videos
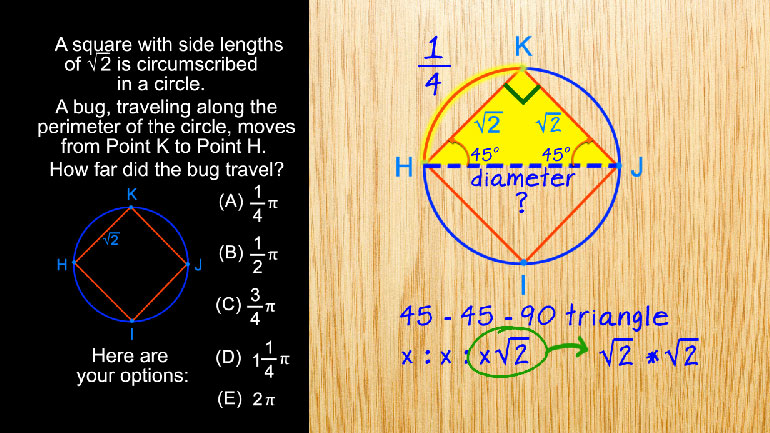
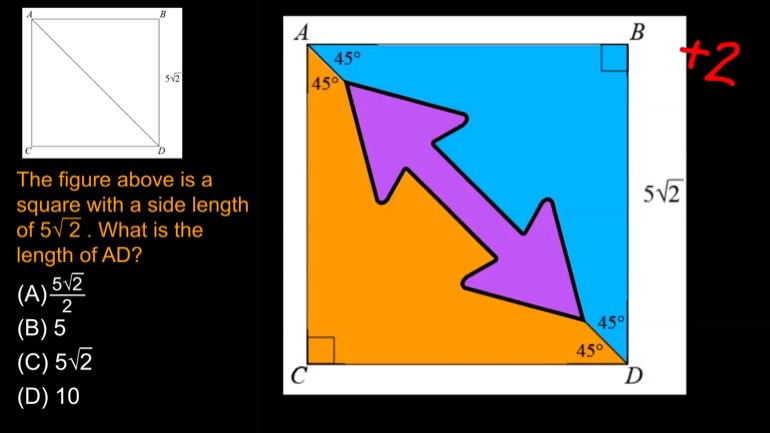
The figure above is a square with a side length of . What is the length of ?
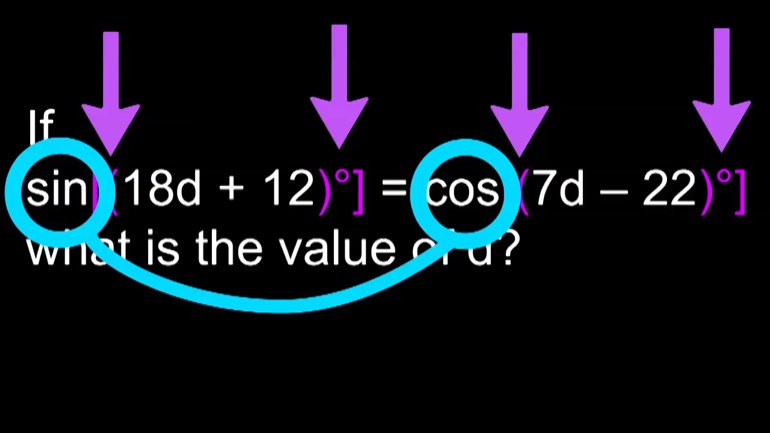
If sin[(18d + 12)°] = cos[(7d – 22)°], what is the value of d?
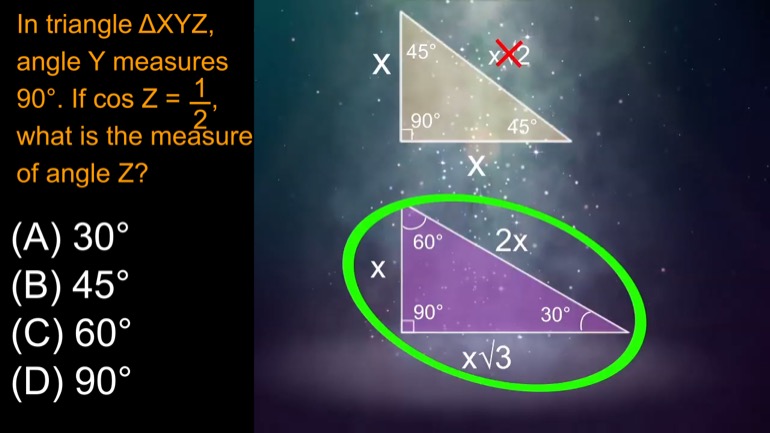
In triangle ΔXYZ, angle Y measures 90°. If , what is the measure of angle Z?
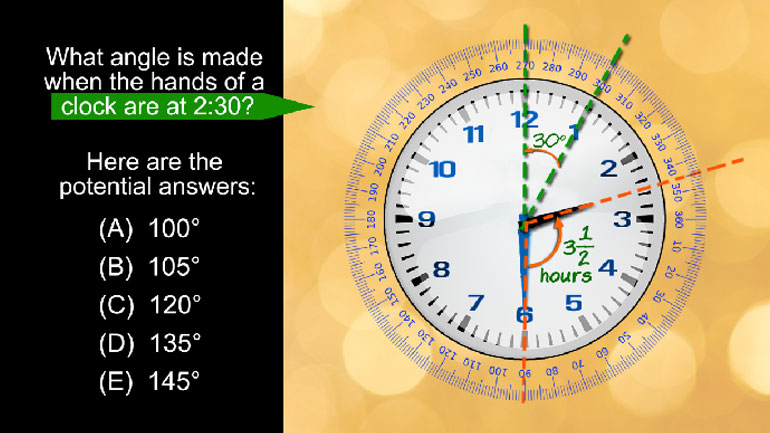
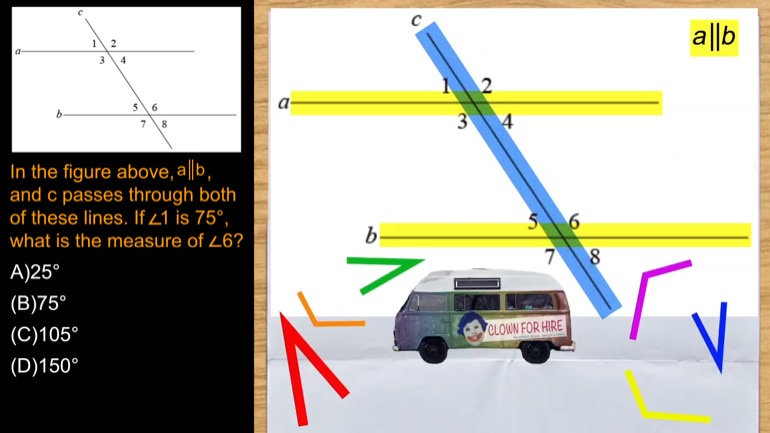
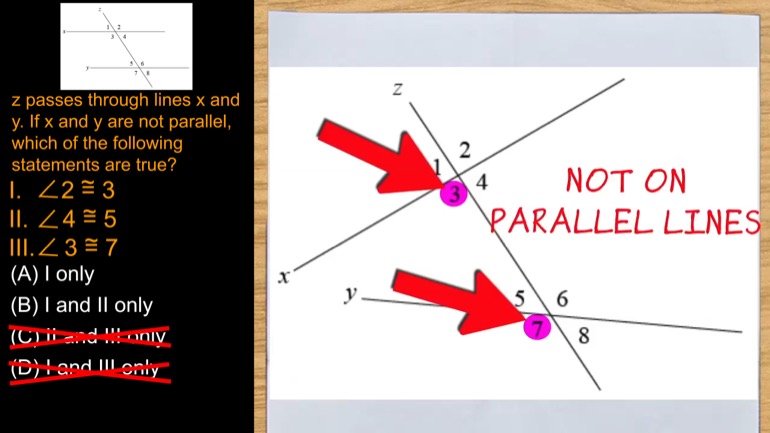
SAT Math 2.1 Geometry and Measurement. What is the measure of angle z in terms of x and y?