ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Tangents and Secants Videos 5 videos
Ever had someone tell you that getting pooped on by a bird was good luck? Yeah, we never fell for that one either. Watch this video to see how math...
Secant Angles 841 Views
Share It!
Description:
Don't try this at home, Shmoopers.
Transcript
- 00:04
Secant angles, a la Shmoop.
- 00:08
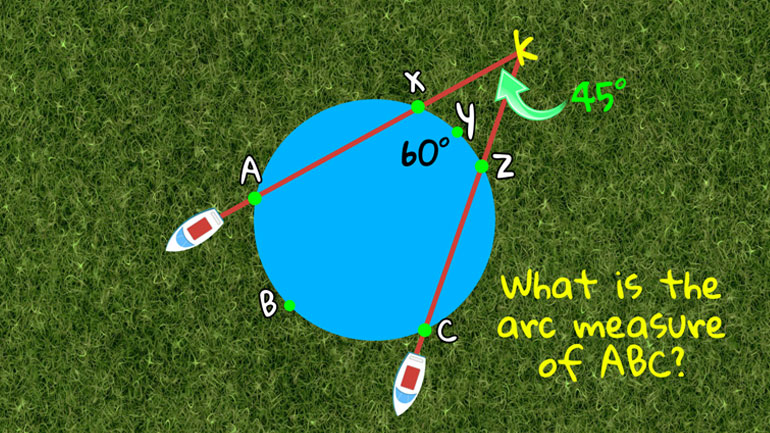
Roger Goosebuss has invented a new amphibious vehicle that he would like
- 00:12
to test for navigational accuracy.
- 00:15
To do this, he employed two of his new vehicle prototypes and a perfectly circular lake…
- 00:19
…located a few miles from his manufacturing headquarters.
Full Transcript
- 00:23
To test whether his vehicles are capable of traveling in exactly straight paths…
- 00:27
…Roger will have the vehicles take off on two routes that form an angle of 45 degrees.
- 00:33
They will reach the lake at two points, forming an arc of 60 degrees…
- 00:37
…and then they’ll continue their respective paths across the lake,
- 00:40
arriving somewhere on the opposite shore.
- 00:42
If their journey is successful and the vehicles travel in perfectly straight lines…
- 00:47
…what should be the arc measure between them when they arrive on the far shore of the lake?
- 00:55
The formula for finding any arc or angle measure involved in a secant angle problem such as this…
- 01:01
...is secant angle K equals one-half the difference between the measurements of the
- 01:06
far arc A-B-C and near arc X-Y-Z.
- 01:10
With this formula, it’s a simple matter of… plugging in.
- 01:13
The secant angle of 45 degrees equals 1/2 the difference between the measurement of
- 01:17
the far arc – that’s our unknown…
- 01:20
…and the near arc measurement of 60 degrees here.
- 01:23
Multiply both sides of the equation by 2 to cancel out the 1/2 on the right side.
- 01:27
45 times 2 equals 90, so you get 90 degrees on the left side...
- 01:31
equals arc A-B-C minus 60 degrees.
- 01:34
Add 60 degrees to both sides of the equation and we have the solution:
- 01:38
Arc A-B-C should be 150 degrees… if the experiment goes as intended.
- 01:44
Now that all of the theoretical measurements are in order, Roger’s ready to begin the test.
- 01:48
Perhaps he should have factored in a few more variables… like… actual geese, for example.
- 01:53
This has turned into a real honk-fest.
Related Videos
This video can run circles around other videos about circles. Sir Cumference, of Round Table fame, explains all the properties of… well, circles....
Time to learn about the area of a sector. And no, that's not the sector's bedroom with a bumper sticker on the door that reads, "GO AWAY."
Equations of circles are a no-brainer. If aliens can do it, so can you. All you do is substitute the center of the circle's coordinates into the eq...
It's super useful to be able to find the distance around stuff. Like when you’re being pursued by authorities while running around the base of an...
ACT Math: Plane Geometry Drill 5, Problem 4. What is the radius and coordinate center of the circle?