Balance is important to everyone. It keeps you from falling over when you want to

• walk without tripping over your own feet.
• pop a wheelie—whether on a bike or in a wheelchair.
• show off your slackline skills to those cool college students in the park.

Even those of us a little more gravity-challenged still manage to maintain balance most of the time. Some people even make careers out of being good balancers, like gymnasts, figure-skaters, ballerinas, and those people who can ride unicycles while juggling chainsaws.

(How does someone even realize they have a talent for juggling chainsaws? Do circuses send out talent scouts to lumber mills or something?)

Balancing binary trees isn’t quite as exciting as all that, but it also doesn’t involve defying death. That’s got to count for something. Even if you aren't making the big bucks for your balancing skills, if you can't balance at all, you can't get things done. Just like with balancing in real life, balancing binary trees helps keep things running at peak efficiency.

Think about it this way. If you lost your favorite Hello Kitty beanie somewhere in an unfamiliar room in a creepy old (probably haunted) mansion, you’d want to find it. Fast. You and your best friend divide the room in half to search it. That’s all well and fine until you open a door on your half that leads into another room with more doors that lead to more rooms.

Don't mind the fact that it’s unlikely you’ll find your beanie in rooms you’re only now discovering. The house is haunted, remember? Who knows where Casper or Peeves left your precious cat hat.

Now that you know about all those countless other rooms on your half of the room, the search is now lopsided because your half is way bigger than your friend's. Your friend's going to finish way before you and probably go take a nap or something while you have to search all those extra rooms all by yourself.

That’s not very efficient.

It isn't efficient in computer science, either. A balanced tree in computer science doesn't need to be perfect (it doesn't need every level to be full) for it to be balanced, but every height level except the last one to be completely filled. That means it can’t look like this:

 

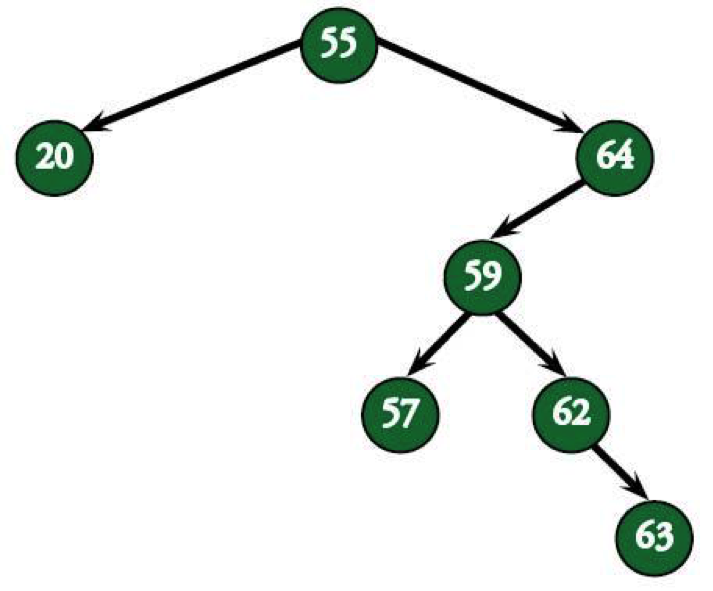
Yeah, this guy would clearly fall over in the real world. Just look at it. It’s like a chinchilla trying to play seesaw with manatee. Good luck with that one, little guy.

First off, node 64’s left subtree has two more levels than its right subtree. To make matters worse, 55’s right subtree is has 3 more levels than its left subtree. Not only that, but a tree with 7 nodes should, theoretically, only have a height of 2 (since 2^{2 + 1} – 1 = 7). This monstrosity actually has a height of 4.

That's much less efficient.

It should only take 2 tries to find a node in a 7-node tree, but you might need 4 tries to find 83 in this one. Just think about all that time you could have saved—time you could have used to practice chainsaw juggling—if only this tree had been balanced.

That’s really the main problem with unbalanced trees: they want to waste your valuable time (and processing power if you happen to be a computer).

Let's look at another example, playing the game, "Is it Balanced?"

 

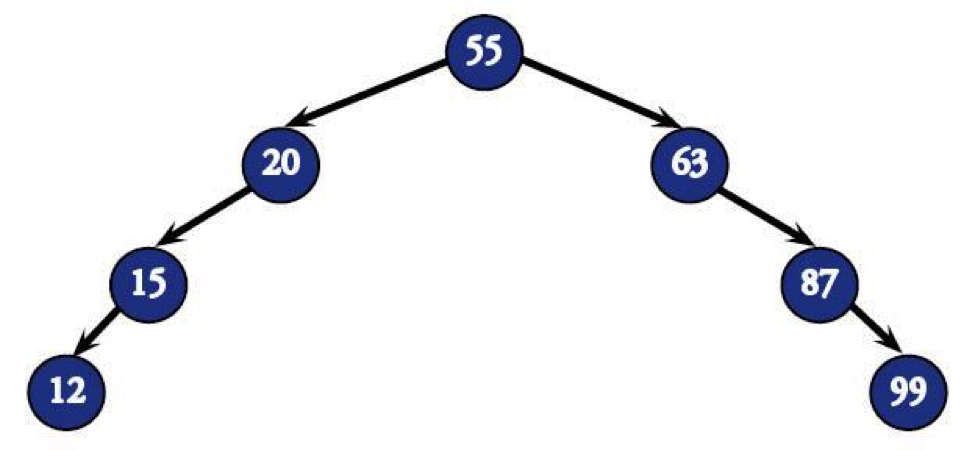
Here's where real life and computer science diverge a teensy bit. If you made a real-life model of this tree, it would balance like a pair of opened pliers. This tree is just being sneaky, though. If you take a closer look, the right subtree of 20 and the left subtree of 63 both have heights of 0, while the subtrees opposite them have two more levels. This unbalanced BST wants to waste just as much of your time as the last tree did.

Don't waste your time with unbalanced trees. Instead, spend a little time making it…balanced.

To make things more balanced, you'll want to follow an algorithm like this, starting from the root:

1. Look at the node's children. 
2. If the left subtree is has more levels than the right, assign the current node a code with two numbers. The first number should be the number of levels more that the left subtree has than the right, and the right node should be 0. If the left has one more level, the code is 10. If it has two more levels, the code should be 20.
3. If the right subtree has more levels, the code is the opposite: the left side gets a zero and the right gets the difference. If the right has one more level, the code should be 01, and if it has two more levels, the code should be 02. 
4. If the two have an equal height, use the code 00.

With these options, it becomes pretty clear where the rebalancing needs to be done.

For example, after the algorithm is run on the last tree, you can see that the tree is most unbalanced in nodes 20 and 63, but becomes balanced again once you get to 55. If you were to rebalance this tree yourself, you'd probably want to start around 20 and 63 because…they're in the worst shape.

 

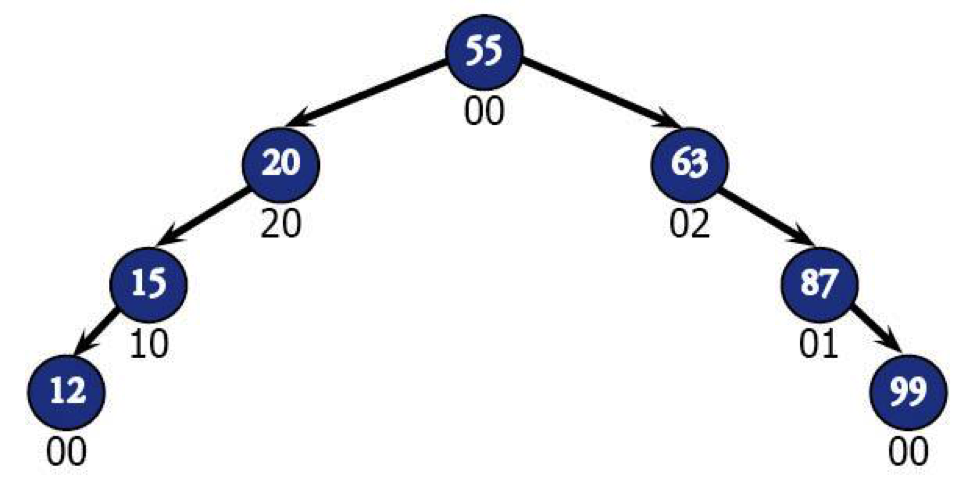
If this tree happened to be self-balancing though, it would never have gotten to look so unbalanced in the first place. It would look more like this:

 

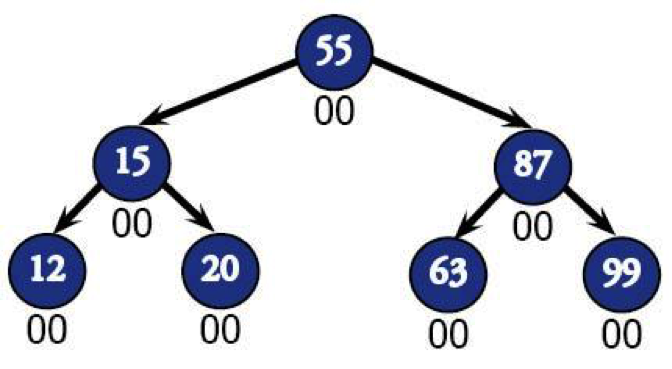
Yep, self-balancing binary trees are a thing, and they can save you ridiculous amounts of time manually balancing your trees. That way, you can get back to your unicycle chainsaw juggling practice.

You may lose a couple fingers along the way, but it'll all be worth it when you can effortlessly toss dangerous electric machinery while people wonder why anyone would want to practice that.