The trees we create need to fight the good fight against becoming

• lopsided.
• unbalanced.
• inefficient.
• improperly filled.

We want to make sure they live up to their fullest potential, (even if their lowest level isn’t completely filled) by using balance, efficiency, and binary. That’s how.

Balance

Let’s start with balance. We have to know for sure that a self-balancing tree will always balance itself after inserting a node. There's also the issue of how, after all nodes have been inserted, we know the tree's balanced.

The answer isn’t exactly epic, but it’s powerful: repetition. When a tree inserts a node, it has to double-check itself and correct itself if there’s an issue. If that happens at every single insertion, there’s no way that a tree will stay unbalanced. Since there are balance checks at every level and node of the tree, the tree can pinpoint exactly what subtrees/nodes need to be rebalanced, leaving the other nodes alone.

Here’s a fun hypothetical to keep you up at night: could a tree go through a rebalancing process and end up as unbalanced as (or more unbalanced than) it was before, and could it swap nodes that didn’t need to be swapped along the way?

Ignoring any conspiracy theories, there's no way this'll happen. Not even if pigs flew, cows jumped over moons, and Pluto became a planet again.

(Poor Pluto.)

Say we have a tree like this:

 

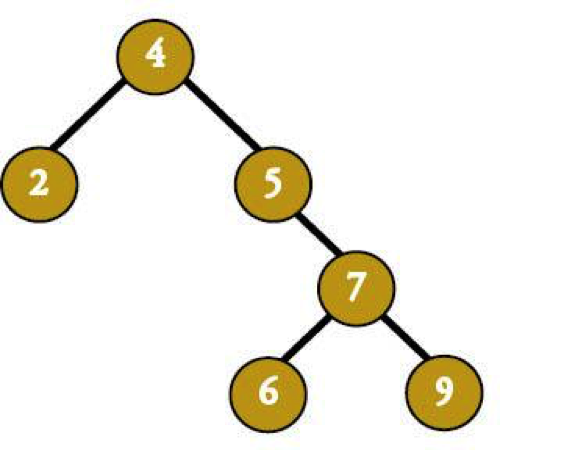
Say we'd just inserted 6. The balancing algorithm would change the tree to make the 6 more balanced.

 

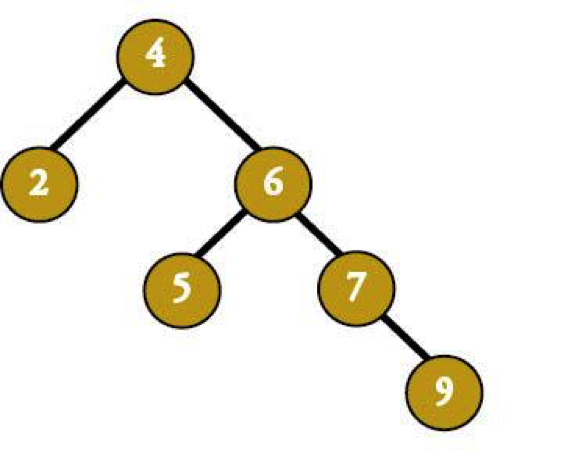
That's…less than balanced.

The good news? This tree would never happen, even before node 6. Any self-respecting (and self-balancing) tree wouldn’t get into that mess in the first place. It would've looked like this by the time we needed to insert 6 (assuming our node-insert order was 4, 2, 5, 7, 9):

 

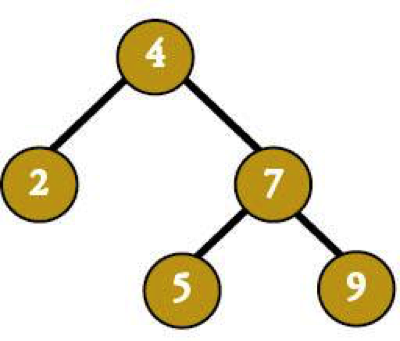
Just like that kid in your class with the on-point liquid eyeliner, trees work hard to keep themselves looking good. If they start out self-balancing, you'll never end up with and unbalanced tree.

Efficiency

We know, we know, we've been raving about the Binary Search Tree's efficiency since the beginning, but where's the proof? The proof, usually found in the pudding, is actually in the structure this time. When you put all lesser nodes to the left and all greater ones to the right, if you compare the parent node, you can completely eliminate one half of the tree with just that one comparison. Cutting the search space in half at every comparison cuts a lot of time fast.

It's that simple.

Binary Structure

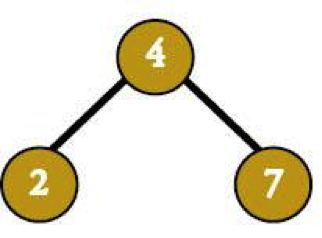
The binary structure is also useful in making sure that there's always a place for a new node, whether it’s less than or greater than any of the nodes currently in the tree (no such thing as equal-to nodes here). In a pinch, a tree can always create a new layer of leaves (and then rebalance, of course), like when inserting 5 into this tree as a child of 7.

 

Theoretically, we could get even better performance if we used a higher base, like 4, 7, or 10. Then, instead of cutting the list of choices in half every time, we could cut it by three quarters, six sevenths, or nine tenths. Theoretically, we could use a bed sheet as a parachute and jump off our roof.

Theories don’t always work in real life.

First of all, the biggest performance gain happens between unary and binary trees, so binary trees are proportionally more efficient. For example, if we were to create a unary tree for every person on the planet, it would have a height 7.5 billion or so with one node per level of the tree.

Zoinks!

This tree would be horribly inefficient. Compare that to a base-two tree with the name number of nodes, but a height of only 33. That’s much easier to find things.

We could also try a ridiculously wide tree only 2 levels high, with a base of 7.5 billion. The efficiency we’d gain using this tree instead of a base 2 tree (height 2 versus height 33) isn't really that impressive since we'd have to look at a bunch of nodes at each level—even if there are only two. Not compared to the rise in efficiency when going from 7.5 billion to 33. Binary trees give you the most bang (erm, efficiency) for the smallest buck (read: increase in base).

But say that didn't matter and we didn't care about the proportions of gains from one to the other. Binary trees give you an easy way to evaluate how to move through the tree: the value you're looking for is either greater than, less than, or exactly the one you're looking for. Try doing something similar for 4, 7, 10, or 7.5 billion branches per node. We dare you.

Even a 4-year-old can quickly figure out whether one number is bigger or smaller than another, which makes binary trees very easy to program.

Also: computers are literally built on binary. Logic gates are either open or closed. It just makes sense to use binary notation as much as possible when you're working with them. You could totally create a base 4, 8, or 16 tree from a binary tree but who has that kind of time? How would you decide upon 4, 8, or 16 ways to split your data? You’re looking at a massive programming headache.

A self-balancing, binary structure makes trees much easier to add to, delete from, and search. Nothing disrupts their Zen sense of perfect balance.