If you’re the observant type, you’ve probably noticed that every binary tree in this learning guide has been organized so the left child of any node (whether a root or one of those random nodes in the middle) is less than that node either by number or alphabetical order. That isn't always how it's done with trees, but it is the classic organization for a little something we like to call a Binary Search Tree.

If you noticed this pattern, great. If not (or if you just don’t believe us) go back and check. We double-dog dare you.

(Everyone knows that's five times as powerful as a normal dare.)

Binary Search Trees (BSTs) are crazy good for searching. If you’ve got a list of the nodes in the tree, you can pinpoint exactly where each one should be based on the tree’s structure. If it isn't there, you'll only need to check the number of nodes equal to the height of the tree to figure that out.

If you have a complete tree, that's fast.

For example, say you’re searching for node 6 in the following tree.

 

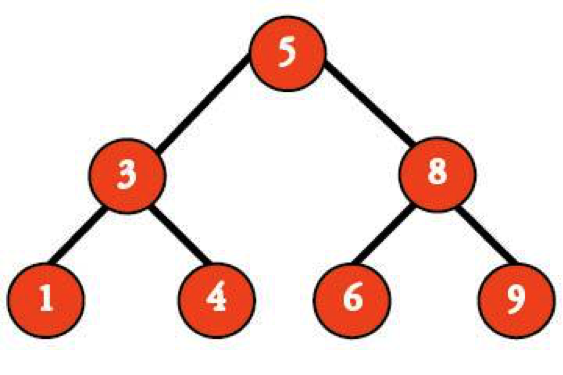
First, we see that the root is 5. If we look at 5 and notice that it is, in fact, less than 6, we can head straight to the right, since everything on the left is less than 5 (and therefore less than 6). So…we'll head right.

 

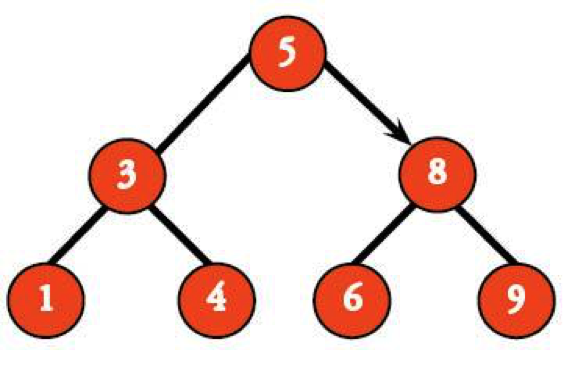
That brings us to 8. Just like 5, 6 is less than 8, so if it's in the tree, it must be in the left subtree of 8. And…it is.

 

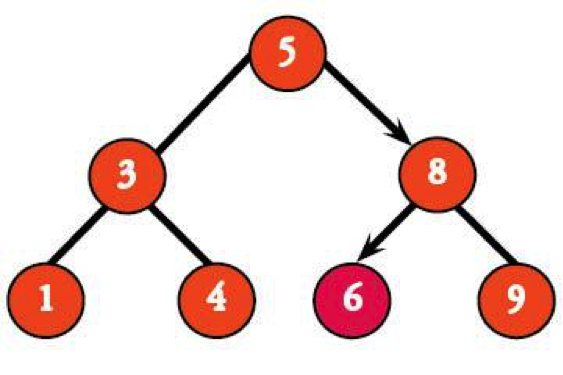
Maybe you think we’re making a big deal over nothing. You might say that now, but just wait till you have a massive tree in a program and need to find a bunch of values in it. Let's talk about a bigger example.

Say you've got a tree with 15 nodes and a root at 55. You think there's a node with the value 37, but you aren't completely, 100% sure. That means you'll need to dive into the tree and look for it. Lucky for you, it’s a BST. The easiest way to find your node is to compare values from root downward. That way, each evaluation can cut out up to half of the values.

 

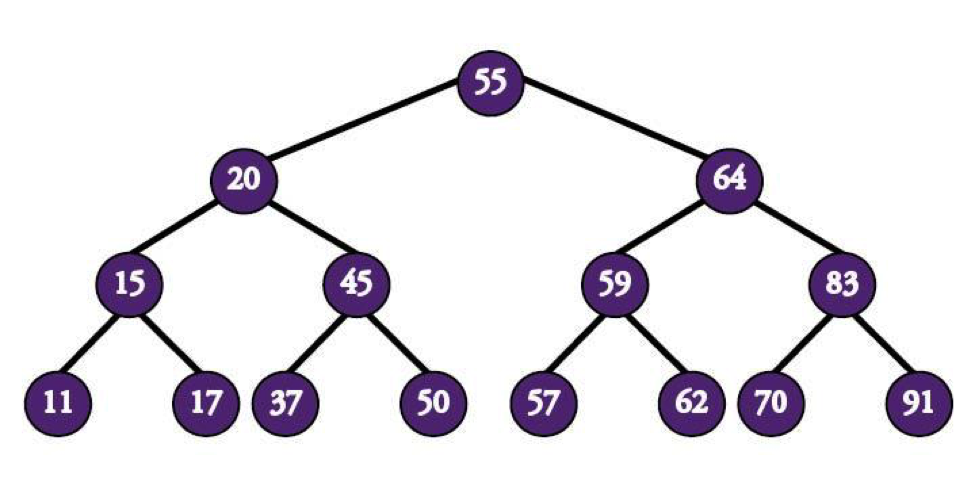
Since 37 is less than 55 (last we checked), you first veer left.

 

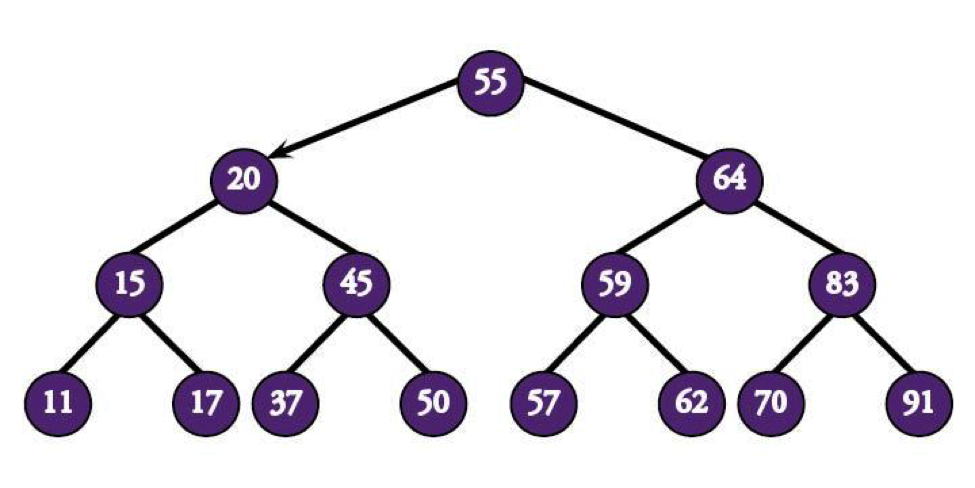
Then right, since 37's greater than 20.

 

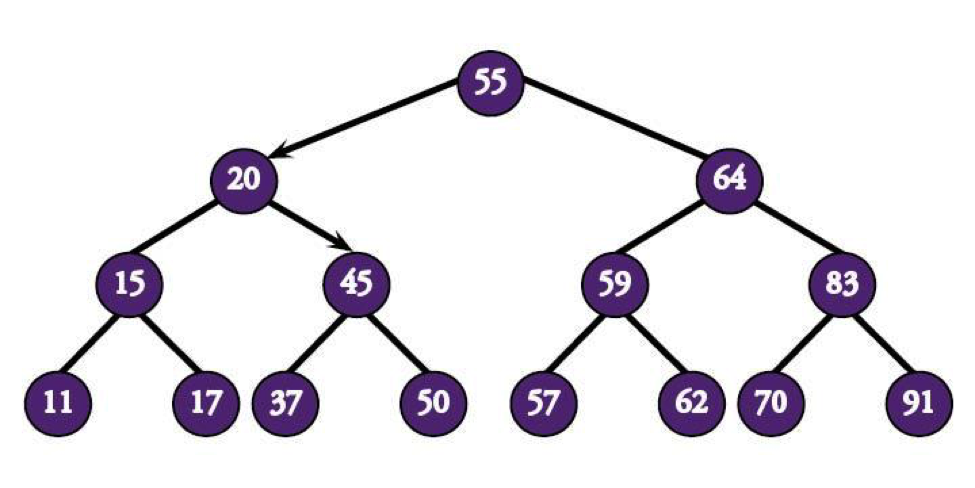
In a shocking turn of events, 45's greater than 37, meaning you head left and find the node in only four comparisons. Not bad.

 

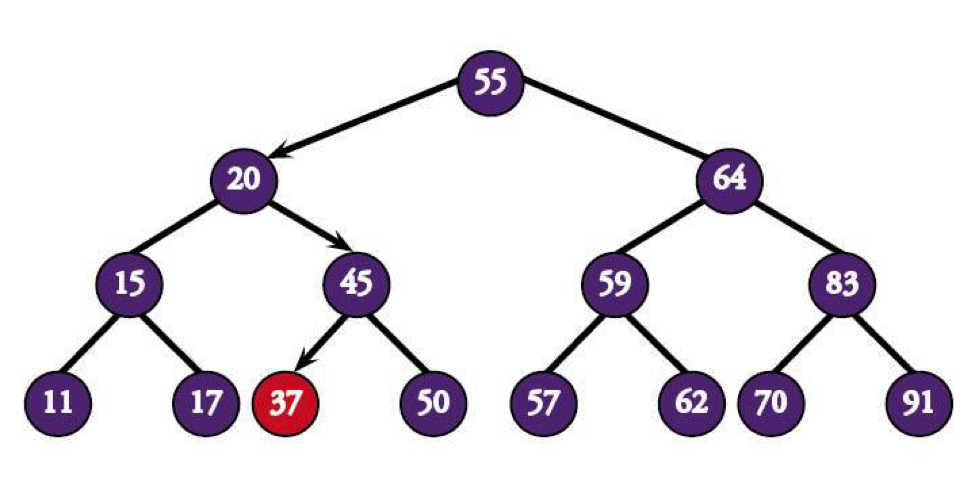
This might look like a set-up, but you could find any node in the tree in only 4 comparisons or less. Even with a small tree like this one, a maximum of three tries to find the right node is much quicker than trying to guess the correct one from the entire list of 15 (which could take 15 comparisons to find).

If you want the math behind that, a perfect BST tree with 2ⁿ - 1 nodes will you take at most n tries to find the right one. 2⁴ - 1 is 15, which means the maximum number of questions you need to ask the tree is 4.

We’re dealing with powers of two here, which means that the number of nodes need to double before you'll add another value to n. Not such a big deal with five, ten, or 25 nodes, but if you've got hundreds or thousands of nodes? That's huge. And it's all logarithmic.

If every node branches twice, you're actually dealing with a height that's logarithmic (base 2) to the number of nodes. If the height can only be log₂(n), then you'll only need n + 1 comparisons to find any node in the tree. Even a perfect tree with 1023 nodes (2¹⁰ - 1) will take a maximum of 10 comparisons to find any given node, since log₂(1023) rounds up to 9.

The simplest tree that still has any nodes has only one node: the root. The number of nodes in the tree is therefore actually 2¹ - 1. Since the root of the tree is left out of its height, this tree has a height of 0, or 1 – 1. This height can be found by taking the log₂(n + 1) - 1. If the tree isn’t full (if all its levels don't have the maximum number of nodes), you'll need to round log₂(n + 1) up before subtracting 1.

All thanks to the BST. You're welcome.