Say you have a pet wolverine. Why? Maybe you go to the University of Michigan—or maybe you want to someday—and really wanted to get into the spirit by owning your own mascot.

That's kind-of clingy, TBH, but still pretty cool because…wolverines.

There are many reasons we don’t recommend wolverines as pets (no offense, UMich). The worst of all—worse than all the frayed couch legs and shredded clogs—is that they're nearly impossible to potty train...we hear. That said, let’s say your pet wolverine, Frances, gets loose one day. Now you have to go look for him.

Your house is in the middle of your street. To search for good old Frankie, you could search your house first and then work your way left from your house down the street and then back right, but that’s just like the pre-order search. We've been there, done that, bought a Go Blue t-shirt.

Instead, you're going to try the in-order traversal to see how it would work.

You’re going to go out your door, turn left, and go all the way to the end of the street before you start searching, mostly because that last house has a badger Frankie-boy likes to visit (probably to watch Big Ten football games together). In any case, you’ll start there and work your way in order from one end of the street to the other. That means you’ll visit your house in the exact middle of your search. That's great because you’ll probably want a snack by then.

That’s pretty much how an in-order n-ary tree traversal works, but just in case wolverines and snacks distracted you from the whole point of that ridiculous totally believable story, let’s look at some pseudocode to clear things up a bit—with some comments to explain it on the right.

FUNCTION in_order(node):	/*function in_order*/
	in_order(left_node)	/*run in_order on the node*/ 
				/*to the node’s left*/
	IF node:		/*visit the node (as long */ 
				/*as one is there to visit)*/
		visit(node)
	ELSE:			/*if there is no node present*/
		return		/*pull out of the recursion*/ 
				/*by one level*/
	END IF
	in_order(right_node)	/*run in_order on the node*/
				/*to the node’s right*/
END FUNCTION

If you were following along from the pre-order traversals, you'll notice that the calls look about the same but the ordering changed slightly. If we're talking about the tree of trees, while Gnarltree is still the starting node, it won’t actually be the first node the algorithm visits.

 

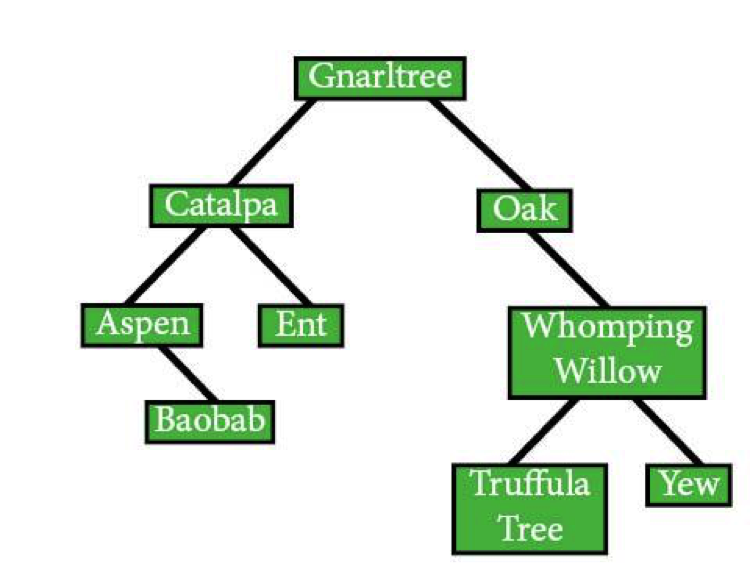
Actually, this algorithm makes a point of not visiting any node until it hits the leftmost leaf. That means it'll go from Gnarltree to Catalpa to Aspen without visiting a single node. You can wave if you want to, but no stopping.

in_order(Gnarltree)
	IF in_order(Catalpa)
		IF in_order(Aspen)

Only when it reaches Aspen (and can't keep running left) does it actually visit any nodes.

in_order(Aspen)
	IF in_order(NULL)	/*try to run in-order on Aspen’s*/ 
				/*left node*/
		ELSE		/*but there’s nothing there*/
			RETURN
	IF Aspen:
		visit(Aspen)

 

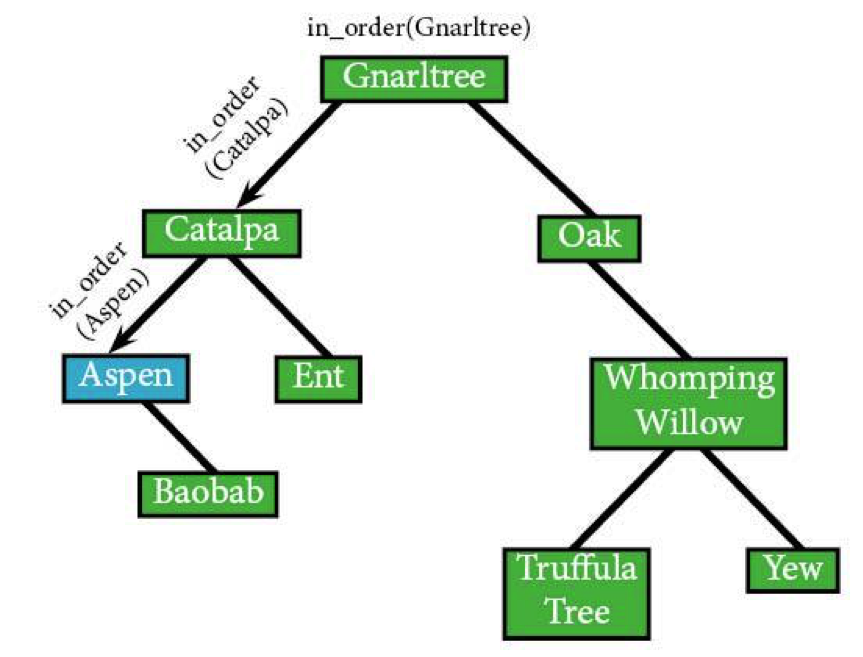
It came, it saw, it Aspened, so it's time for the algorithm to visit Aspen’s right node, Baobab. Since Baobab has no left children, it'll visit Baobab next.

in_order(Baobab)
	IF in_order(NULL): /*try to run in-order on Baobab’s*/
		ELSE	   /*left node, but there’s nothing there*/
			RETURN
	IF Baobab:
		visit(Baobab)

 

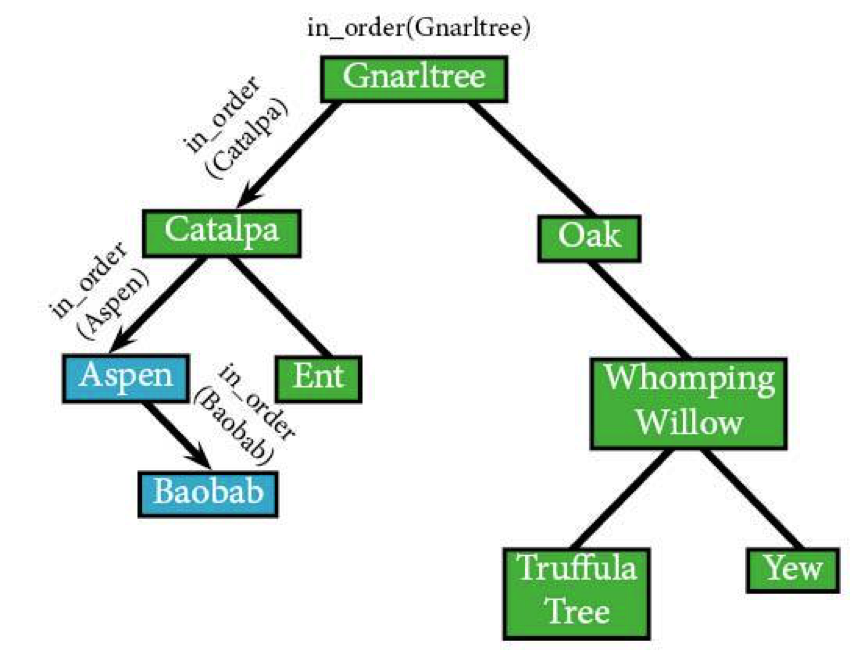
Baobab doesn't have any right children either, so the algorithm's going to return up to in_order(Aspen).

 

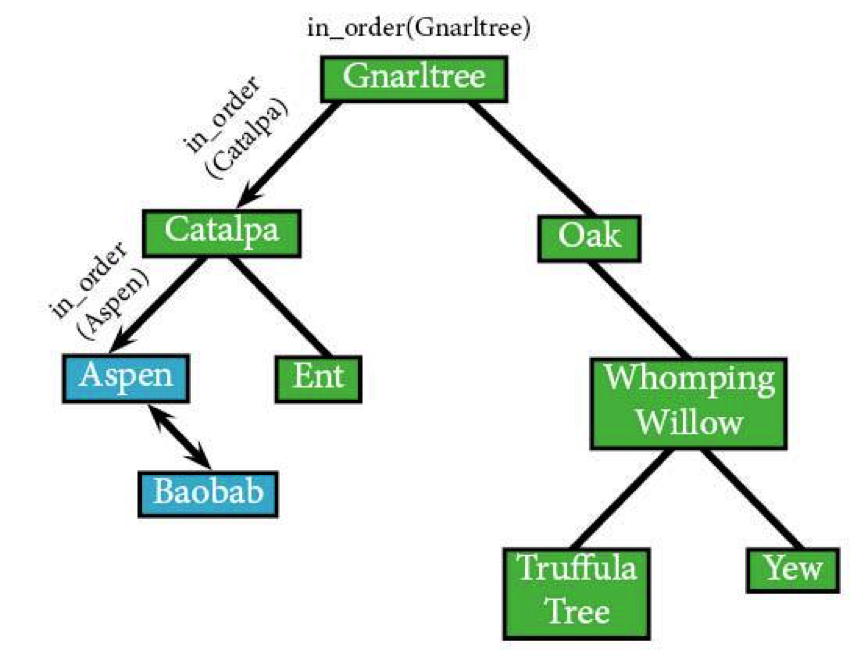
The algorithm has visited all of Aspen's subtrees. We know that because it finished looking at both the left subtree (even though it doesn't technically exist) and the right. That means the algorithm's going to hop one more level up to in_order(Catalpa).

 

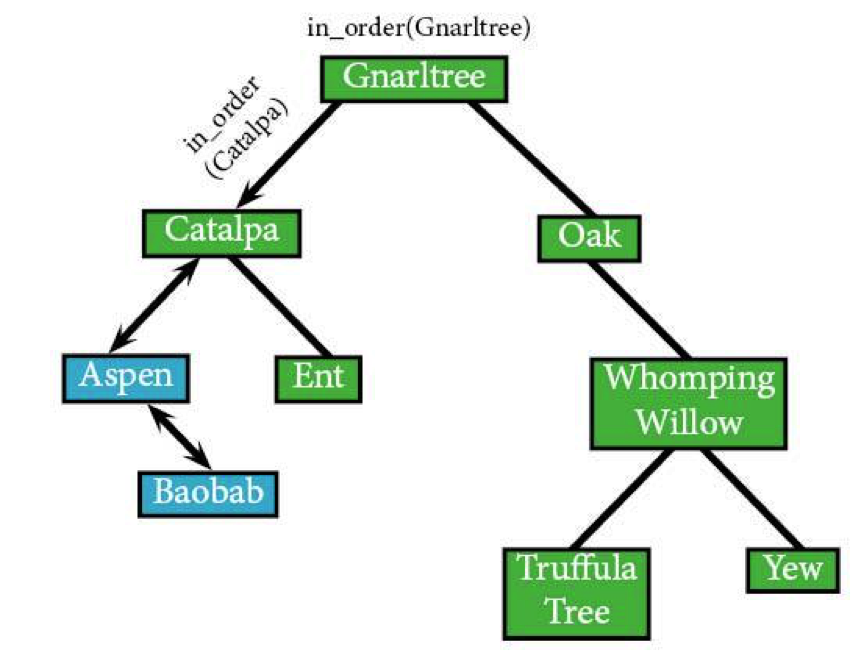
The algorithm's now done with everything to the left of Catalpa, which means it can visit Catalpa itself. Hopefully it brought a nice gift.

in_order(Catalpa)
	in_order(Aspen)	/*already been there, we're moving on*/
	IF Catalpa:
		visit(Catalpa)

 

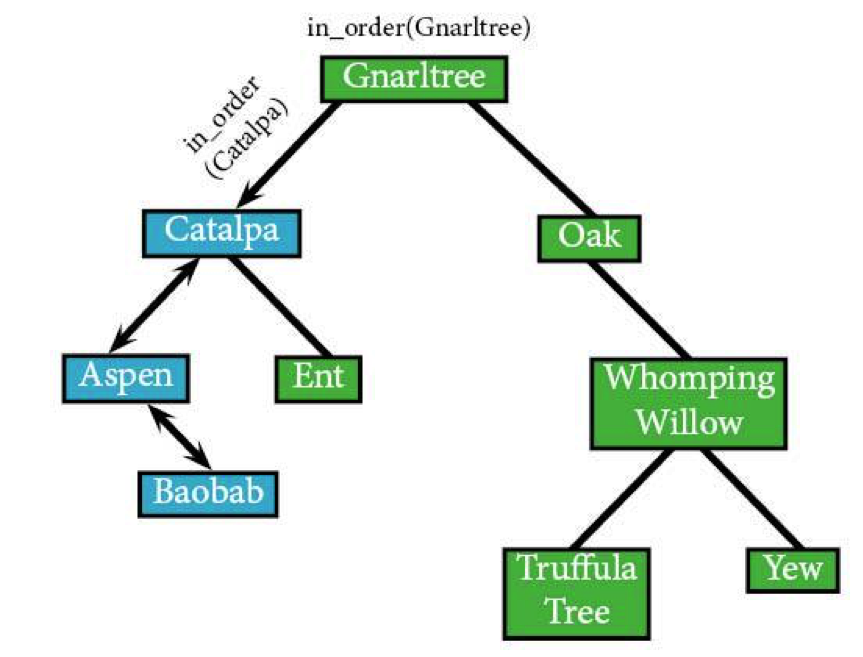
Once that's over, the algorithm's going to visit Catalpa’s right node: Ent.

 

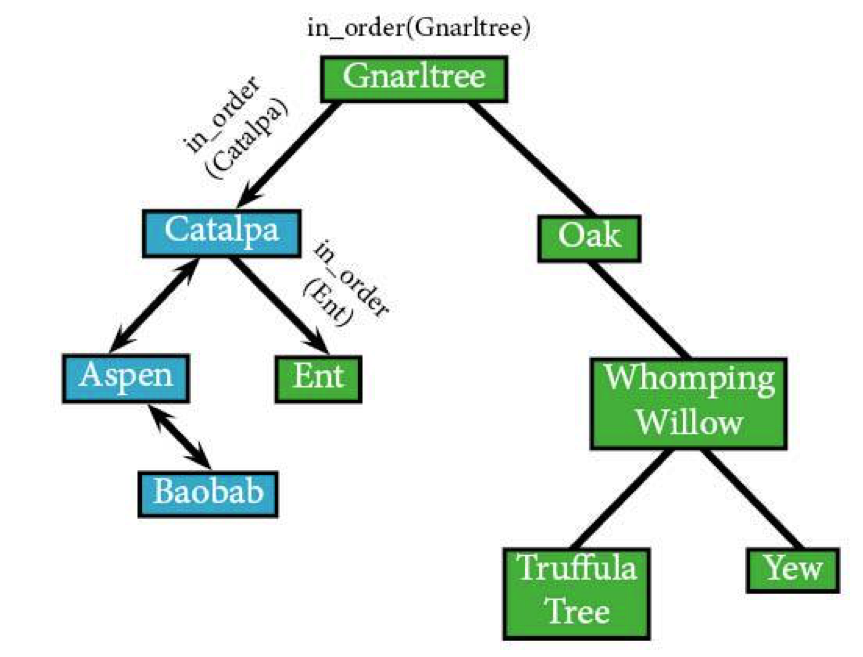
Ent doesn't have any left nodes, leaving the algorithm free to visit it.

in_order(Ent)
	IF in_order(NULL)
	ELSE
		RETURN
	END IF
	IF Ent:
		visit(Ent)

It also doesn't have any nodes to the right, which means the algorithm's headed back up to in_order(Catalpa).

 

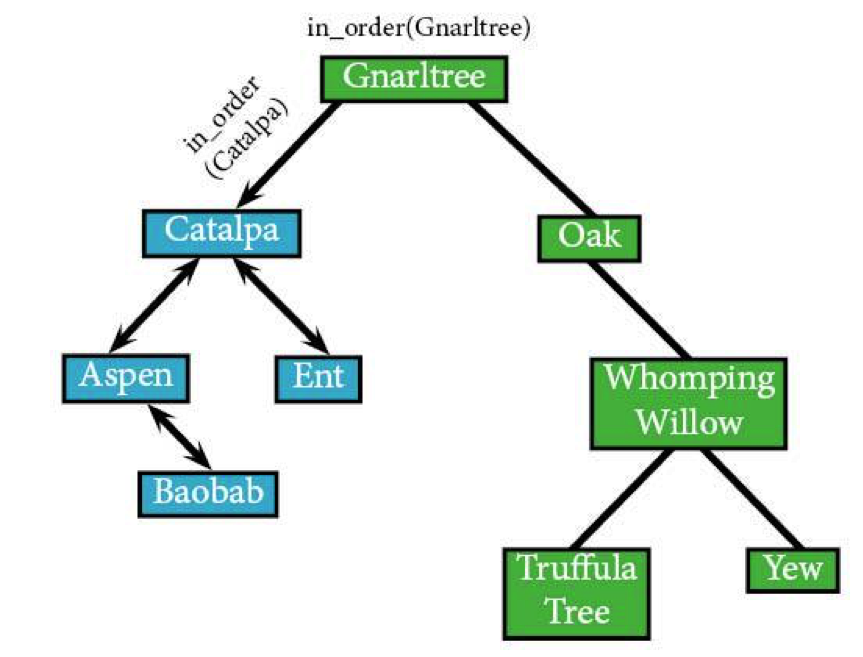
Now that we're back from both Catalpa's left and right subtrees, we can cross off everything under Catalpa as being checked, meaning that we can head back up to in_order(Gnarltree) and finally visit it.

in_order(Gnarltree)
	in_order(Catalpa)	/*already been there,*/
				/*ready for more nodes*/
	IF Gnarltree:
		visit(Gnarltree)

 

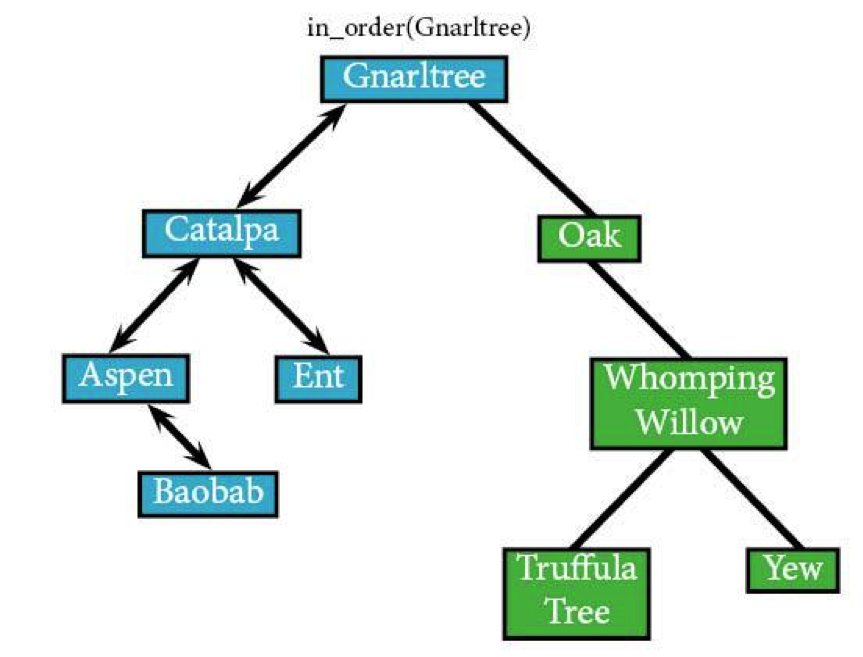
After Gnarltree, we'll travel down Oak and run in_order on it. Oak doesn't have any left-hand nodes, meaning the algorithm's going to skip straight to visiting it.

in_order(Oak)
	IF in_order(NULL)
	ELSE:
		RETURN
	END IF
	IF Oak:
		visit(Oak)

 

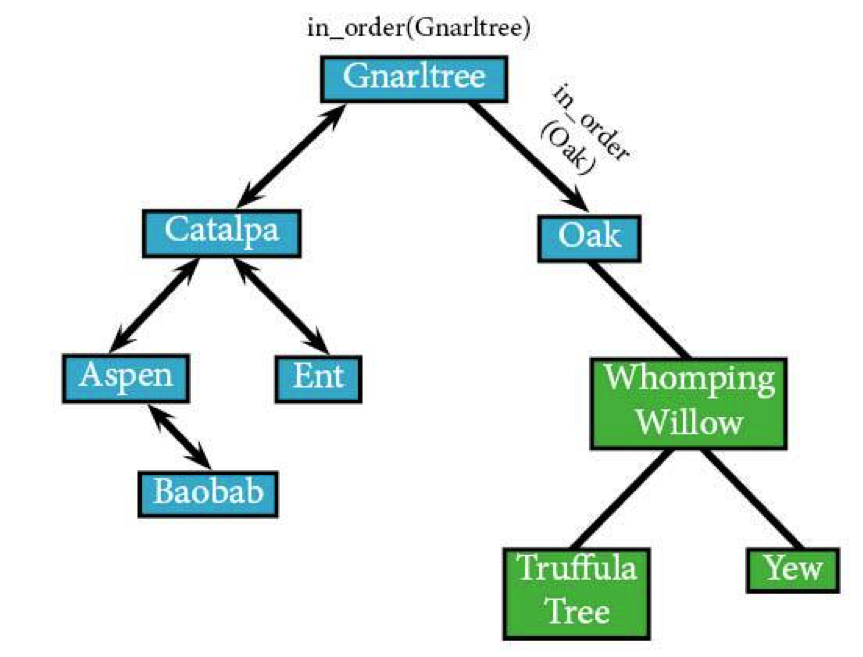
Then we run in_order on Oak’s only right-hand node, Whomping Willow (WW).

Whomping Willow does have a left-hand node (which itself has no children), meaning we'll skip it and head to that left child (Truffula Tree) as the next one to visit. Don't worry, Whomping Willow, we'll get to you.

 

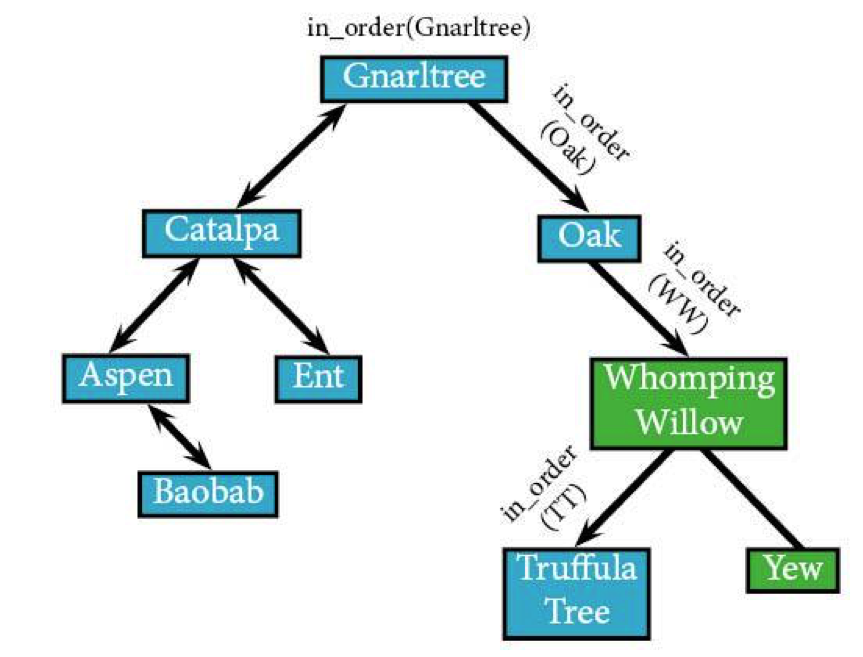
Truffula's pretty quick, since it's a leaf, meaning we'll bounce back up to Whomping Willow, and head right back down to Yew afterwards. Yew has no children, so we go straight to visiting it.

 

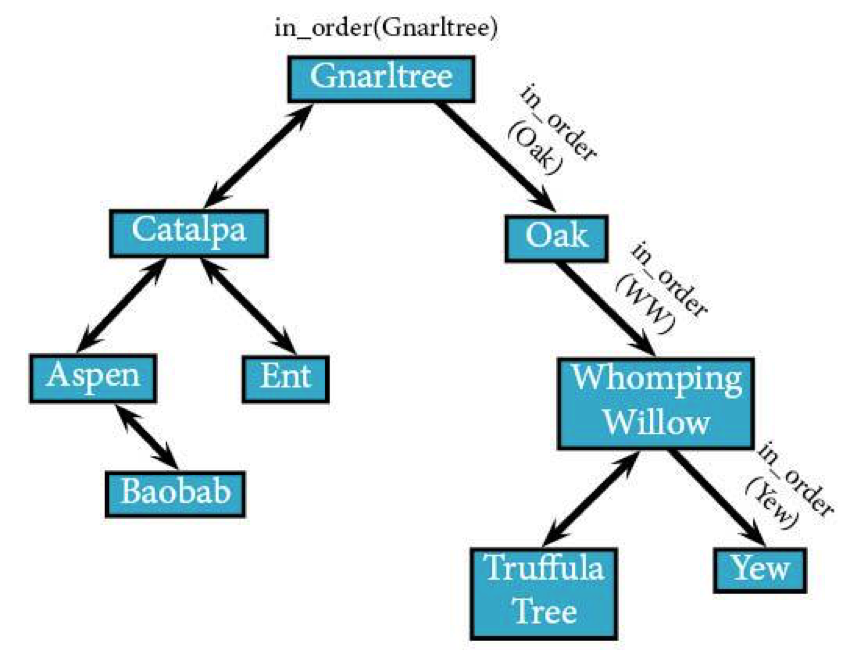
Since in_order(Yew) can now return, the algorithm's going to head back up through the tree and finish back at the root to return in_order(Gnarltree).

 

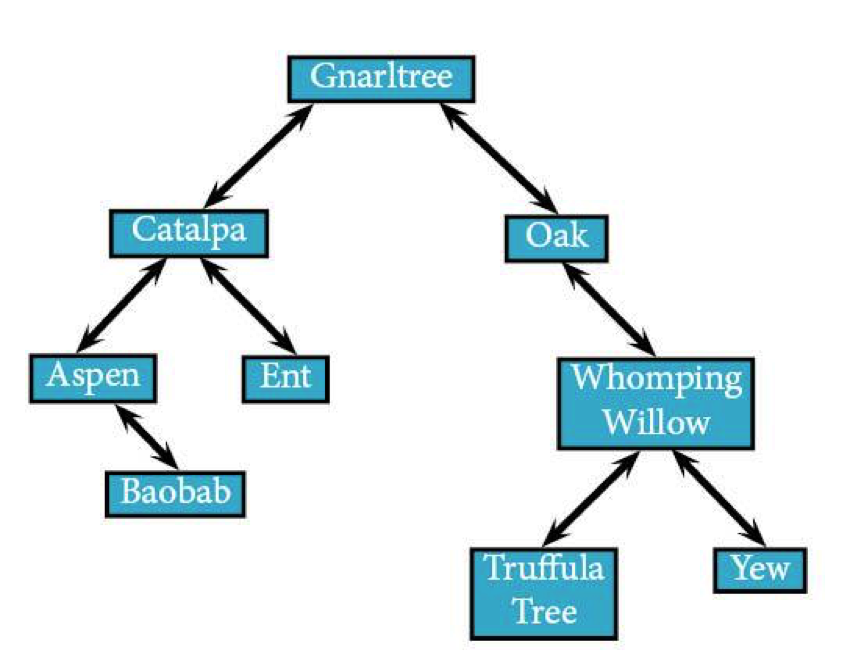
Here’s how it all went down for the in-order traversal:

Aspen → Baobab → Catalpa → Ent → Gnarltree → Oak → Truffula Tree → Whomping Willow → Yew.

Notice that Gnarltree is kind-of in the middle. You could say the algorithm visited it in-order instead of pre-order. You might also notice that everything came out in alphabetical order. As long as your tree is sorted like a binary search tree, an in-order traversal will always visit the nodes in order.

Imagine that.

Want to guess where the root ends up during post-order traversal?

Is the suspense killing you?

We thought so.