Self-balancing trees are marvels of computer science. Take that, apple trees. When implemented correctly, self-balancing trees balance themselves as they’re created, never needing any outside interference to look nice and balanced. All you have to do is set up that nifty, self-balancing structure when you first start adding data to your tree. Then you can sit back, relax, and re-watch Back to the Future. Your tree will take care of itself.

(Bet you've never seen an apple tree juggling its branches and apples like that.)

We could try to explain how it all works, but it’s really best to observe these trees in their native habitat. Keep quiet, don’t make any sudden moves, and maybe we’ll get to see a self-balancing BST in action.

You know, we don’t really like waiting. Let’s just make one.

We’ll use the numbers 34, 22, 17, 13, 37, 39, and 25 as nodes. At every step, the tree keeps track of each node’s subtree height, just like we did in the Balancing section. Once a node has a difference in its two subtrees of at least two (02 or 20), the tree's going to readjust and rebalance itself.

First comes the root node, 34.

 

If we throw 22 in, it'll become 34's left child. Because…22 is less than 34.

 

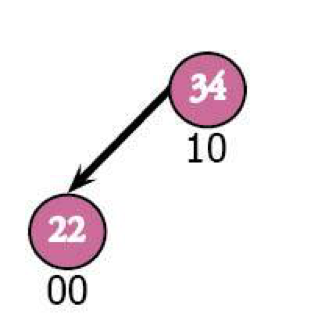
Next we'll throw in 17, which ends up as the left child of 22.

 

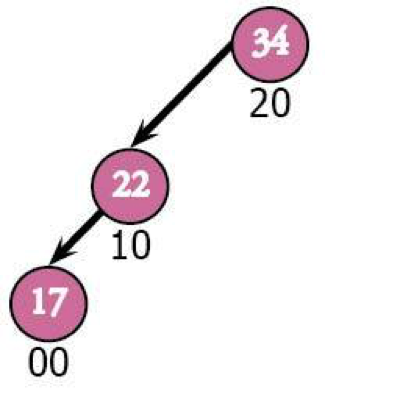
Uh oh. This tree has a problem. The tree's now unbalanced, which means it has to do something.

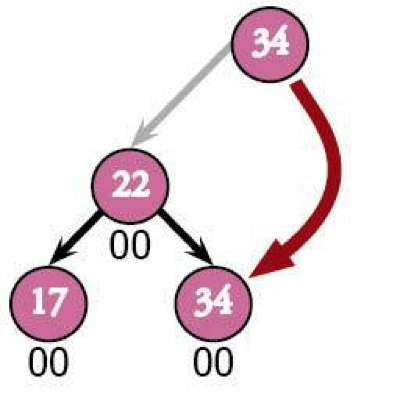
All you have to do is press the unpause button on your movie; the tree's going to do all the work by rotating its branches to rebalance itself. After the rotation's done, the tree will double-check to make sure everything is balanced.

The last node added (17) was the left-left descendant of the node with the super-unbalanced score (34). Since everything's to the left of the root, we know that logically the root could be a right child of either one. But because of the attachment between 22 and 17, we also know that it can't be 17's right child, since being 17's right child would mean being 22's left grandchild. 34's greater than 22, so it has to become 22's right child. It'll do something like this:

 

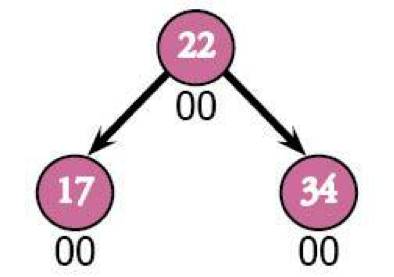
Boom. Perfectly balanced.

 

To make things interesting, let's throw in a nice, unlucky 13.

 

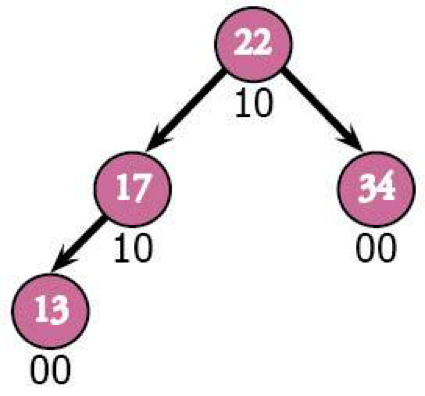
So far so good. Next comes 37, which goes into 22's right subtree as 34's right child.

 

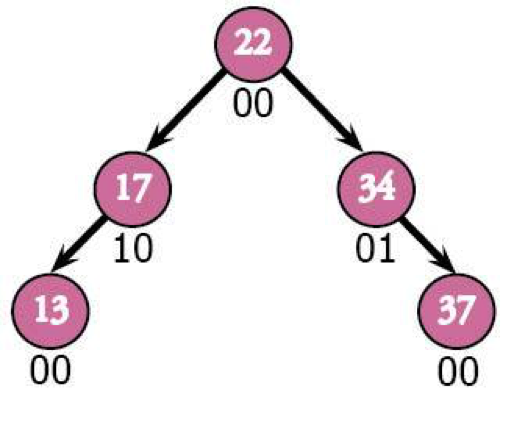
Here's where things get interesting. If we throw in 39 to the right of 37, we'll get some serious balancing issues.

[gulp]

 

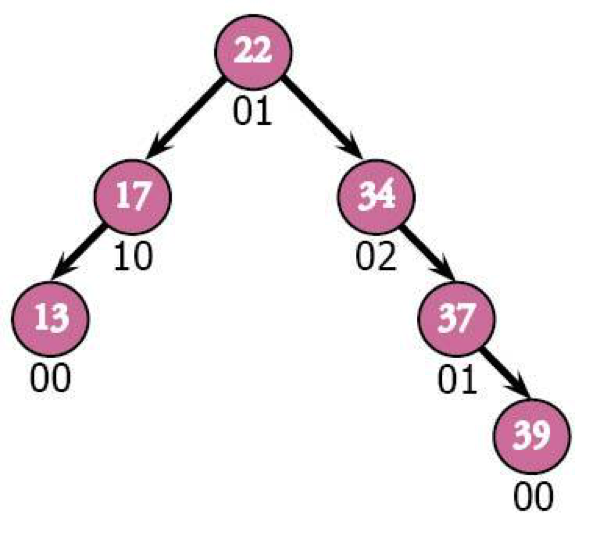
Here's where things get complicated. A subtree on the right is unbalanced, meaning that the tree's going to spring into action. We'll basically do the same thing as before, rotating that 02 node (34) so that it's a child of the 01 node (37). If you implement this type of tree, you'll need to be very careful about how nodes point to each other so that you don't lose anything when you juggle them.

 

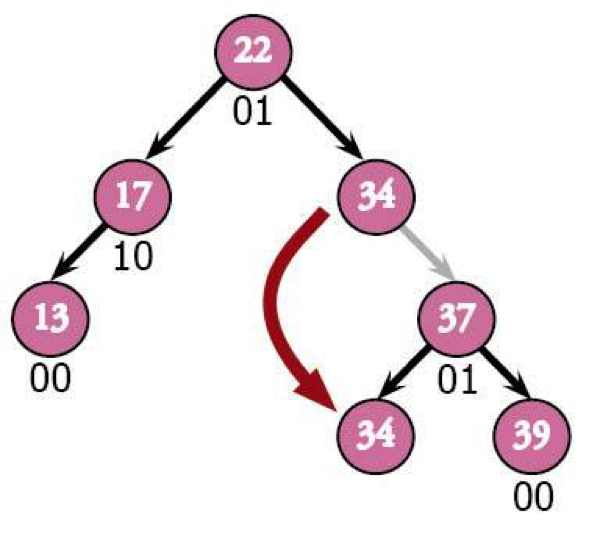
Just like that, we're balanced again. Only one node left.

 

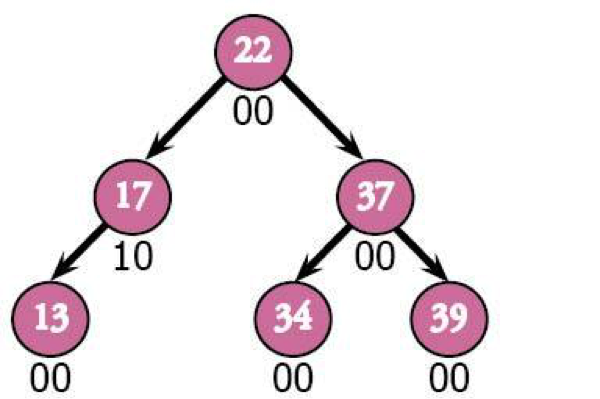
Let's throw in 25 just for good luck.

 

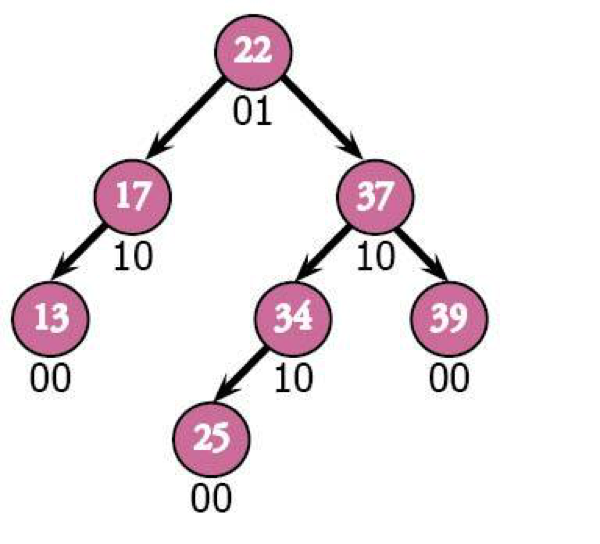
Phew! No more rebalancing needed. The tree's finished. Notice how it isn't the optimal shape? If we're really splitting hairs, the best possible tree would have a height of 2 instead of 3, but self-balancing trees are built to have random values added to them at any point. Taking the time to make this tree perfect would become useless the minute we add a new value. It's much more sustainable to just keep it from getting a little too unbalanced.

Basically balanced is good enough.

How Things Can Become Unbalanced

There are four different ways a node can unbalance a tree:

• left-left
• right-right
• left-right
• right-left

We've seen the first two, and they're usually the easiest, but any self-respecting tree (or its programmer) can also handle the left-right and right-left cases.

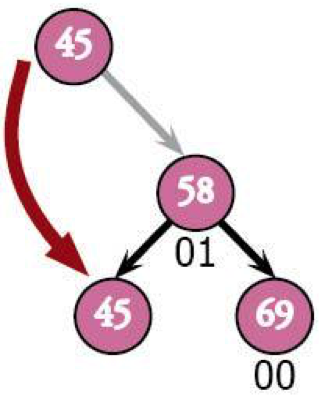
Say we've got this right-left situation. 58 was the most recently added node:

 

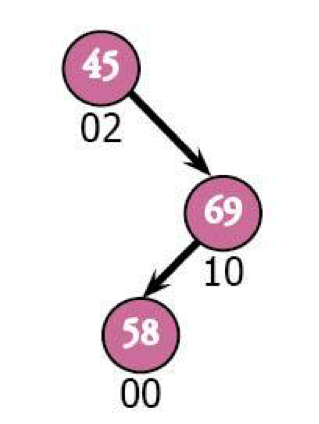
The easiest thing to do is make this look like a right-right case instead of a hairy right-left. To do that, we'll just switch 69 and 58 so that 58 is the parent.

 

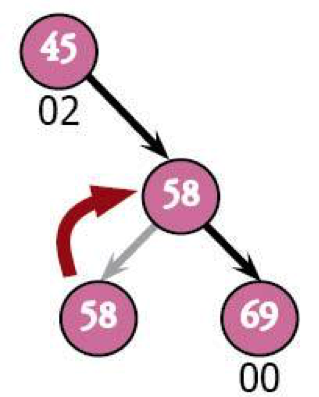
Now that we're in a state we've seen before, we can just treat it like that previous case. that means turning 45 into a child of the new root: 58.

 

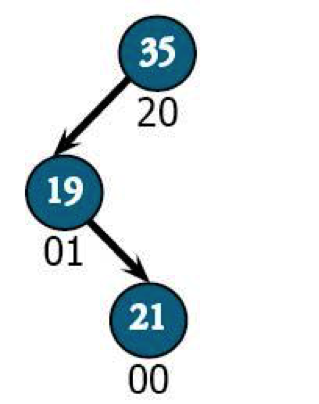
Left-right is going to follow a similar formula, but mirrored. We have a root of 35, with a left child: 19. 19's right child, 21, was just added in.

 

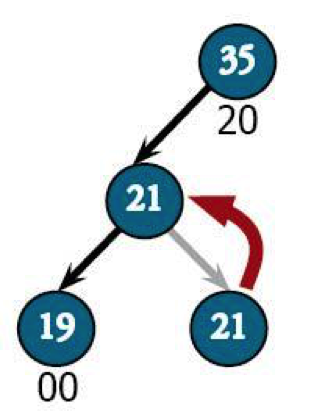
The easiest fix is to turn this into a left-left problem by making 21 the parent of 19. That way, we'll have a situation we already know how to deal with.

 

Now we're free to apply that left-left correction, making 21 the new root and 35 its right child.

 

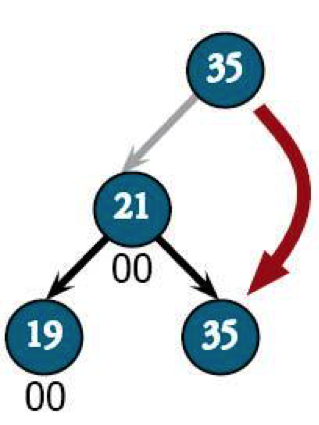
Done.

Self-balancing makes things convenient, but it can also cost a lot of time to maintain through the life of the data structure. Between balancing and checking to make sure it's balanced, depending on how big your tree gets and how often you need to find different nodes, it might not be the most efficient way to go.

You've been warned.

(Source 1, Source 2)