Graphs: Walking the Graph
Graphs: Walking the Graph
Say you just got the latest version of Save Alexandria, an RPG about the Library of Alexandria. It's got everything you could ever want in a game:
- Fire
- Hardcore parkour moves
- The inevitable destruction of everything you hold dear, leading to a crippling depression over the loss of so much knowledge
Long story short: it's great. The library's a labyrinth of bookshelves and fire, and your job is to get as many books and scrolls out as possible before the whole building collapses. To do well in the game, you have to know where the best books are and the shortest path out of the library at all times.
That's no easy task, but you have graphs on your side. Whew.
You've been through the library before a few times (okay hundreds of times), so you know just about where everything is. All the important books, at least.
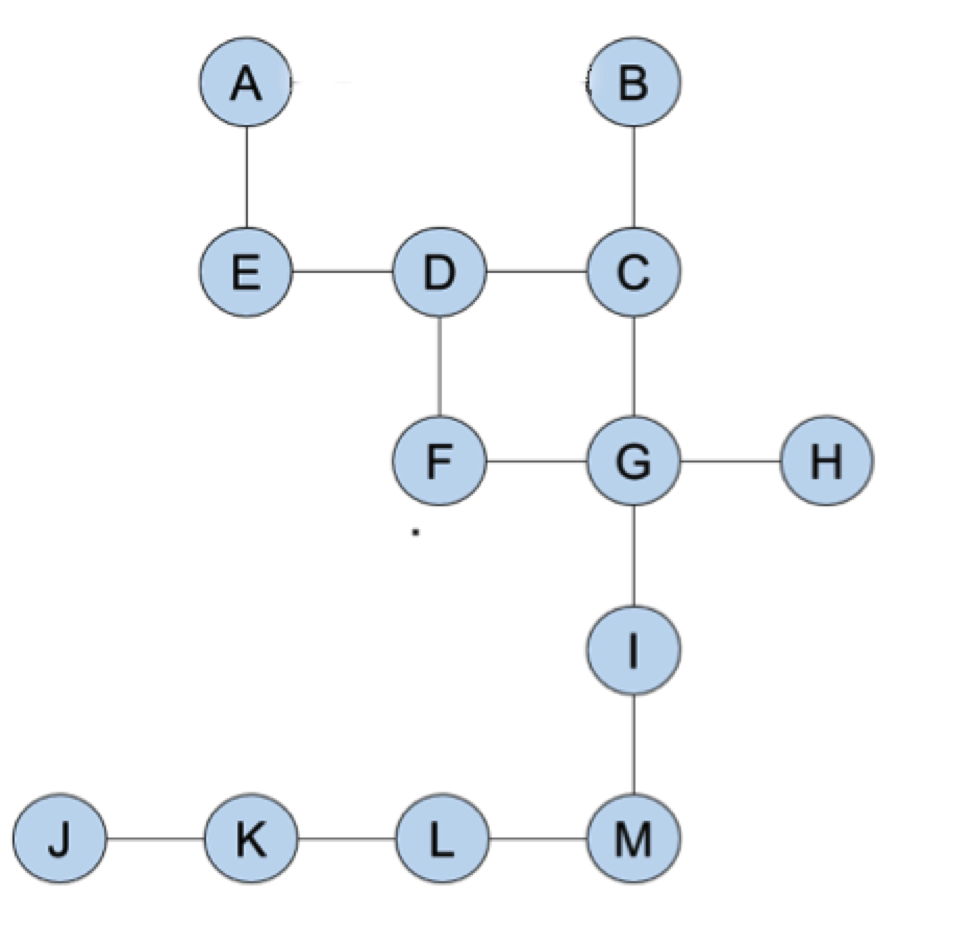
Here's a map of a piece of the library.

Each white block has an important book, which we won't include, but we'll put their initials in the right spot here.

What a happy coincidence that those totally-not-made-up books go in alphabetical order (according to English) on the map. Anywhere, there are two exits: H and J. You can make a graph to show the diagram:
Say you've got book A and need to get to the exit at H. What's the fastest way to do it? You can figure it out one of two different ways, but they can give you very different results.
Breadth-First Search
Breadth-first search is all about control at every step of the wild ride through the Library of Alexandria. When you use this search, you're taking a path one step at a time, checking to make sure you follow every possible path. It's like using Calvin's duplicator to make a copy of yourself every time you see a new fork in the path. First, let's establish some ground rules. A node can be one of three states:
- Undiscovered
- Discovered but not explored
- Explored
To follow a breadth-first search (also known as a BFS, to those in the know), you
- take a node and look at every node that node's connected to.
- add those nodes to a list.
- check the nodes each node is connected to.
- add them to the list.
- check the nodes connected to the nodes connected to the starting node.
- rinse, repeat.
At every new branch in nodes, you're making a copy of yourself to search down that new path. In computer science terms, that means adding the node to a list. What you'll do is check each item in the list in the order you find it. You know what, let's follow our path in the Library in Alexandria to get a better sense of what's going on.
Step 1: Start at Node A
We're going to start with a list of one element: Node A.
| Index | 0 |
| Value | A |
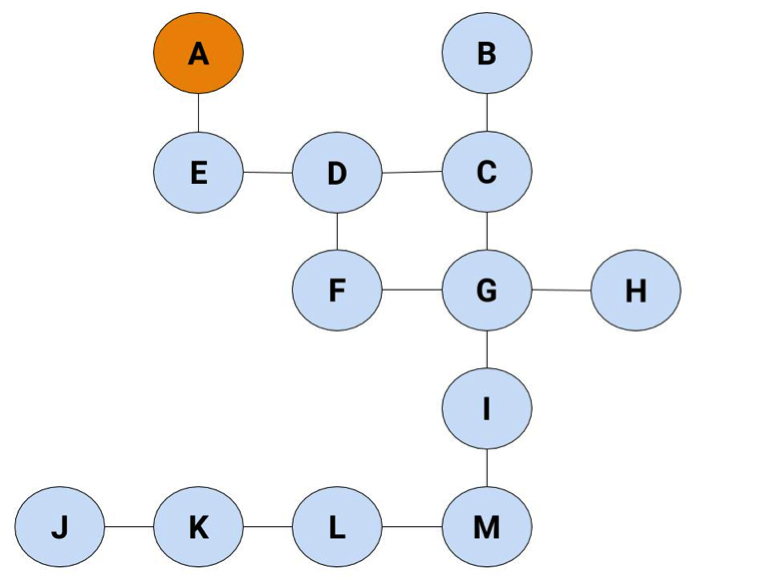
You've found A, but you haven't searched it yet. Searching means finding all the nodes it's attached to, which is the next step. Here you only have one choice: find and go to E.
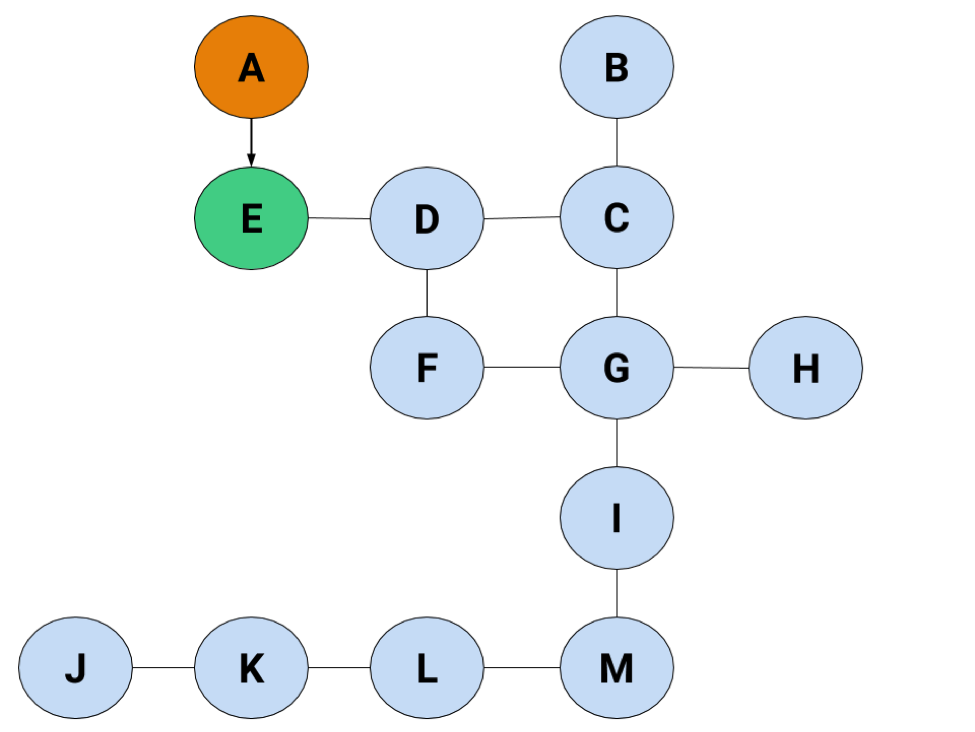
Alt. text: The graph, with A highlighted in orange and E highlighted in green.
E's in green because it's been found but not searched. The list now looks like this:
0 1
| Index | 0 | 1 |
| Value | A | E |
After that, the only option's to head to D, but now we're about to have trouble.
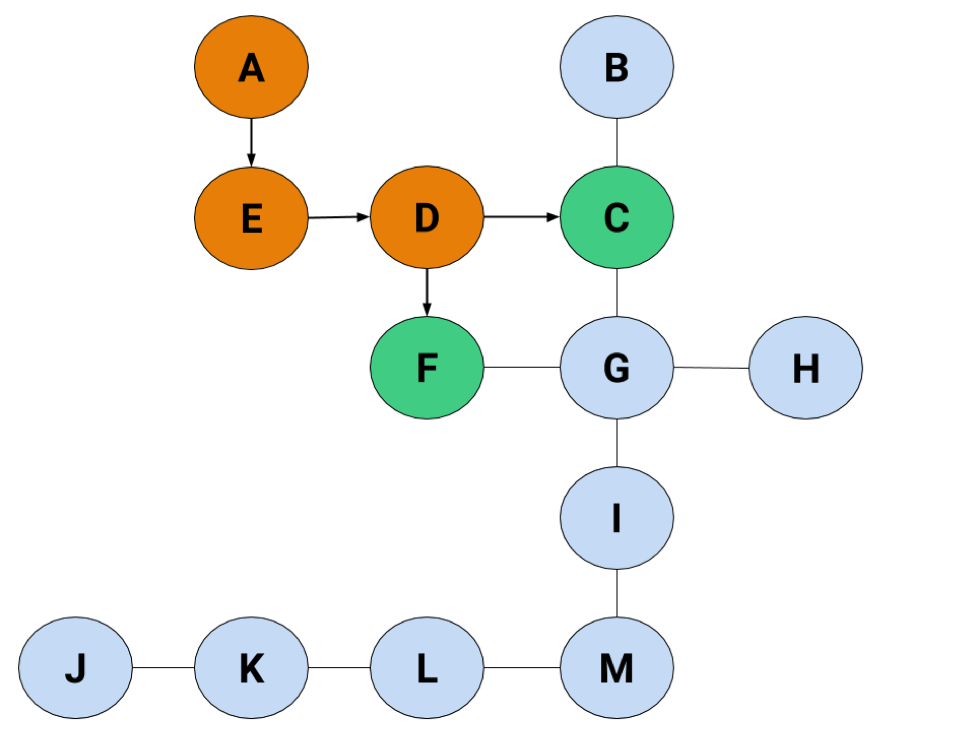
D can lead to either C or F, and we have no reason to know which one's going to be better at getting us to H. Some algorithms might ask you to just pick one and roll with it, but not the BFS. The BFS wants to be sure you've taken the right root. So…it's going to check both C and F at the same time by adding them to the list:
| Index | 0 | 1 | 2 | 3 | 4 |
| Value | A | E | D | C | F |
Because we arbitrarily added C first, we're going to check it before F, giving us something like this:
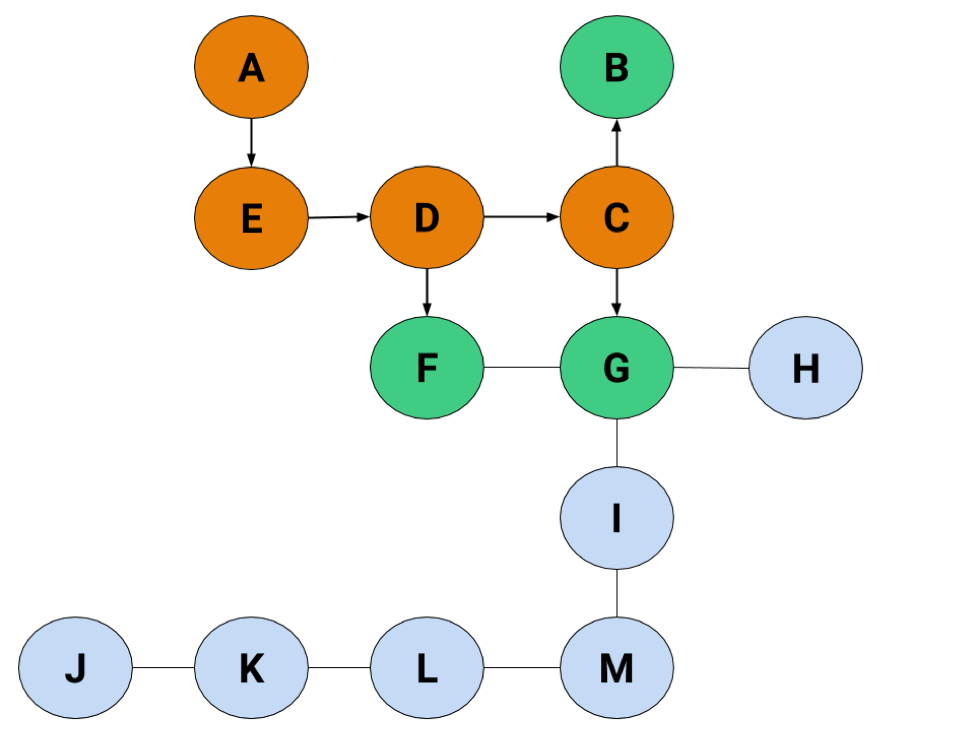
Now our list looks like this:
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Value | A | E | D | C | F | B | G |
C's checked, which means we can move on to F, except there's one problem: now that G's been "found," there aren't any new nodes for F to discover. That makes it basically a dead end, so we'll need to move on without adding any nodes to the list.
Sigh
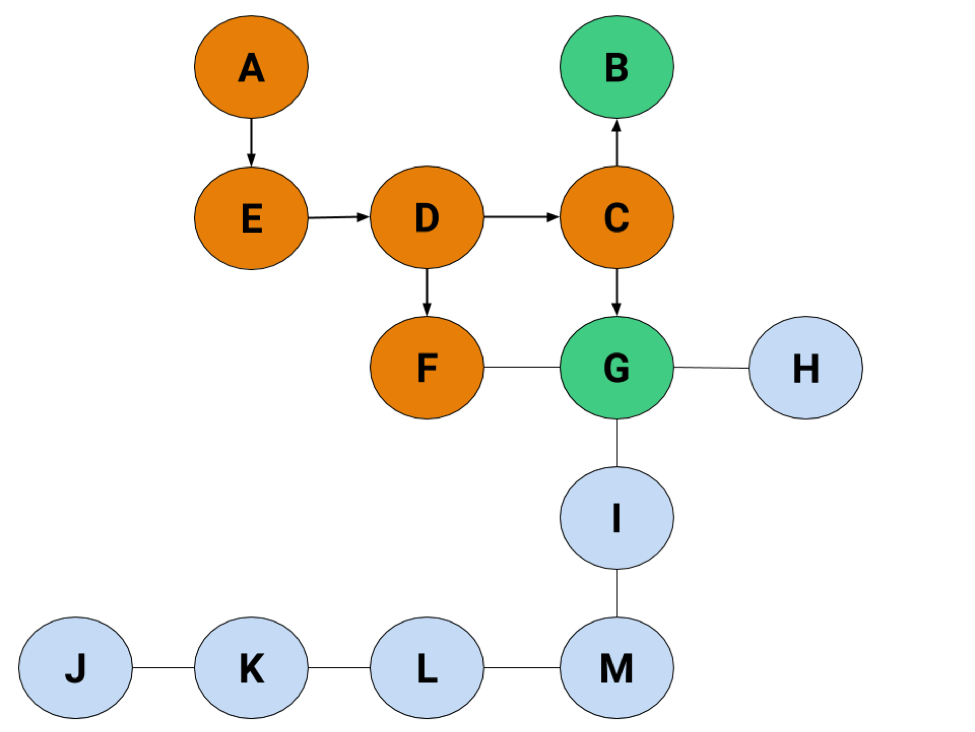
Due to our arbitrary decision to pick the left before right, B's also going to turn into a dead end before we look at G.
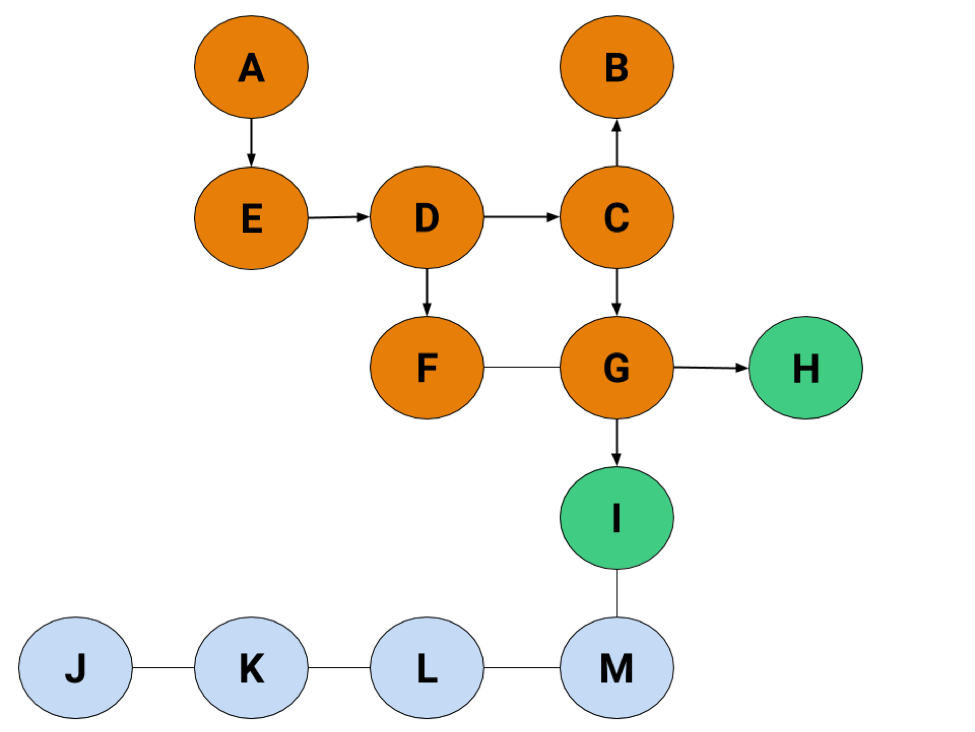
From G, we've found both H and I, but our end condition can't be reached until we actually search H. Now our list looks like this:
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Value | A | E | D | C | F | B | G | H | I |
The final step just looks like this:
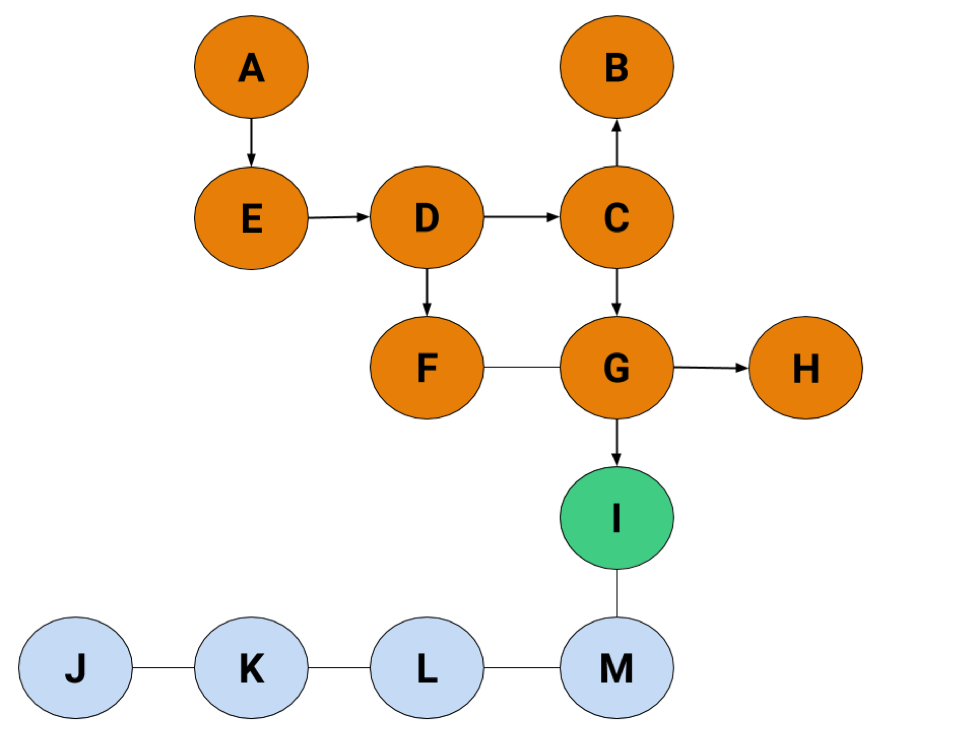
Making the final path:
A → E → D → C → G → H
Problem solved.
In pseudo-code, that means you'll need to use a queue, which lets you take out the first things you put in. Just like the line for your favorite amusement death-defying roller coaster, the number of people in front of you is equal to the number of people you'll have to wait for before you, too, can enjoy the controlled masochism of feeling like you could die but probably won't. Queues do the same thing—minus the death-defying flips. Or the headache afterward.
But they wait in line for their turn when they're put in a queue. That's known as a First In, First Out (FIFO) structure in CS.
When we add something to a queue, we're enqueue-ing it. To remove it, we'll need to deque it. (It's pronounced the same way as "decking someone in the face." Coincidence? We think not.)
Depth-First Search
If breadth-first search is all about control and careful planning, sending copies down the different paths till we find the solution, depth-first search is all about running headlong into the labyrinth and running back when we hit a dead end. For everyone whose duplicator is on the fritz, or, you know, can't physically make a copy of themselves because they don't live in a fictional world, this is probably the only option.
Again, we'll say the exit's at H, and we're starting at A.
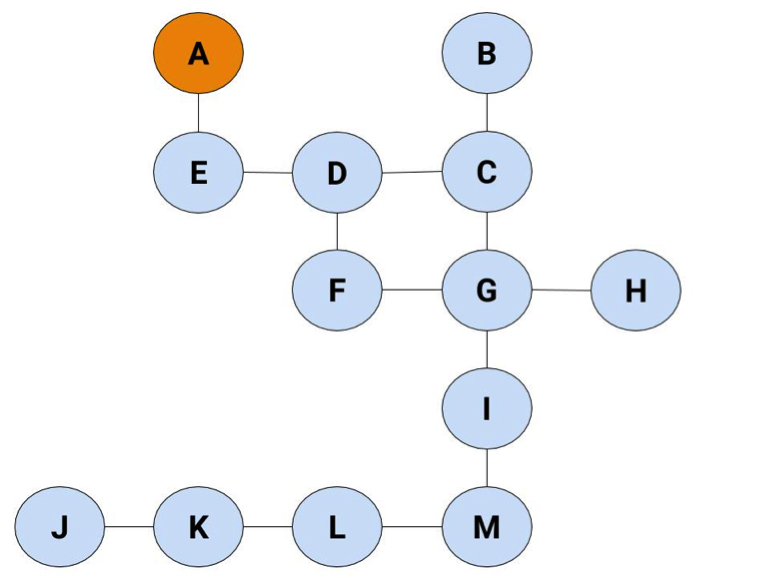
We'll skip a couple of steps this time to get to the interesting node: D. Otherwise, there's a bunch of copying from the last method and it looks virtually the same till that point.
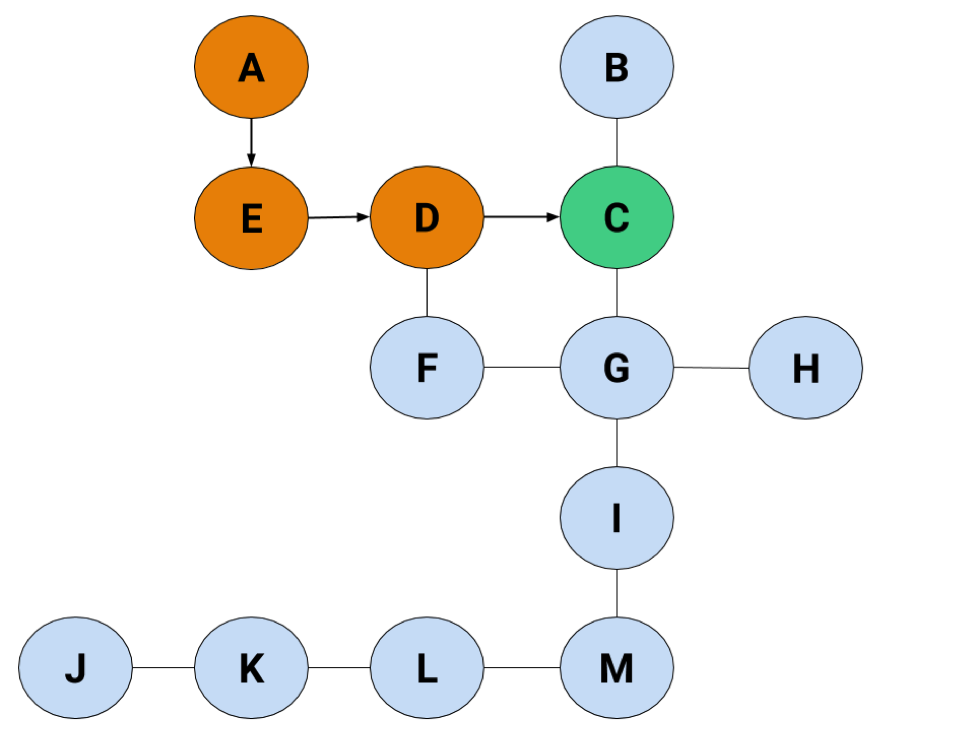
Instead of holding onto both C and F, we're only following C to see what happens. Taking our arbitrary pick-the-left method—a truly sinister choice—we'll take C to B, like this:
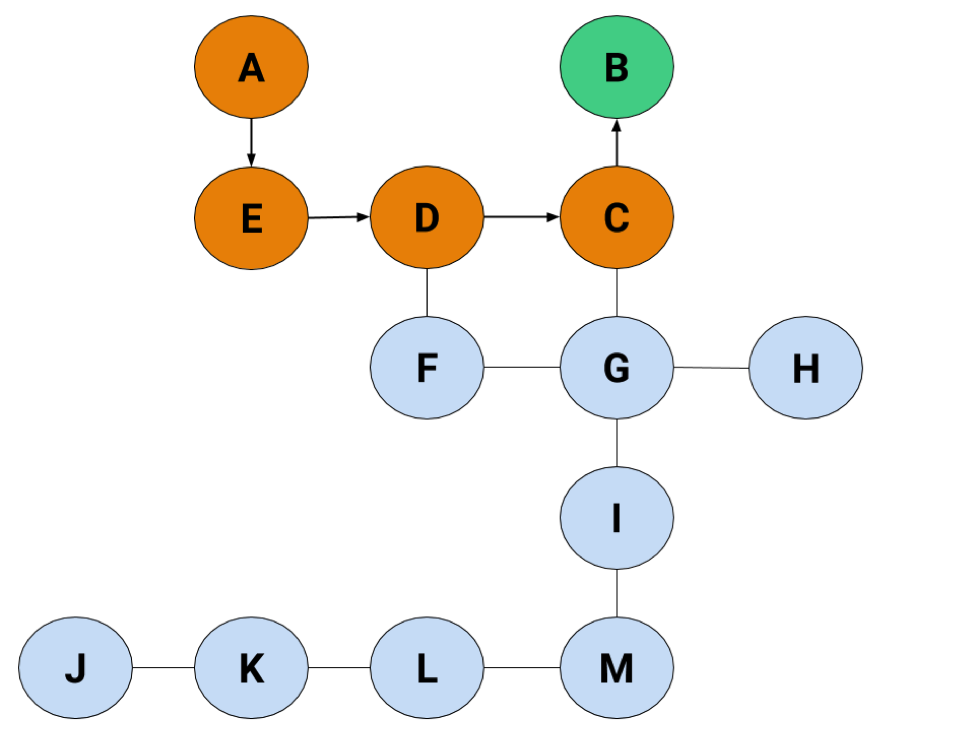
But…B's a dead end. We have nothing on the radar to go off of now that we've hit a dead-end. We have a couple of options in what we could do. Either
- give up and stomp away (the classic burn your bridges approach to life).
- admit maybe we made a wrong turn and jump back to the last node (the classic oops, let's try again approach to life).
If we jump back to C, we'll find there's a route we haven't taken, but if there wasn't, we'd keep jumping back until we found a node connecting to another node. Once we jump back to the starting node without ever being able to find another node, that's when we know there isn't a path we can take to wherever we need to go. Anyway, let's jump back to C for now.
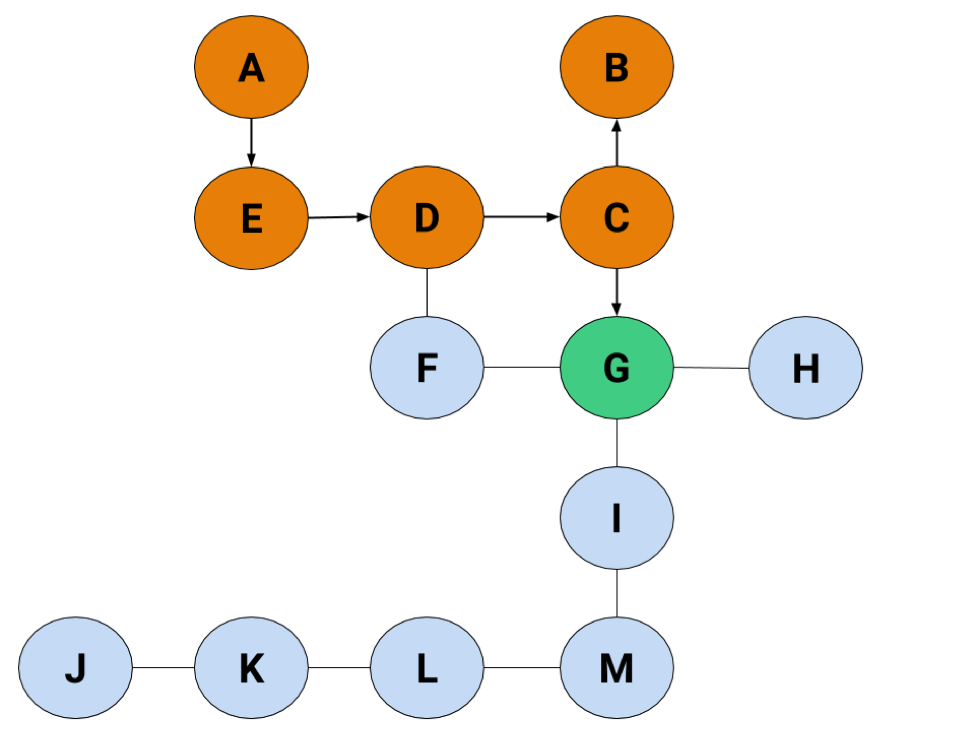
Now we're back in action. There's just the final step of picking the left node, and we've found the exit.
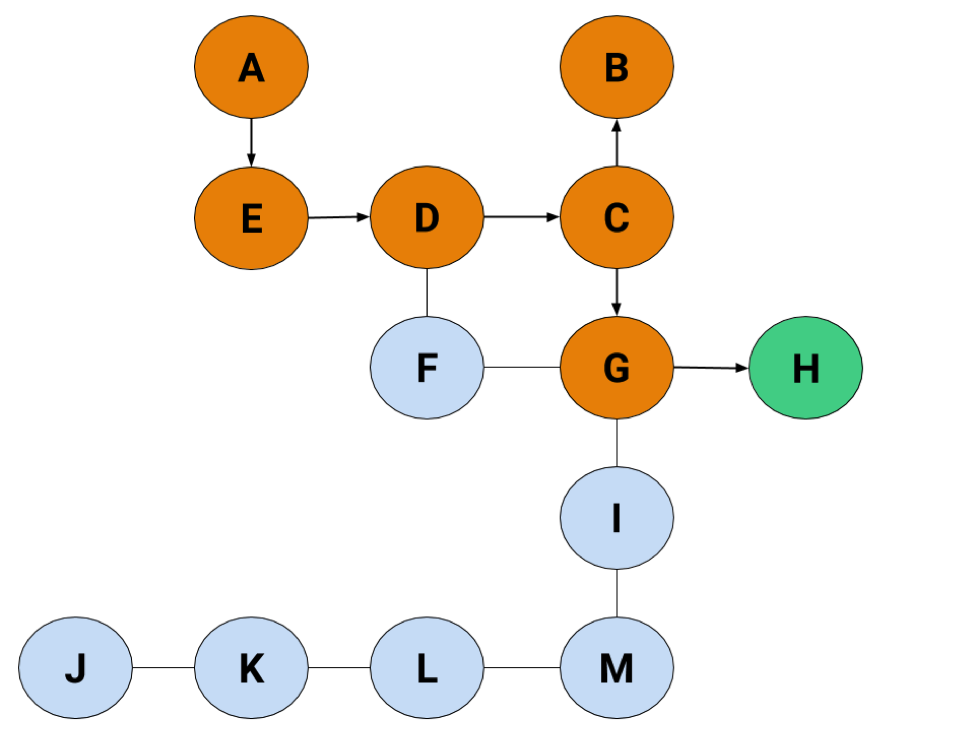
Boom.
Even though we had to jump backwards, using the DFS saved us some time by not having to search F. Even so, you'll have to be careful with this search because it could send you
- into a giant loop around the graph without finding what you need.
- into a path that gets to the end node, but with a lot more steps than you need.
The BFS is an exhaustive search, but it's guaranteed to get you the shortest path. The DFS can take less time and energy, but it won't always get you the fastest path—or even a single path. So be careful deciding between them, Shmooper.
When actually making a DFS, you'll always need a stack. Just like in the real world, putting things like
- fine china
- shirts
- issues of Nat Geo
into a stack means that you'll have to take off the last things first to get to the thing you want (unless you don't mind a floor covered in shards of glass, formerly clean laundry, and crumpled magazines). In contrast with a the queue, this structure's called a LIFO (Last In, First Out).
Adding something to the top of the stack is called pushing it. The reverse operation, popping, happens when you take the last item off.
Stacks are great at simulating that jump back moment before. If we add every searched element to a stack and hit a dead end, we pop the last element off, jumping back to the element before it. If that one doesn't have another place to go, we'll pop it off, too, continuing until we can find a new path (or we find that there isn't one).
And that's all there is to it.