Periodicity and Symmetry Examples

What angle between 0 and 2π is coterminal with ?

To bring an extra large angle down under 2π, we need to subtract 2π again and again, no matter how many times it takes to get there. Our fraction has a denominator of 4, so we'll really be subtracting out 

We only had to subtract once. The angle between 0 and 2π that is coterminal with  is .

Find .

The sign and the actual value of trig functions are independent, so we can find each one separately. Positive  is the same as 30°, which is in the 30-60-90 triangle. Reaching deep into the Shmoop mental archive, we remember that:

 = ½

Now for the sign. Cosine is an even function, so cos(-x) = cos x. That means it is the same as cosine. Problem done.

Find .

We've got our work cut out for us on this one. We'll simplify this a little bit by noting that cotangent is odd.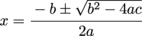

We'll look for the positive angle, then swap our result around to the other sign. But enough about that for now, let's focus on finding . To do that, we need to find tangent first. We're really getting the run-around on this problem.

If we look at , we see that it is greater than  but less than π. Let's find the reference angle—how far away the angle is from π or 2π, whichever is closest. In this case, we're going for π: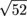

Hey, we know that angle. That's 60°, which is part of the 30-60-90 special triangle. Peering into its triangular depths, we pull out that .

We'd like to say the problem is done, but we were actually looking for cotangent of this angle. We have to reciprocate, by flipping the fraction upside down.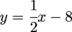

There's still more. Last but not least, we need to worry about the sign. We're not looking for but rather . We already decided that this means our answer is negative, so let's slap that negative sign on and be done with it: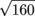

Whew. That was a toughie. Sometimes a trig problem will keep going and going. We have to remember to always check our answer against what the problem actually asked for, or else terrible things will happen. Even more terrible than working on trig problems.

Find .

Rules are rules, secant, and they apply just as much to you as they do to cosine. We don't care if your father is the principal, you're an even function, so sec (-x) = sec x. That means we're really looking for .

Speaking of cosine, we need its help to find out anything about secant, because they are reciprocals. And we know, from the special angle triangles, that  equals . Time to flip it, flip it good.

Yuck, a radical in the denominator. That won't do at all; what if the neighbors saw it? A quick cleanup gets an answer of , our final answer.