We know the sine function is in the form of y = Asin (Bx + C) + D, we just need to figure out the values of A, B, C, and D. Grab your deerstalker cap and magnifying glass, and let's get to the bottom of this mystery. The midline, D, is the easiest variable to track down. The maximum value of the function is at y = 0 and the minimum value is at y = -4. Midway between them is the midline (whoda thunk), and it is at y = -2. This means D = -2. Next up is A, for apple, adamantium, and amplitude. That last one is how far the maximum and minimum values are from the midline. We now know they are 2 away, so A = 2. Whooah, we're halfway there! Whooah, livin' on a prayer. Take my hand and we'll make it I swear. The period of the function only depends on B, while the amount of horizontal movement depends on both B and C, so we'll take a look at the period next. It is the length of a complete cycle of the curve. Looking at our curve, we see that it takes 2π to get back to the beginning of the curve, so our period is 2π. If the period is 2π/B, B must be 1. Moving on to B, we know that the period of our function is  , so if we know the period, we know B. Looking at our curve, we see that it takes 2π to from one peak to the next, so our period is 2π. If the period is , so if we know the period, we know B. Looking at our curve, we see that it takes 2π to from one peak to the next, so our period is 2π. If the period is  , and it is, B must be 1. , and it is, B must be 1. Now that we're looking at the horizontal position of the graph, it looks a lot like cosine. The maximum on the y-axis is at x = 0, while the basic sine function has a maximum at  . This shows a horizontal shift of . This shows a horizontal shift of  to the left. That means that to the left. That means that  (the amount of horizontal movement) equals (the amount of horizontal movement) equals  . Let's solve for C: . Let's solve for C: 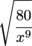
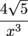
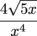
We've tracked down all the values. A = 2, B = 1, C =  , and D = -2, and we can plug these in to the equation y = Asin (Bx + C) + D to get: , and D = -2, and we can plug these in to the equation y = Asin (Bx + C) + D to get: 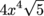
| |