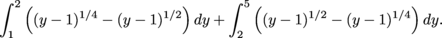Area, Volume, and Arc Length Exercises

Answer

First graph y = cos x and :

Then shade in the region between these two graphs on the interval . This is the region R:

(a) With vertical slices, we have slices of width Δ x. Since the graph of y = cos x is above the graph of  on this interval, the height of the slice at position x is

This means the area of a slice is

We were told to look at the interval . The integral expression

gives the area of R. Alternately, since the region R is symmetric with the y-axis as its line of symmetry, we could find the area of half of R and then multiply by 2. The expression

also gives the area of R.

(b) A horizontal slice of R looks like this:

The thickness of a slice is Δ y. The width of the slice at height y is approximately twice x, where (x,y) is the point on the graph of y = cos x that lies at the right edge of the slice.

If y = cos x then x = arccos y, so the width of a slice is

2x = 2arccos y.

The area of the slice is then

2arccos y Δ y.

The values of y that make sense are from  to y = 1.

The area of R is

Answer

It's always best to start with a drawing of the region. The region R looks like this:

The curve y = x⁴ intersects x = 2 at the point (2,16) and intersects the line y = 81 at the point (3,81). Knowing these points will be useful for figuring out limits of integration.

(a) A vertical slice of R looks like this:

The height of the slice at position x is 81 – x⁴.

The area of this slice is

(81 – x⁴) Δ x.

The values of x that make sense are 2 ≤ x ≤ 3.

So the area of R is

(b) A horizontal slice of R looks like this:

The slice at height y has width x – 2 where (x,y) is a point on the graph of y = x⁴.

If y = x⁴ then x = y^1/4, so the width of the slice is

x – 2 = y^1/4 – 2.

The area of the slice is

(y^1/4 – 2) Δ y.

The values that make sense are from y = 16 to y = 81.

Adding up the areas of all the slices and letting the number of slices approach infinity, the area of R is

Answer

The region R is a quarter of a circle of radius 1:

(a) A vertical slice of R looks like this:

The thickness of the slice is Δ x, and the height of the slice at position x is y, where (x,y) is on the graph x² + y² = 1. This means

The area of the slice is

Since x can be anywhere between 0 and 1, the area of R is

(b) Slicing horizontally doesn't change things much in this case. A horizontal slice at height y has thickness Δ y and width 

The area of such a slice is . Since y also ranges from 0 to 1, the area of R is

Answer

The region R looks a little something like this:

Within the region R, x goes from 0 to 3 and y goes from 1 to e³. These will be our limits of integration later.

(a) A vertical slice of R looks like this:

The height of the slice at position x is (e^x – 1), so the area of the slice is (e^x – 1) Δ x. Using the limits of integration we found earlier,

the area of R is

(b) A horizontal slice of R looks like this:

The width of the slice at height y is

3 – x = 3 – ln y

so the area of the slice is

(3 – ln y) Δ y.

Using the limits of integration we found already, the area of R is

Now matter how we slice and dice the region, the area should be the same.

Answer

The region R can be drawn like so:

Since R is symmetric across the y-axis, we can find the area of the part that's in quadrant 1 and then multiply by 2 to find the full area of R.

The vertical slice of R at position x looks like this:

The height of this slice is

and the area is

As x can go from 0 to 1, the area of the right half of R is

and the area of all of R is

If we wanted to find the area of all of R at once, x would go from -1 to 1 and the area of R would be

Answer

The region R looks like this:

Using horizontal slices, the slice at height y stretches from the graph of  (or x = 2y) on the left to the graph of y = 5 – x² (or ) on the right:

The width of this slice is , and the area of the slice is

In the region R, the variable y ranges from 0 to 1:

Taking the integral, the area of R is

Answer

The region R looks like this:

This problem is very similar to the previous one, except that now the horizontal slice stretches from the graph of y = 5 – x² on the left to the graph of  on the right.

The width of the slice at height y is now , so the area of that slice is

The variable y ranges from 1 to 5, so the area of R is

This was a great problem to do with horizontal slices. With vertical slices we would have needed two separate integrals, since the bottom of a vertical slice changes from y = 5 – x² to y = ^x⁄2 at the point (2, 1).

Answer

The height of a slice is :

The area of a slice is

The variable x measures the position of the slice on the x-axis, and x ranges from 1 to 4.

The area of R is

When we go beyond finding area to finding mass, pressure, or the volume of the Batmobile, we'll need to think about things besides the shape of the region when deciding which way to slice. We're having you practice slicing every-which-way now so you'll be comfortable slicing every-whatever-way later.

Answer

The region R looks like this:

Earlier, we wrote an expression for the area of R using horizontal slices.

To use vertical slices, we have to split R into two pieces. The piece on the left is bounded by the graph of , the line x = 2, and the x-axis. The piece on the right is bounded by the graph y = 5 – x², the line x = 2, and the x-axis. Let's look at the piece on the left first. The slice at position x has height , and x runs from 0 to 2. The area of the piece on the left is

For the piece on the right, the slice at position x has height 5 – x², and it x runs from 2 to  (since this is where the graph of 5 – x² crosses the x-axis).

The area of the piece on the right is

Adding up the areas of the two pieces, the area of R is

Answer

The region R looks like this:

We found an expression for the area of R using horizontal slices earlier.

To use vertical slices, we have to split the region into two parts at x = 2. The left piece uses the graph y = 5 – x² for its lower bound, and the right piece uses the graph of  as its lower bound.

The limits of integration will be the same as in the previous problem. The left piece has x going from 0 to 2, and the right piece has .

A slice of the left piece has height

5 – (5 – x²) = x².

Taking the integral, the area of the left piece is

A slice of the right piece has height .

Taking the integral, the area of the right piece is

Adding the areas of the two pieces together, we get a nice integral-y expression for the area of R:

Answer

The region R looks like this:

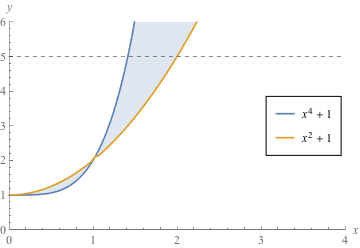
(a) With vertical slices we have to split up the region into three pieces!

The graph y = x⁴ + 1 intersects the line y = 5 when . The graph y = x² + 1 intersects the line y = 5 when x = 2.

1) For 0 < x < 1 the graph of x² + 1 is on top.

2) For  the graph of y = x⁴ + 1 is on top.

3) For  the graph of y = 5 is on top.

This means there are three pieces whose areas we need to find.

Let's look at the left piece, where 0 ≤ x ≤ 1.

The height of a slice at position x is

(x² + 1) – (x⁴ + 1) = x² – x⁴.

The area of this slice is

(x² – x⁴) Δ x.

The area of the left piece of R is

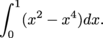
Now for the middle piece, where .

The slice at position x has height

(x⁴ + 1) – (x² + 1) = x⁴ – x².

This means the area of the slice is

(x⁴ – x²) Δ x.

The area of the entire middle piece of R is

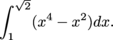
Finally, the right piece, where .

The slice at position x has height

5 – (x² + 1) = 4 – x².

The area of this slice is

(4 – x²) Δ x,

and the area of the right piece of R is

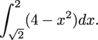
Putting all the integrals together, the area of R is

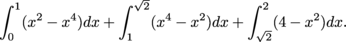
\item With horizontal slices, we need two integrals. The graphs y = x⁴ + 1 and y = x² + 1 cross over each other at the point (1,2). So we need to split R into a lower region where 1 ≤ y ≤ 2 and an upper region where 2 ≤ y ≤ 5.

In the lower region, the length of the slice at height y is

(y – 1)^1/4 – (y – 1)^1/2.

The area of the lower region is

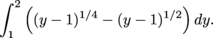
In the upper region, the length of the slice at height y is

(y – 1)^1/2 – (y – 1)^1/4.

The area of the upper region is

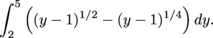
Adding these integrals, we find that the area of R is

Answer

Following the hint, let's find the coordinates of the points. Since we're looking at the unit circle, the point at angle θ has coordinates (cos θ, sin θ).

We can fill in the coordinates of the point at angle  immediately:

To find the angle for the other point, we subtract  from :

,

so the coordinates of the second point are

.

If we're using vertical slices we need to split the region R into two pieces at , because, for , the upper bound of R is a line, and for , the upper bound of R is the circle.

Let's find the area of the left piece of R.

For  the upper bound of R is a line that goes through the origin and has slope

The equation of this line is .

The lower bound of R is the line y = x. This means the height of the slice at location x (for ) is

The area of the slice is

Since x runs from 0 to  in the left piece of R, the area of the left piece of R is

.

Now for the right piece of R.

For  the upper bound of R is the equation of the circle, x² + y² = 1 or

.

The lower bound of R is still the line y = x.

The height of the slice at position x (for ) is

The area of the slice is

Since x runs from  to  in the right piece of R, the area of the right piece of R is

Putting these integrals together, the area of R is