A transversal is a line, or line segment, that intersects two or more other lines, or line segments. When a transversal intersects parallel lines, many angles are congruent. Let's take a peek at what this means. Line segments k and j are parallel. Line segment l is a transversal.

As we mentioned before, when this happens we get a bunch of pairs of congruent angles. Remember: these angles are only congruent when the two lines crossed by the transversal are parallel. These pairs have nifty vocabulary terms to go with them. Here they are:
- Corresponding angles: angles that are in the same position on each line. There are four sets of these angles:
 .
. - Alternate interior angles: angles on opposite sides of the transversal and on the interior of the parallel lines. There are two sets of alternate interior angles:
 .
. - Alternate exterior angles: angles on opposite sides of the transversal and on the exterior of the parallel lines. There are two sets of alternate exterior angles:
 .
.
There are other pairs of angles in a transversal that aren't congruent but they do complete each other like peanut butter completes jelly. These are pairs of supplementary angles, meaning they add up to 180°, and they have their own peachy names. Again, these pairs of angles are only supplementary if the two lines crossed by the transversal are parallel. They are:
- Consecutive exterior angles – angles that are on the same side of the transversal and are both outside the parallel lines. There are two sets of these angles:
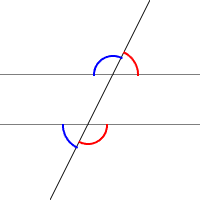
- Consecutive interior angles – angles that are on the same side of the transversal and are both inside the parallel lines. There are two sets of these angles:

Look Out: these pairs of angles are congruent or supplementary only when the transversal cuts parallel lines.
Example 1
Lines i and k are parallel. ∠A = 120°.
|
Example 2
Lines i and k are parallel. ∠A = 120°
|
Example 3
Lines i and k are parallel. ∠A = 120°
|
Example 4
Lines i and k are parallel. ∠A = 120°.
|


 ?
?
 ?
?
