Sketching a Rational Function Examples

Sketch a rough graph of .

Our goals are to find the asymptotes, find the x- and y-intercepts, and then sketch out the graph. For step one, we notice that the degree of the denominator is larger than the numerator. That's a sure sign of a horizontal asymptote at y = 0. We also see that the denominator equals 0 at x = -1, so that's a vertical asymptote.

Plug in 0 for x to get the y-intercept:

That was easy enough. That's (0, 2). The x-intercepts are any points where the numerator equals zero. However, our numerator is 2, so we have no x-intercepts.

We're nervous about trying to sketch this with so few points. Let's snag a few more.

Okay, that's better. To summarize:

At x = negative and positive infinity, the graph approaches y = 0.

There's a vertical asymptote at x = -1. The graph will bend to avoid this line.

We have four points, two to the left of x = -1, two to the right.

Sketch a rough graph of .

This time we have some kind of slant asymptote. Look at the degree of the polynomials: it's 2 over 1.

We have a slant line of y = x – 2. A quick factoring of the top shows that the numerator is equal to (x + 4)(x – 4), which doesn't cancel anything out. That means we also have a vertical asymptote at x = -2.

Now for the intercepts:

(x + 4)(x – 4) = 0

We have intercepts of (0, -8), (-4, 0), and (4, 0). Let's grab one more, to the left of x = -2.

Sticking our slant and vertical asymptotes, and our points, all in a big stew, then mixing vigorously, gets us this:

Sketch a rough graph of .

The degrees of the two polynomials are both 2, so we have a horizontal asymptote. The ratio of the leading coefficients is 1:1, so the asymptote is at the line y = 1.

To find any vertical asymptotes, we need to factor and simplify everything.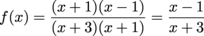

The discontinuity that remains, at x = -3, is a vertical asymptote, while the one that disappeared, x = 1, is a hole.

Next on the agenda is finding the intercepts. For y we have: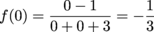

x is next:

x² – 1 = 0

x = -1 and 1

Woop, woop, woop, warning! We already have a hole at x = 1, so disregard that as an intercept.

All of our points so far are to the right of the vertical asymptote. The other side is completely uncharted territory. How about we send some scouts to x = -4 and -5 to get an idea of what it looks like?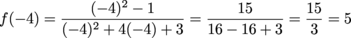

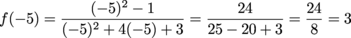
We have the asymptotes, we've seen the points, we know where the holes are; we're ready to rock and roll. And to plot this graph.