Things are going great so far. These limit things are easy, right? Well, we hope so. They not too complicated so far. In fact, they won't get a whole heck of a lot tougher this section either, as we move from evaluating them graphically to evaluating limits by hand.
The only thing we really have to be careful about is keeping track of which method we're using to evaluate these suckers. The first one we'll teach you is called direct substitution. The name really says it all.
Sample Problem
Evaluate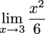 
.
Alllllrighty then. If this were the first section, we would be reaching for our graphing calculator to see what this guy looks like. However, it is actually so much easier than that.
This function is continuous, as there are no x values that make it undefined. As a result, we can put 3 in for x and the outputted value will be our solution.
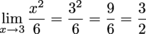
This is great because not only is it easy to remember what to do, but it's actually pretty straightforward as well. Notice that the "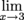
" disappears when we actually substitute 3 in for x. This is typically what's going to happen. We just don't want you to look like a limit noob when you attack these problems.
The direct substitution method is, from now on, our go-to method. It is our A+, number-one choice when it comes to evaluating limits. Why don't we give it another go?
Sample Problem
Evaluate 
.
Direct substitution? Apply directly to the function.
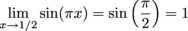
Yes, it really can be that simple. Lucky us.
.
.
.
.
.
.
.
.
.
.
.