The Basics of Rotation

1. What is the angular velocity of the earth as it rotates around its own axis?

2. Measured from space, what is the translational speed of a person standing on the surface of Earth? The radius of the earth is around 6370 km.

3. A carousel spins at a top speed of two full revolutions every minute. Little Bobby gets in line for the carousel and desperately wants to ride the white horse, which he spots π rad away from him (little Bobby knows his radians) when the carousel starts to slow down. In order for the white horse to stop in front of little Bobby, what is the angular acceleration needed by the carousel?

4. How many revolutions does a 66 cm diameter bicycle wheel make as the rider pedals from a stop to 4 m/s in 10 s?

5. What is the tension in each 60 cm string of a bola when the 0.25 kg weights are swung around at 20 rad/s?

Moment of Inertia

1. Which of the following objects, all of mass M, has the highest moment of inertia around a vertical axis through its center of mass?

A)

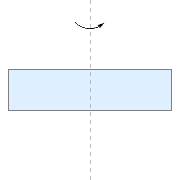
B)

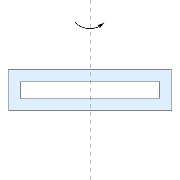
C)

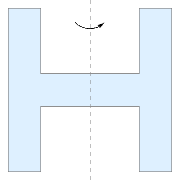
D)

2. Which of the following axes of rotation through the same object of mass M creates the highest moment of inertia?



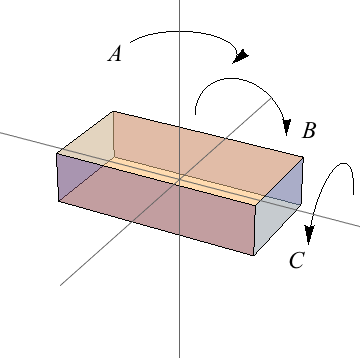
3. What is the moment of inertia of a rod (length L, mass M) spun around its end, instead of the center?

4. What is the moment of inertia of a hoop (radius r, mass M) hanging from a nail in a wall?



5. What is the moment of inertia of a frisbee (approximately disc shaped, weighing 175 g with a 12 cm radius) flying in an arc with a 3 m radius?

Torque

1. Screws and bolts are often rated with a maximum torque they can withstand during tightening before they break. If a screw is rated at 50 N · m and you have a 15 cm wrench, how much force can you use to tighten it?

2. If a sumo wrestler (125 kg) sits 1.5 m away from the fulcrum of a see-saw, how long does the other end of a the see-saw need to be for a gymnast (40 kg) to move the sumo?

3. A tennis player trying to put a lot of topspin on a ball applies a vertical force of 10 N tangent to the tennis ball's surface. If the ball has a 3.4 cm radius and weighs 57 g, what is its angular acceleration after the tennis player's stroke?

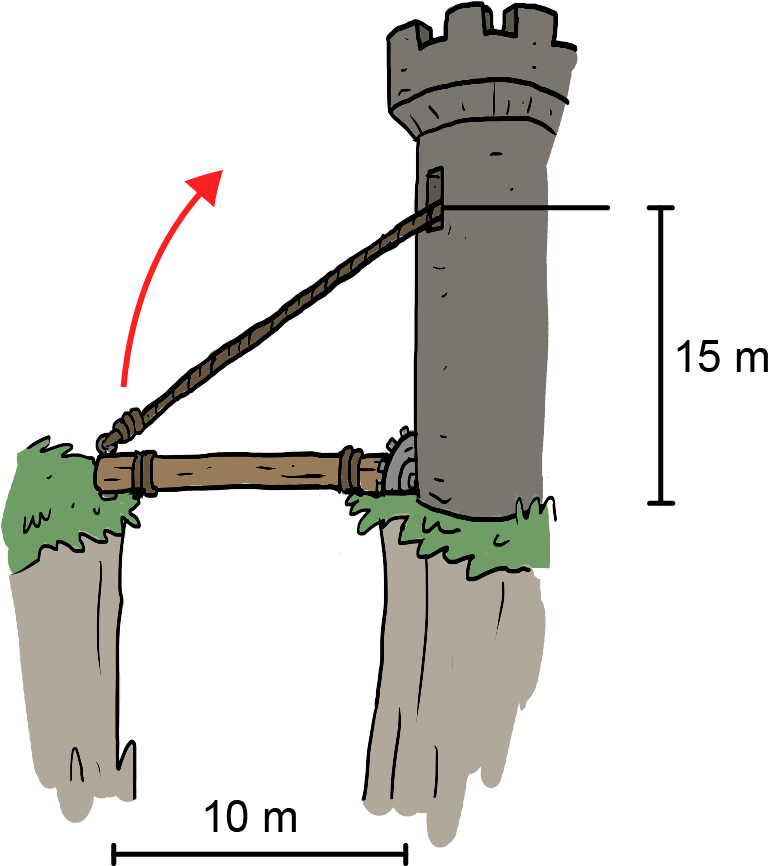
4. The ropes on a 5000 kg drawbridge are attached to the very end of the 10 m long bridge and strung up to the sides of a castle's walls 15 m off the ground. What force must the ropes be pulled on with in order to lift the bridge?



5. How much torque is needed to accelerate a car tire (roughly cylindrical, with a radius of 25 cm and a mass of 10 kg) from a dead stop to 100 rad/s in 6 s?

Angular Momentum

1. What is the angular momentum of a planet of mass M in a circular orbit a distance r away from a star, in terms of its angular velocity ω? What about in terms of its tangential velocity v_t?

2. What is the moment of inertia of a tire swing swaying at 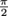rad/s with an angular momentum of 460 kg · m²/s?

3. What is the angular momentum of a 6 kg bowling ball that is 25 cm in diameter as it rolls down a bowling lane? Assume the lane is 18 m long and the ball takes 3 s to make it from the bowler to the pins.

4. When a figure skater spinning at 2π rad/s pulls her arms in and starts spinning at 6π rad/s, what factor has she changed her moment of inertia by? Does it increase or decrease?

5. What is the angular momentum of a hula hoop (0.5 m radius, 0.4 kg mass) rotating around your hips at 2 revolutions per second? The axis of rotation in this case is not the center of the hoop, but the center of your hips—about 22 cm from the rim of the hoop.

Rotation and Energy

1. What is the rotational energy of a frisbee (an approximately 250 g disc with a 10 cm radius) spinning at 30 rad/s?

2. A ball is released from the top of a 5 m hill, rolling down the slope. What is its speed at the bottom of the hill?

3. How much work does our winch do in order to pull the 100 kg weight up a distance of 4 m using a 0.1 m radius pulley?

4. How much work is done by a river when the rushing water increases the rotation rate of a waterwheel from a leisurely 0.2 rev/s to a brisk 1 rev/s? The waterwheel is roughly hoop-like in shape, with a radius of 2 m and a mass of 400 kg.

5. How much power do you need to lift a 50 kg weight at 2 m/s if you can string a rope over a 50 cm diameter pulley?

Answers

The Basics of Rotation

1. What is the angular velocity of the earth as it rotates around its own axis?

The earth spins around on its axis once every 24 hours or so, meaning it completes a full rotation of 2π rad in 86,400 s. Therefore, its angular velocity is .

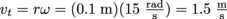2. Measured from space, what is the translational speed of a person standing on the surface of Earth? The radius of the earth is around 6370 km.

A person standing on earth's surface as it rotates around its axis hurtles through space at a terrifying v_t = rω = (6,370,000 m) × (7 × 10^-5 rad/s) = 463 m/s, or around 1000 miles per hour—and this doesn't include the speed of the earth flying around the sun. Buckle up.

3. A carousel spins at a top speed of two full revolutions every minute. Little Bobby gets in line for the carousel and desperately wants to ride the white horse, which he spots π rad away from him (little Bobby knows his radians) when the carousel starts to slow down. In order for the white horse to stop in front of little Bobby, what is the angular acceleration needed by the carousel?

For the white horse to stop in front of Bobby, the carousel must come to a stop after rotating from π rad to 0 rad, Bobby's angle. Rearranging ω² = ω₀²+2αθ gives us an expression for α in terms of the angle traveled and the initial angular velocity (ω = 0 since the final speed is a dead stop): 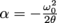, where the negative sign indicates the carousel is slowing down. The carousel's initial angular velocity is 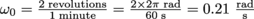, and so the angular acceleration needed to put the white horse by Bobby is 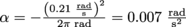. This modest angular acceleration brings the carousel to a halt in .

4. How many revolutions does a 66 cm diameter bicycle wheel make as the rider pedals from a stop to 4 m/s in 10 s?

At 4 m/s, the wheel is rotating at 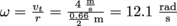. If it takes 10 s for the rider to get up to speed, 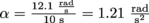. We then have 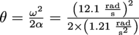. Dividing by 2π, we see this is equivalent to 9.63 revolutions.

5. What is the tension in each 60 cm string of a bola when the 0.25 kg weights are swung around at 20 rad/s?

The tension T in the string is equal to the centripetal force keeping the bola's weight on a circular path. We know 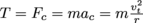, where v_t = rω. Therefore, .

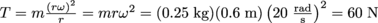Moment of Inertia

1. Which of the following objects, all of mass M, has the highest moment of inertia around a vertical axis through its center of mass?

A)

B)

C)

D)

Pick D—it has the most mass farthest away from the axis of rotation. Remember that since all the objects have the same mass M, any cut out holes will simply move mass further away from the center of mass.

2. Which of the following axes of rotation through the same object of mass M creates the highest moment of inertia?



A, the vertical axis (parallel to the rectangular prism's height). The mass of the prism is, on average, farther from axis A than any other axis because the depth and width of the prism are greater than its height.

3. What is the moment of inertia of a rod (length L, mass M) spun around its end, instead of the center?

I_cm for a rod is 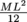. Using the parallel axis theorem with 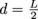gives .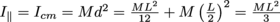

4. What is the moment of inertia of a hoop (radius r, mass M) hanging from a nail in a wall?



The hoop will rotate about the point where it rests on the nail, a distance r away from its center. We then have I_|| = I_cm + Md² = Mr² + Mr² = 2Mr².

5. What is the moment of inertia of a frisbee (approximately disc shaped, weighing 175 g with a 12 cm radius) flying in an arc with a 3 m radius?

The moment of inertia of the frisbee around its center of mass is 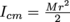. Using the parallel axis theorem, the moment of inertia of the frisbee as it flies through the air is .

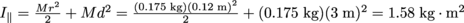Torque

1. Screws and bolts are often rated with a maximum torque they can withstand during tightening before they break. If a screw is rated at 50 N · m and you have a 15 cm wrench, how much force can you use to tighten it?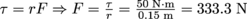



2. If a sumo wrestler (125 kg) sits 1.5 m away from the fulcrum of a see-saw, how long does the other end of a the see-saw need to be for a gymnast (40 kg) to move the sumo?

The gymnast must overcome the sumo's torque of τ = rF = rmg = (1.5 m) × (125 kg) × (9.81 m/s²) = 1839 N · m. To do this, she must sit 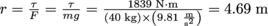away.

3. A tennis player trying to put a lot of topspin on a ball applies a vertical force of 10 N tangent to the tennis ball's surface. If the ball has a 3.4 cm radius and weighs 57 g, what is its angular acceleration after the tennis player's stroke?

τ = Iα, where 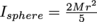. Therefore, .

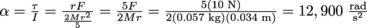4. The ropes on a 5000 kg drawbridge are attached to the very end of the 10 m long bridge and strung up to the sides of a castle's walls 15 m off the ground. What force must the ropes be pulled on with in order to lift the bridge?



To lift the bridge, the castle's defenders have to overcome the torque of the bridge's weight, which tries to rotate the bridge counterclockwise (and is stopped, hopefully, by the bank of the moat opposite the castle). Since weight is a force that always acts from an object's center of mass and the bridge pivots around the end attached to the castle, the lever arm associated with the weight of the bridge is equal to the distance between the bridge's center of mass and the pivot point at the foot of the castle, or 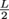. The weight of the bridge creates a torque of 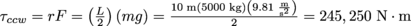. Pulling on the ropes creates force that pulls on the very end of the bridge. This makes a clockwise torque that raises the bridge, equal to τ_cw = rF sin θ, where 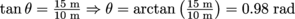. To raise the bridge, we need , or 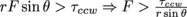. Therefore the minimum force that will start to raise the bridge is .

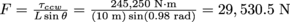5. How much torque is needed to accelerate a car tire (roughly cylindrical, with a radius of 25 cm and a mass of 10 kg) from a dead stop to 100 rad/s in 6 s?

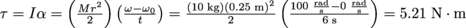
Angular Momentum

1. What is the angular momentum of a planet of mass M in a circular orbit a distance r away from a star, in terms of its angular velocity ω? What about in terms of its tangential velocity v_t?

A point mass moving on a circular path, such as our planet here, has a moment of inertia of 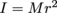. It's angular momentum is therefore 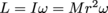. Since 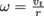, we can rewrite this as 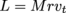. (This formula, in fact, holds for any point mass moving in a circle—and note that .)

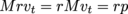2. What is the moment of inertia of a tire swing swaying at 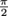rad/s with an angular momentum of 460 kg · m²/s?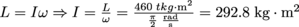



3. What is the angular momentum of a 6 kg bowling ball that is 25 cm in diameter as it rolls down a bowling lane? Assume the lane is 18 m long and the ball takes 3 s to make it from the bowler to the pins.

A spherical bowling ball has a moment of inertia of . It is moving with an angular velocity of 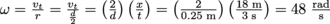. Therefore the bowling ball's angular momentum is .

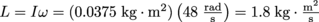4. When a figure skater spinning at 2π rad/s pulls her arms in and starts spinning at 6π rad/s, what factor has she changed her moment of inertia by? Does it increase or decrease?

Since L is constant and equal at both rotation speeds, the threefold increase in angular velocity must be accompanied by a threefold decrease in moment of inertia, as given by the formula L = Iω.

5. What is the angular momentum of a hula hoop (0.5 m radius, 0.4 kg mass) rotating around your hips at 2 revolutions per second? The axis of rotation in this case is not the center of the hoop, but the center of your hips—about 22 cm from the rim of the hoop.

The moment of inertia of a hoop around an axis of rotation through its center is 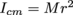, so the moment of inertia of the hoop around your hips is 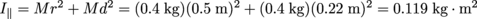. That puts its angular momentum at .

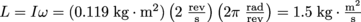Rotation and Energy

1. What is the rotational energy of a frisbee (an approximately 250 g disc with a 10 cm radius) spinning at 30 rad/s?



2. A ball is released from the top of a 5 m hill, rolling down the slope. What is its speed at the bottom of the hill?

Conservation of energy tells us that all of the ball's potential energy will be converted to kinetic energy at the bottom of the hill. However, the ball will have both translational and rotational kinetic energy since it's rolling: 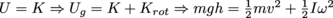. We can solve this for v by first solving for I and ω—for a sphere of mass m and radius r, 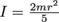and 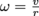. This gives us 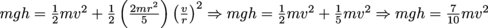. Rearranging, we have .

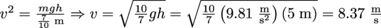(For comparison: a block that slides down a 5 m hill will have a final velocity given by 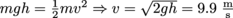. When a ball rolls down a hill, some of the potential energy must be used to spin the ball, which slows the ball's translational speed relative to a sliding block.)

3. How much work does our winch do in order to pull the 100 kg weight up a distance of 4 m using a 0.1 m radius pulley?

The circumference of the pulley is 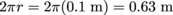, so in order to move the weight 4 m the pulley must rotate through 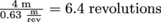, or 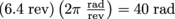. Therefore, the work done by the winch is .

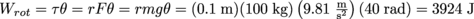This problem can also be solved using translational work: .

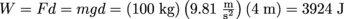4. How much work is done by a river when the rushing water increases the rotation rate of a waterwheel from a leisurely 0.2 rev/s to a brisk 1 rev/s? The waterwheel is roughly hoop-like in shape, with a radius of 2 m and a mass of 400 kg.

The work done is equal to the change in the waterwheel's rotational kinetic energy: .

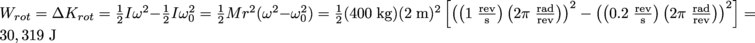5. How much power do you need to lift a 50 kg weight at 2 m/s if you can string a rope over a 50 cm diameter pulley?



To lift the weight, you must use the pulley to overcome a torque of 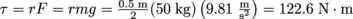. The power needed to supply this torque and raise the weight at 2 m/s is .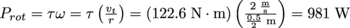