Rotation Terms

Rotation Terms

Angle

Angle measures the rotational displacement of an object from its original location. It depends on a defined axis the object rotates about, but otherwise behaves just like any angle you've encountered in a math class or previous physics chapter—180° is a half turn, 360° is a full turn. 1080° means you're probably Shaun White.

Angular Acceleration

The angular analog of acceleration, angular acceleration measures change in angular velocity. Its units are therefore rad/s2, and it is given by the formula or . A large angular acceleration means an object can change from leisurely revolving to rapidly spinning in a short amount of time—a figure skater going from a large radius turn to a tight, fast spin is a great example of high angular acceleration.

Angular Momentum

Just like objects moving in a line or trajectory have momentum, rotating objects have angular momentum. This is given by the formula L = Iω for large objects with a known moment of inertia (wheels, hula hoops, tops, etc.), or by L = rmvt for point masses a distance r from the center of their circular rotation (a charged particle in a magnetic field, or the earth orbiting the sun). L is in units of kg · m2/s. Once you've mastered angular momentum, you too can join the ranks of the hula-runners.

Angular Velocity

The angular analog of velocity, angular velocity measures change in angle—in other words, the speed of an object's rotation. Its units are rad/s, and it is given by the formula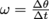 or 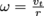. Angular velocity is what we're talking about when we discuss the rpm (revolutions per minute) of an engine, record, hard drive, or a particularly energetic eye roll.

Centripetal Acceleration

When an object moves in a perfect circle, the sum of all the forces on it must equal the object's mass times a specific value called centripetal acceleration. Centripetal acceleration is defined by the formula  and is measured in m/s, just like linear acceleration. Unlike linear acceleration, centripetal acceleration only changes an object's direction, not its velocity—allowing objects moving at a constant speed to follow a circular path. Useful for roller coaster loops; less useful for drag racing.

Centripetal Force

The sum of all the forces on an object moving in a circle is called the centripetal force, given by Fc = mac and measured, like all forces, in newtons. Centripetal force acts to keep an object in its circular path, pulling along the radius of the circle towards the center. It will never change an object's speed, only its direction. No raising X-wings with this one.

Conservation Of Angular Momentum

Like its linear counterpart, the angular momentum of a system is always conserved in the absence of external torques (as opposed to external forces, the prerequisite for conservation of linear momentum). Decreasing an object's moment of inertia will therefore increase its angular velocity according to the formula L = Iω, as figure skaters pulling their arms into their body to increase their spin speed are well familiar with.

Couple / Moment

A couple (sometimes called a moment) is a pure torque applied to an object by means of two equal and opposite forces applied at different points. The net linear acceleration of the object will be zero (by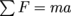 ) but the net angular acceleration, given by 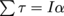will not be zero. Think about that for a moment.

Moment Of Inertia

The larger an object's moment of inertia, the more it resists changes in its angular displacement. This is the analog of mass and displacement in translational motion—a heavy object is hard to push, and an object with a high moment of inertia is hard to spin. Moment of inertia is, essentially, a weighted average of the mass distribution of an object around a given axis of rotation. More mass further away from the axis of rotation makes an object harder to spin, as given by the formula and measured in kg · m2. If you're sitting in a spinning desk chair right now, see it for yourself—hold your arms all the way out and start spinning, then pull them in.

Parallel Axis Theorem

Sometimes an object doesn't rotate around its center of mass, but if we know its moment of inertia around the center of mass it's easy to find the new moment of inertia around the rotation point: I|| = Icm + Md 2. This is the parallel axis theorem, so-called because it only works if the axis of rotation is parallel to the one you used to find Icm or runs through one of Germany, Japan, or Italy.

Radians

The standard measurement of an angle in rotational physics is the radian. A full rotation (360°) is equal to 2π radians (abbreviated "rad"), so 1 rad ≈ 57.296°. Rotational speeds are measured in rad/s, but the radian is ultimately dimensionless. Totally rad, man.

Rolling

An object that is rolling is moving both translationally and rotationally—a bicycle wheel is a good example. As you pedal, the bike (including the wheel) moves forward, and the wheel also rotates. Rolling objects have both translational kinetic energy and rotational kinetic energy, but conservation of total mechanical energy still applies: any increase in rotational speed will, in the absence of outside forces, decrease the translational speed of an object. As the saying goes, a rolling stone gathers no moss because increasing the stone's mass would increase its rotational energy, violating a fundamental principle of the universe.

Rotational Kinetic Energy

The rotational equivalent of kinetic energy—a spinning object has an energy equal to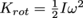 . Pretty convenient how similar that is to , yeah?

Rotational Power

The rotational equivalent of power—to spin an object requires applying a torque τ, and using an amount of power equal to Prot = τω. Power is to rotational power as PowerPoint presentations are to PowerPoint presentations that are printed out, glued to a tire, and rolled down a hill.

Rotational Work

The rotational equivalent of work—it requires an amount of energy equal to Wrot = τθ to spin an object. Don't get too worked up about the difference.

Tangential Motion

When an object moves in a circle, its motion can be described by rotational variables—θ, ω, α, etc.—but further insight can be given by examining its instantaneous linear motion. These variables (vt and at) are called tangential because their direction is always tangential to the circular path the object travels on. Tangential velocities and accelerations are related to rotational velocities and accelerations by vt = rω and at = rα. That means the outside of a spinning object moves faster than the inside. (We'll pause here to let you pick up the shattered pieces of your blown mind).

Torque

A torque is a description of how a force or pair of forces tries to rotate an object. A force F applied a distance r from an object's axis of rotation creates a torque τ = rF, which will try to spin the object around either clockwise or counterclockwise, depending on the direction of F. Torque is measured in N · m. The sum of all torques on a rotating object is given by τ = Iα—the rotational version of Newton's second law, F = ma. Not to be confused with the toque worn by chefs, which only applies force at a distance when there's a small, sentient rat inside.
 Cite This Page

Tired of ads?

Join today and never see them again.
Get Started