For prisms, the fastest way to find the volume is to multiply the area of the base (whatever it is) times the height.
V = Bh
That's all volume is: base times height
Sample Problem
What is the volume of this prism?

Step 1: Find the area of the base. We're talking prisms here, so the bases are always the two parallel congruent shapes. This time around, our base shape is a triangle, so we know that the area equals half the triangle's base times the height. We only know the height of the triangle, though. Hmm, better back up a step.
Step 0: We know the height is 9 centimeters and the hypotenuse is 14 centimeters, but what about the base? Pythagorean Theorem, here we come.
a2 + b2 = c2
(9 cm)2 + b2 = (14 cm)2
b ≈ 10.72 cm
Step 1: Find the area of the base...take two.
B = ½bh
B = ½(10.72 cm)(9 cm)
B ≈ 48.24 cm2
Step 2: Find the volume. In this case, the height is the length of the prism, not the height of the triangle.
V = Bh
V = (48.24 cm2)(12 cm)
Prepare for centimeters cubed.
V ≈ 579 cm3
Awww, yeah.
If we're dealing with a cube, by the way, things get even simpler. All three dimensions of a cube are identical (length, width, and depth). So if we call our cube's side length s, our volume formula becomes:
V = Bh
V = (s2)s
V = s3
Yep, a cube's volume is just the side length cubed. Oh, so that's why raising something to the third power is called "cubing."
To mix up things a little, here's a video on the surface area and volume of a cube:
Example 1
Find the volume of the prism.
|
Example 2
Find the mass of this enormous block of gold if the density of gold is 19.3 grams per cubic centimeter. One meter equals 100 centimeters, and mass is volume times density. |
Exercise 1
Find the volume of the oblique prism in cubic inches.

Exercise 2
How many liters of water will fit into this swimming pool? Assume that 1 cubic foot equals about 28.3 liters.
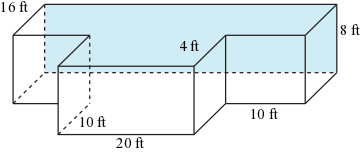
Exercise 3
A regular right pentagonal prism has a perimeter of 10 cm and a height of 8 cm. What's the volume of the prism?




