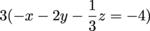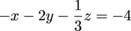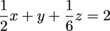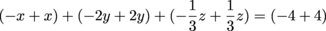Let's start out by tackling x. Multiply the second equation by 3 to cancel with the first equation.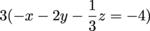 
-3x – 6y – z = -12 Now we add that to 3x + 6y + z = 12: (3x – 3x) + (6y – 6y) + (z – z) = (12 – 12) 0 = 0 We
have an infinite number of solutions here. We can't just wipe our hands
and call it a day, though. Can we learn anything else about the
solutions to this system? Let's try to get rid of x using the second and third equations.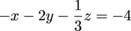 
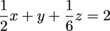
Multiplying the second equation by 2 will do the trick.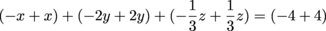 
0 = 0 Okay
then. We've shown that the first and second equations share an infinite
number of points, and the second and third do as well. We could keep
going like this all day, but we don't need to this time. We are
eliminating three variables at a time, every time, because the three
planes are the same. Look again at the original equations: they are
complete multiples of each other. We can say that there are infinitely
many solutions, each one on one of the planes. | 
into one of the original three equations and solve for z. Let's try the first equation.
.
