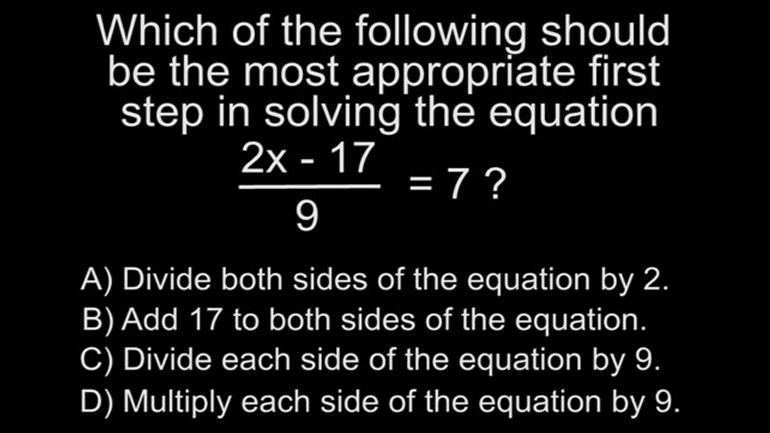ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Word Problems Videos 32 videos
ACT Math: Elementary Algebra Drill 1, Problem 1. What is Ben's current age?
ACT Math: Elementary Algebra Drill 5, Problem 1. How old is Jeremy's brother?
ACT Math: Elementary Algebra Drill 5, Problem 4. How old is Thalia?
CAHSEE Math 3.3 Number Sense 295 Views
Share It!
Description:
Number Sense Drill 3 Problem 3. How much interest will Warren have earned in three years?
Transcript
- 00:03
Here's a shmoopy question for you...
- 00:05
Young Warren Buffet deposited $1,200 into his new bank account. He earns 4% simple interest.
- 00:12
A psychic told him recently he was going to be a rich man someday,
- 00:15
so he's hoping this new bank account will mean, big, big money for him.
- 00:19
Like... maybe even TWO thousand dollars.
Full Transcript
- 00:22
How much interest will he have earned in three years?
- 00:25
Here are the potential answers...
- 00:32
OK so this question is asking about very basic interest calculations...
- 00:36
...in this case we have SIMPLE interest which means that the rate is compounded at the end
- 00:40
of the year and returned to its owner to be spent on... hair growth formula... or whatever.
- 00:45
Simple makes life much... simpler.
- 00:48
So we have 3 iterations we have to do if we want to use the brute force method...
- 00:52
First we take 1200 and multiply it by 1.04
- 00:56
Note the zero in there -- it's 4% interest, not 40
- 00:59
So 1200 times 1.04 gives you 1248.
- 01:03
That's how much is in there after the first year -- 48 bucks in interest income for doing...
- 01:07
a whole lotta nothing.
- 01:09
No wonder the rich get richer.
- 01:11
Since the interest is simple, we just multiply that simple interest number by 3 and we get
- 01:15
3 times 48, or 144.
- 01:18
1200 plus 144 is 1344 and voila -- the answer is C.
- 01:23
But quick gut check for advanced students -- what if the interest had been retained
- 01:26
in the bank account and NOT spent on hair growth formula?
- 01:30
Do the computation again for year 2 and we have 1248 times 1.04 and that gives us 1298, roughly.
- 01:37
Now we do it a third time... 1298 times 1.04 is approximately 1350.
- 01:42
Interestingly, it's a fair $6 BETTER than the simple interest formula -- that
- 01:47
is, by leaving the money in the bank, we made $6 more in interest.
- 01:50
Yeah, it's a latte today, but it adds up.
- 01:53
And if we'd been given this keep-the-money-in-the-bank question to resolve after, say, 27 years of compounding.
- 01:59
...we'd take the entire exam time doing it by this brute force method... so we need
- 02:03
another system -- a simple...ish formula.
- 02:06
We could have gotten the same answer by multiplying the 1200 times the
- 02:10
quantity (1+.04) to the 3rd power.
- 02:14
That is, we'd calculated 1.04 to the 3rd, then multiply
- 02:18
that number by the initial $1200 principal.
- 02:21
Muuuuch easier when many years are involved.
- 02:23
Oh the wealth a whole lot of sitting around on your duff can create.
Related Videos
CAHSEE Math: Algebra and Functions Drill 5, Problem 3. Solve the equation.
We don't like knocking people down to size, but we do like simplifying radicals. Join us?
If fleeing criminals always fled the scene of the crime at perfect right angles, it would be much easier to determine their whereabouts. Fortunatel...
Okay, so this probably isn't going to help you master Pokemon Go, but game theory can be applied to all sorts of situations. Even stomping your old...