Losing your phone is about as much fun having your dentist miss your tooth and drill a hole through your cheek. There’s that moment of heart-stopping panic when you reach for your phone and it’s not there. Panic turns to anger as you realize it's probably your sister who took your phone. She’s always taking things.

Oh man is she going to get it. You march out of your room and turn left down the hallway, because that’s where her room is. After ten minutes of threats and entreaties, you give up on her.

It’s so hard to get the straight story from a drooling two-year-old.

So maybe she didn’t take it, which means your brother must have taken it. Yeah, it sounds like something he would do, just to make you mad. Back down the hallway you go, past your room and on to his room to the right of yours. Banging on his door and yelling gets no response, so you decide to have a look inside. That seems like a good idea right until the point when the suffocating stench of sweaty socks and moldy food hits you.

Yup, it’s probably best to leave that door closed.

You’ve searched left and right, which leaves you back in your room where you started. You walk in sullen and tired, to find your phone peeking out from under an open Algebra text book on your desk. How in the world did it get there? You haven’t studied your Algebra in like...oh right, that exam's tomorrow.

At least you have your phone back so you can tweet about cramming for Algebra. That’s something.

As an added bonus, your phone search was a good example of a post-order tree traversal. Bet you didn't see that coming.

First you visit the left, and then you visit the right, and finally you visit the node itself. (The magic set-up where your room was exactly in the middle between your sister and your brother was the tree and your room was the middle node, in case that’s confusing.)

Let’s see what it looks like in pseudocode:

FUNCTION post_order(node)
	post_order(left_node)	/*run post_order to the left*/
	post_order(right_node)	/*run post_order to the right*/
	IF node:		/*visit the node (if it exists)*/
		visit(node)
	ELSE:			/*if there's no node present,*/
		RETURN
	END IF			/*pull out of the recursion*/ 
				/*by one level*/
END FUNCTION

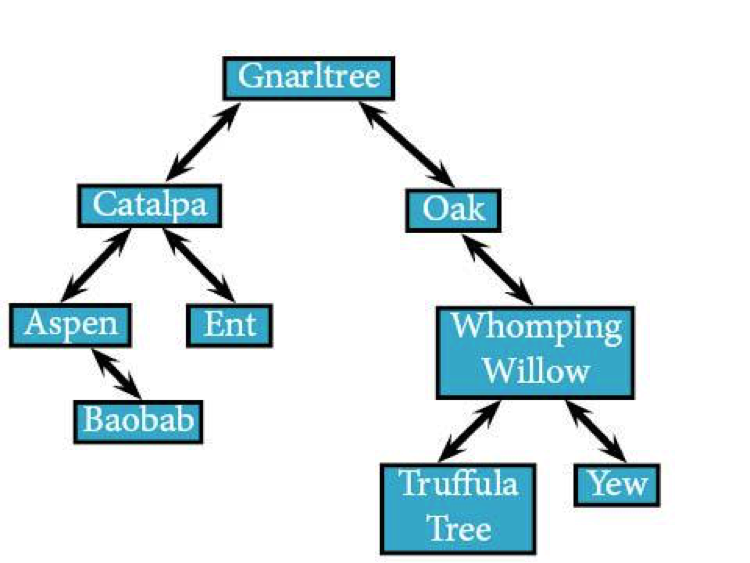
From this traversal, Gnarltree isn't going to be visited until the very end. It's okay. It's the root; it can handle it.

Probably.

 

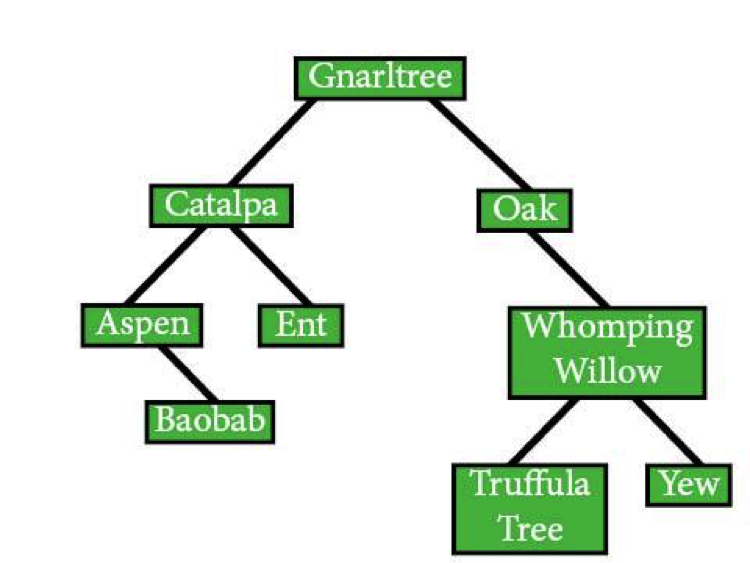
Just like those in-order traversals, we'll travel all the way down from Gnarltree to Catalpa to Aspen without visiting a single node (kind-of rude, but you do you, algorithm). This time, though, we aren't going to visit Aspen before going straight to Baobab. Baobab is going to be the first node we'll visit.

FUNCTION post_order(Gnarltree)
	post_order(Catalpa)
		post_order(Aspen)
			post_order(Baobab)

Once we hit Baobab, there aren't any more children to hit, so we'll visit the middle node. That makdes the algorithm look something like this:

post_order(Baobab)
	IF post_order(NULL):
	ELSE:
		RETURN
	END IF
	IF post_order(NULL):
	ELSE:
		RETURN
	END IF
	IF Baobab:
		visit(Baobab)

 

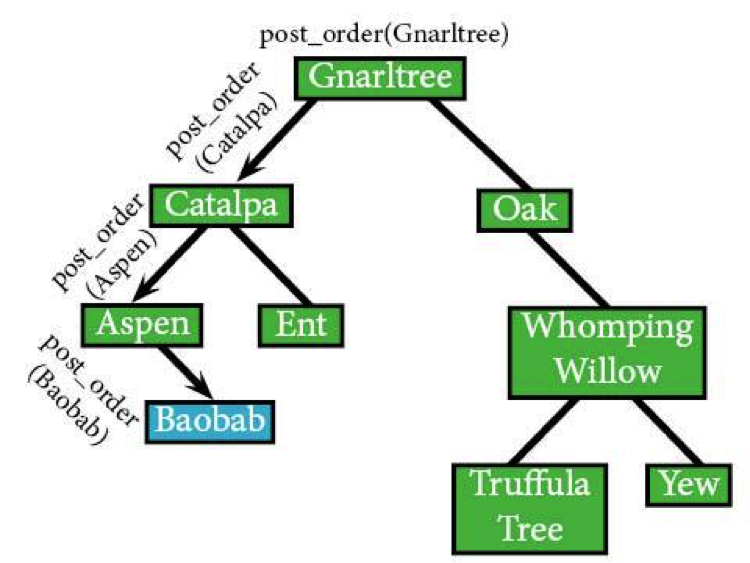
Post_order(Baobab) is now done and visited, so the algorithm returns back to post_order(Aspen) and visit that node.

post_order(Aspen)
	IF post_order(NULL):
	ELSE:
		RETURN
	END IF
	post_order(Baobab)	/*been there, done that*/
	IF Aspen:
		visit(Aspen)

 

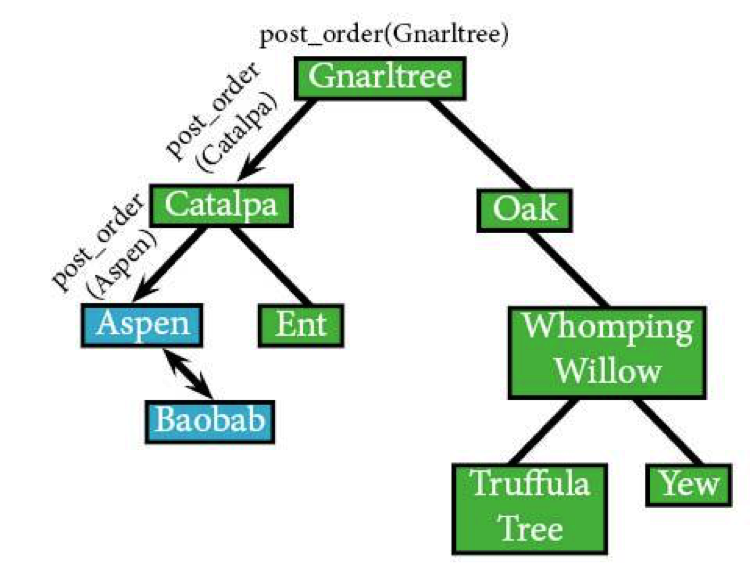
After the visit to post_order(Aspen), the algorithm's going to return to post_order(Catalpa). Before you buy a bouquet of flowers for the visit, keep in mind that the parent of a subtree is actually the thing the algorithm visits last. Since Catalpa still has a right subtree (even if it's just one node), the algorithm has to visit it first. It's time to visit the Ents.

post_order(Catalpa)
	post_order(Aspen) /*been there, done that*/
	post_order(Ent)

Since Ent doesn't have any subtrees, it's the next node to be visited.

post_order(Ent)
	IF post_order(NULL):
	ELSE:
		RETURN
	IF post_order(NULL):
	ELSE
		RETURN
	IF Ent:
		visit(Ent)

 

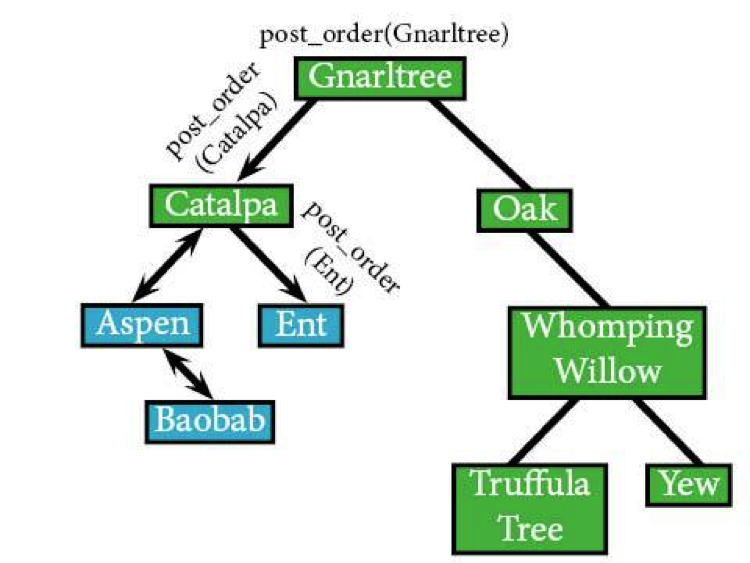
post_order(Ent) returns, bringing us back to post_order(Catalpa), which we can finally visit.

post_order(Catalpa)
	post_order(Aspen) /*been there, done that*/
	post_order(Ent)	  /*this has already returned*/
	IF Catalpa:
		visit(Catalpa)

 

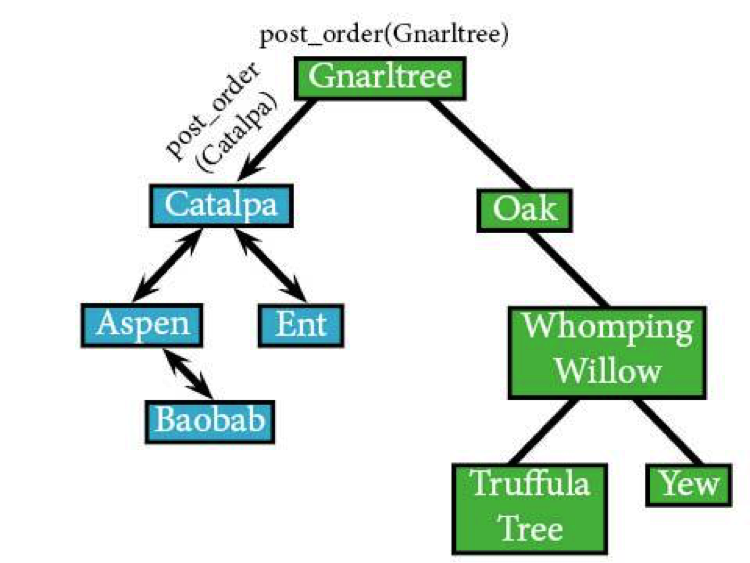
post_order(Catalpa) returns, sending us back to post_order(Gnarltree), which means it's time to head to the right subtree before actually visiting Gnarltree. That means it's on to Oak.

post_order(Gnarltree)
	post_order(Catalpa) /*been there, done that*/ 
	post_order(Oak)

Oak still has subtrees, though, so we have to head down to its subtree before visiting.

post_order(Oak)
	IF post_order(NULL):
	ELSE:
		RETURN
	END IF
	post_order(WW)

 

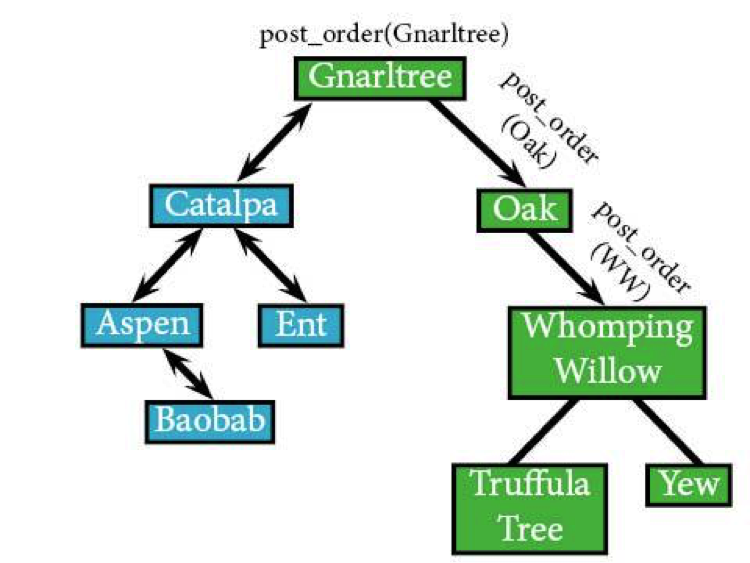
Guess what Whomping Willow has? If you guessed subtrees…you must be paying attention to the binary search tree. post_order(WW) moves on to post_order(TT), that left subtree.

post_order(WW)
	post_order(TT)

Truffula Tree doesn't have any subtrees, meaning it's the next to actually be visited since Catalpa.

post_order(TT)
	IF post_order(NULL):
	ELSE:
		RETURN
	END IF
	IF post_order(NULL):
	ELSE:
		RETURN
	END IF
	IF(TT):
		visit(TT)
	END IF

 

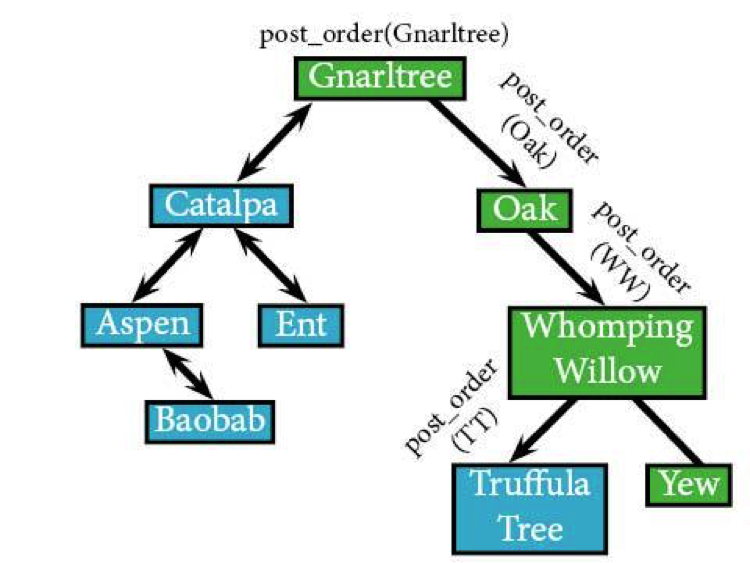
post_order(TT) returns back to post_order(WW), meaning that it's time to hit up the right subtree: Yew.

post_order(WW)
	post_order(TT)	/*We've been there. It was pretty cool.*/
	post_order(Yew)

Yew doesn't have any children—what with being a leaf and all—which means we'll visit it and head right back up to Whomping Willow.

post_order(WW)
	post_order(TT)	/*seen it, bought a souvenir*/ 
	post_order(Yew)	/*souvenirs weren't nearly as cool*/ 
			/*but we saw it*/ 
	IF WW:
		visit(WW)

 

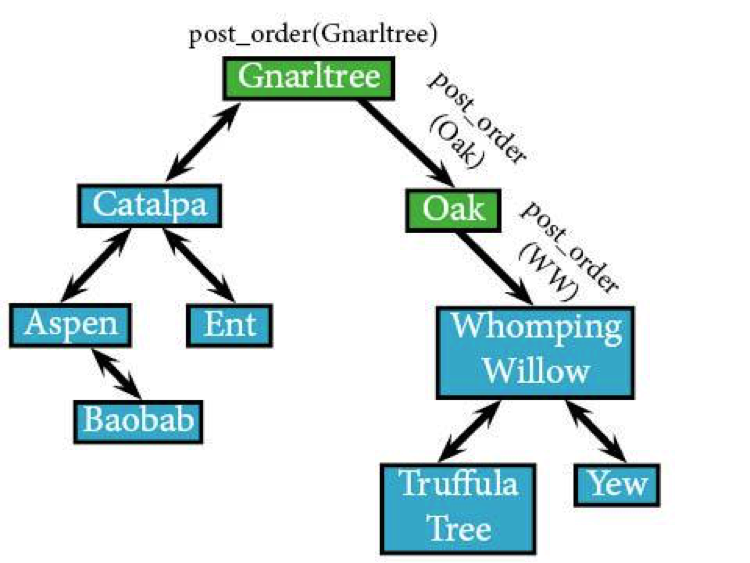
After that we're just retracing our steps, visiting each parent node until we reach Gnarltree. In this case it's Oak and the gnarled root itself.

 

We’re done. It's always a good sign when you end up actually visiting every node in a tree traversal.

The overall order of the trees looks like this:,

Aspen → Ent → Catalpa → Truffula Tree → Yew → Whomping Willow → Oak → Gnarltree.

We visited the root last. You might say it was post-order.

(Source)