If you're looking for something in a tree, you can’t just jump around randomly looking for one specific leaf. That would be ridiculous—not to mention inefficient. You need to have some sort of order when you search.

Enter: the pre-order tree traversal.

There are three main ways (besides a Breadth-First Search) for computer scientists to traverse their trees:

• Pre-order
• In-order
• Post-order

When you actually code these traversals, you can turn them into functions and call them recursively to get the job done.

But first, you need to know how they work.

If you’ve ever braved the scratchy bark and creepy crawly insects that come with tree climbing, you know to start at the base and work your way up. Sure, you could start at the top if you have an airplane or really strong drone to jump from, but it's better for your wall and non-broken limbs to climb up instead. Computer scientists also start from the base (root).

Let’s say we have a tree of trees (how meta), organized so that nodes to the left of a node come alphabetically before the parent node, while nodes to the right are greater (alphabetically). In computer science terms, alphabetical order makes A less than B, while C is greater than B.

In this case, Oak starts with O, which is greater than G, so it goes to the right of Gnarltree (Yoda's favorite tree ). Catalpa starts with C, which is less than G, so it goes to the left of Gnarltree, and…you get the idea.

If you're keeping score, you might notice that this tree is not complete (if it was, it would have every leaf on every level except the final level and all the leaves would be on the left) or full (where every node except the leaves has two nodes), and has a height of 3.

 

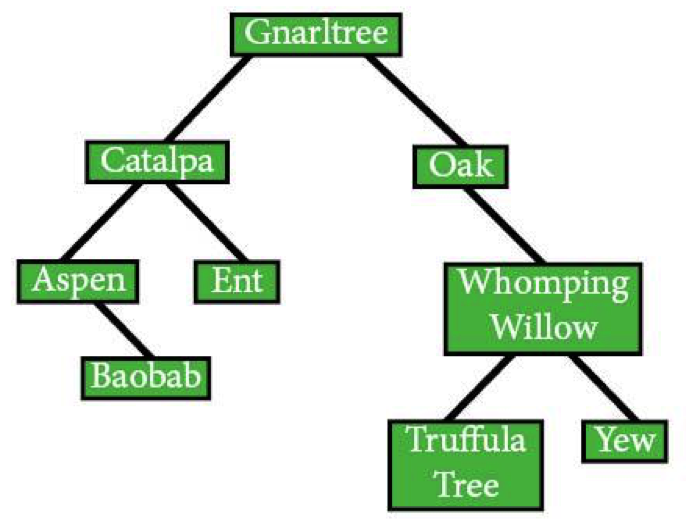
For a pre-order traversal, you'll want to start in the middle, go left as far as possible until you need to go back, then head down the right side.

What?

Say you've got three nodes:

To search in pre-order, you'll look at the middle node, then go immediately to the left one. Once you've looked at that, you'll head back up the middle, look at that node, and then check the right node finally. That's the algorithm. It's pretty simple.

Until you get more than three nodes.

To travel that tree of trees, you'll look at the root, then head all the way down as far left as possible. In pseudocode (algorithms written in language that looks like code but can’t actually run as code without being translated into your favorite programming language), the process would look something like this:

FUNCTION pre_order(node)	/*function pre_order*/
	IF node:		/*visit the node */
				/*(as long as one is there to visit)*/
		visit(node)
	ELSE:			/*if there is no node present,*/
		return
	END IF			/*pull out of the recursion by one level*/
		
	pre_order(left_node)	/*run pre_order on the node to the node’s left*/
	pre_order(right_node)	/*run pre_order on the node to the node’s right*/
END FUNCTION

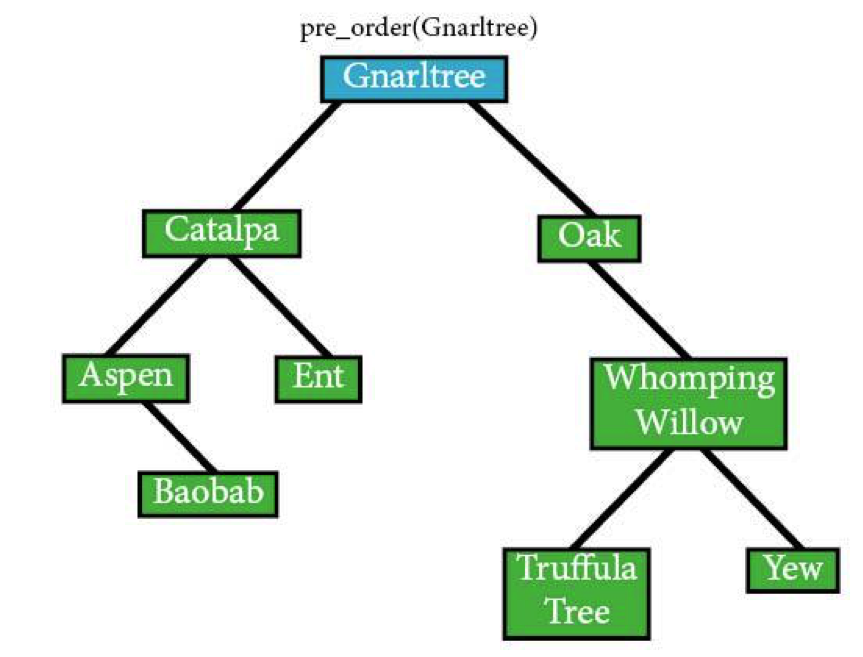
Pre-order traversal of this tree would begin at the root, because that's what the root's for.

pre_order(Gnarltree)
	IF Gnarltree:
		visit(Gnarltree)

 

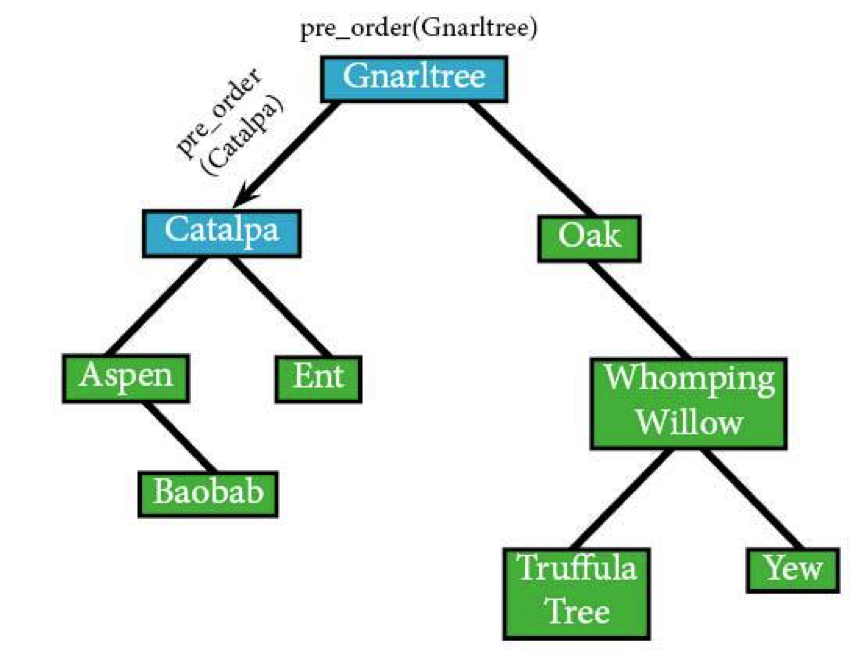
Then pre-order would find Gnarltree’s left node, Catalpa:

pre_order (Catalpa)
	IF Catalpa
		visit(Catalpa)

 

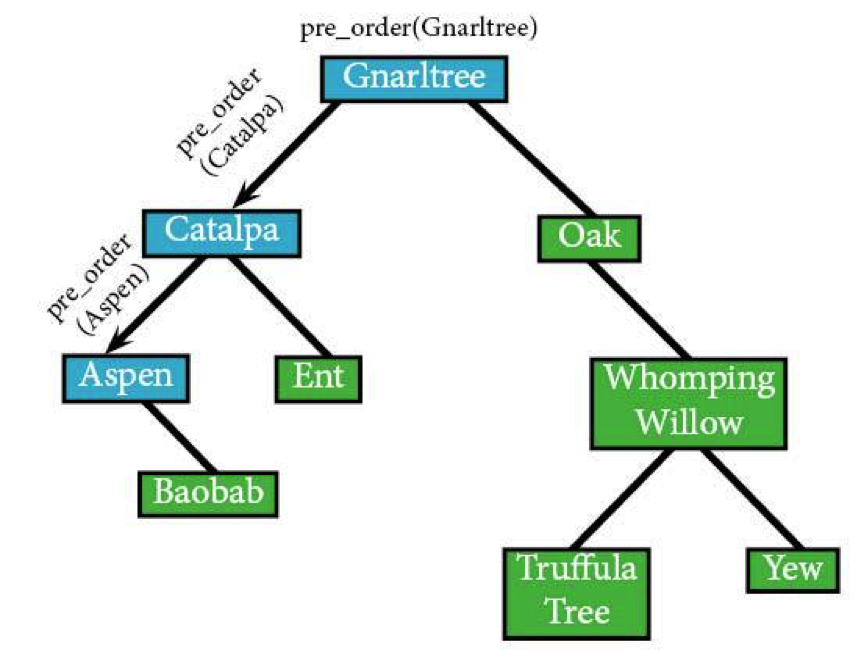
Then it's going to keep moving to the left to find Aspen:

pre_order (Aspen)
	IF (Aspen)
		visit(Aspen)

 

And then Aspen’s left node. Erm…if it existed.

Since it's empty, we're going to get something different from the method.

 

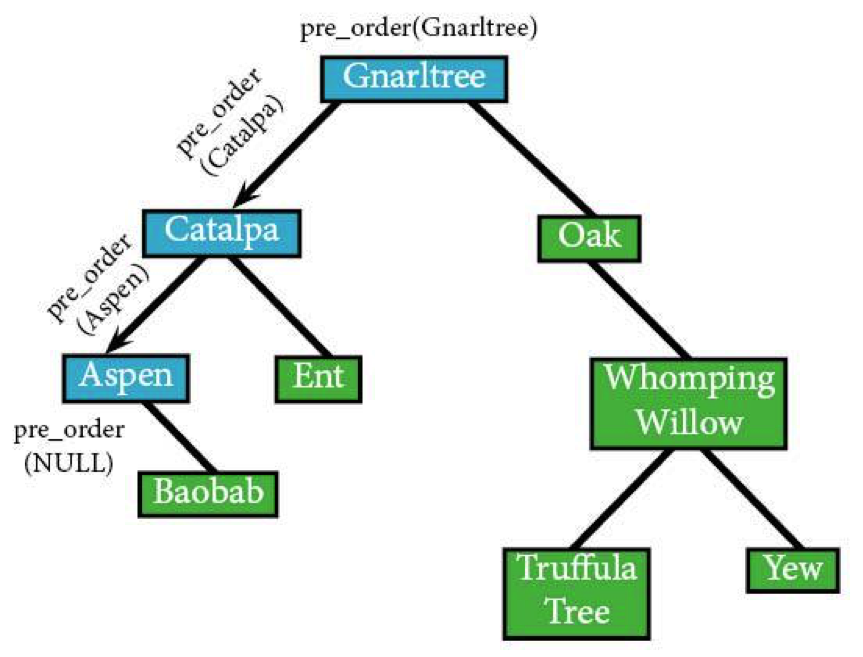
Aspen doesn’t have a left node, making it awfully hard to visit. Instead, the algorithm's going to run everything in the else conditional, making it back up to Aspen.

pre_order (NULL)
	IF NULL:	/*this test fails this time*/
	ELSE:		/*the else block runs instead*/
		RETURN
	END IF

 

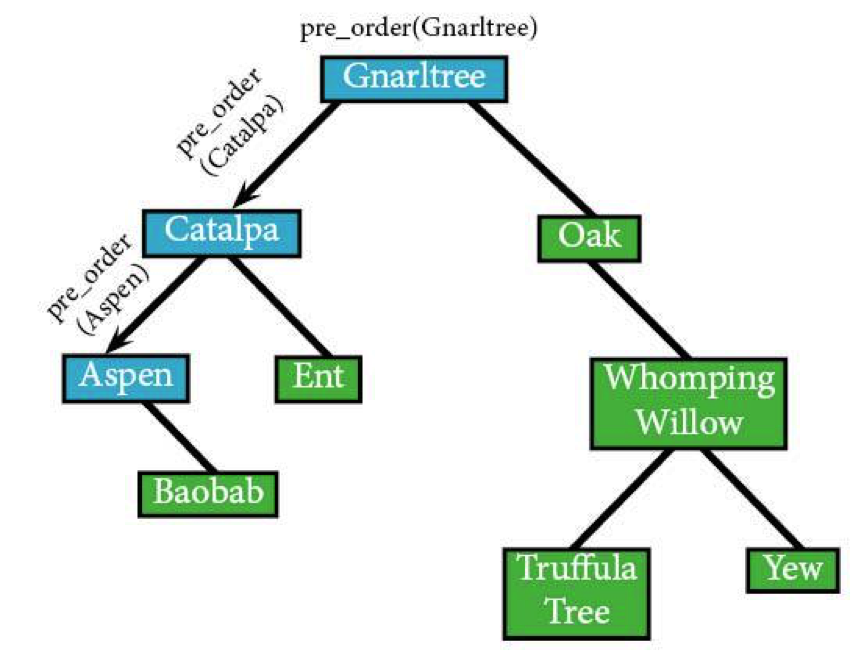
Since the left is done, you'll head to the right: Baobab.

pre_order(Baobab)
	IF Baobab:
		visit(Baobab)

 

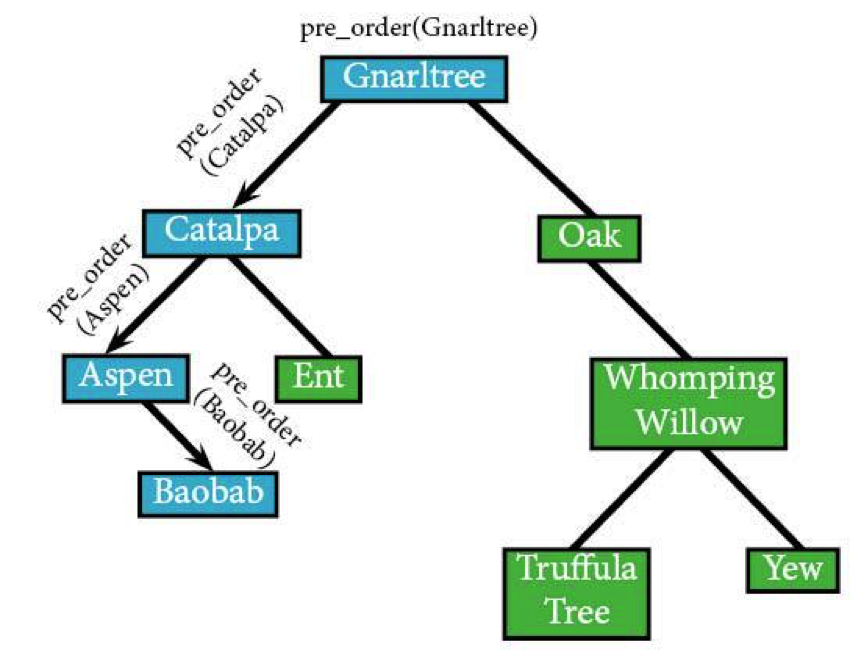
The Baobab, despite representing the circle of life (or something like that) has no children, meaning that the algorithm's going to head straight back up to Aspen.

Baobab's done. There's nothing left to see, meaning we'll never visit it again. The algorithm's going to head up to Aspen without looking back.

 

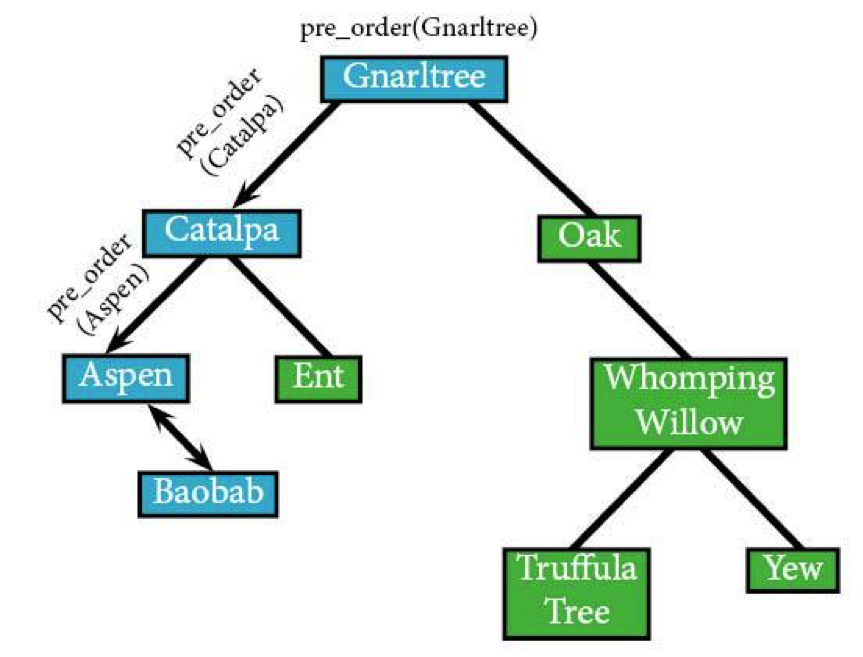
Now pre_order has run on all the nodes to both the left and right of Aspen, which means it's going to pull back up one level to Catalpa. Now that that left subtree's all sorted, it can look at the right subtree.

 

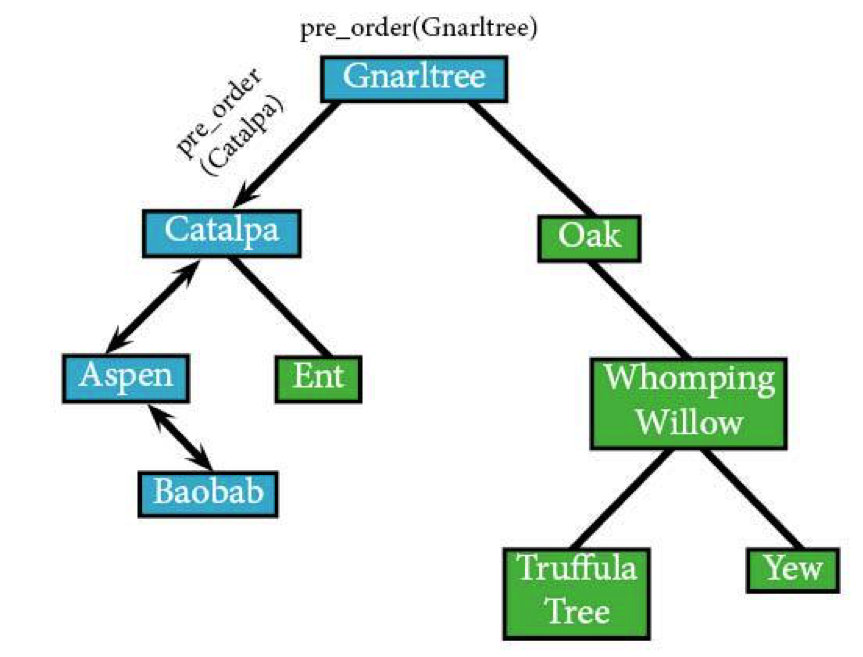
Same thing's going to happen with Aspen. It has no other leads, so it's going to head back up to Catalpa. Since pre_order's now finished on Catalpa’s left node, it'll move on to the right node, Ent.

pre_order(Ent)
	IF Ent:
		visit(Ent)

 

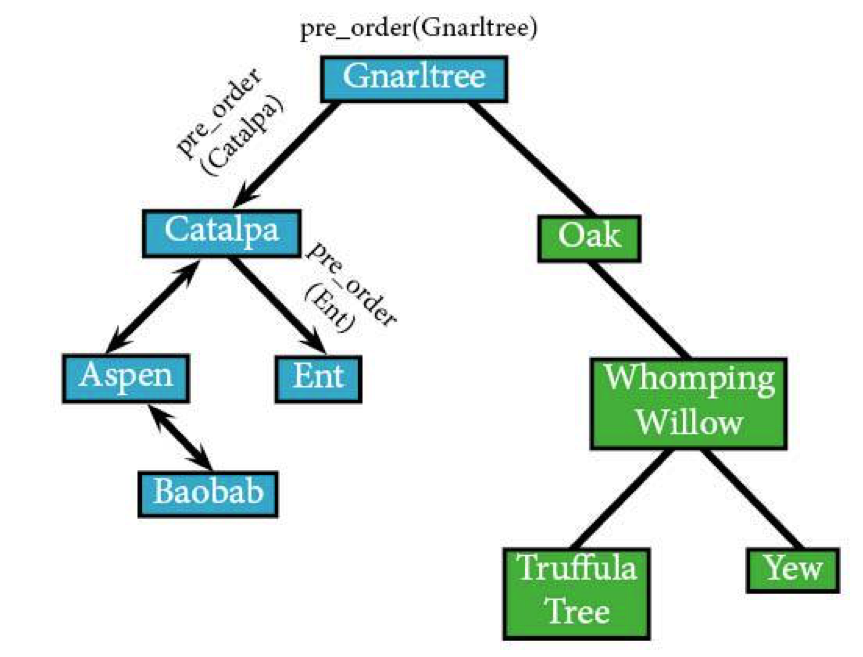
Just like Baobab, Ent has no children (which is actually pretty accurate, when you think about it), so the recursion pulls out another level, back to Catalpa.

 

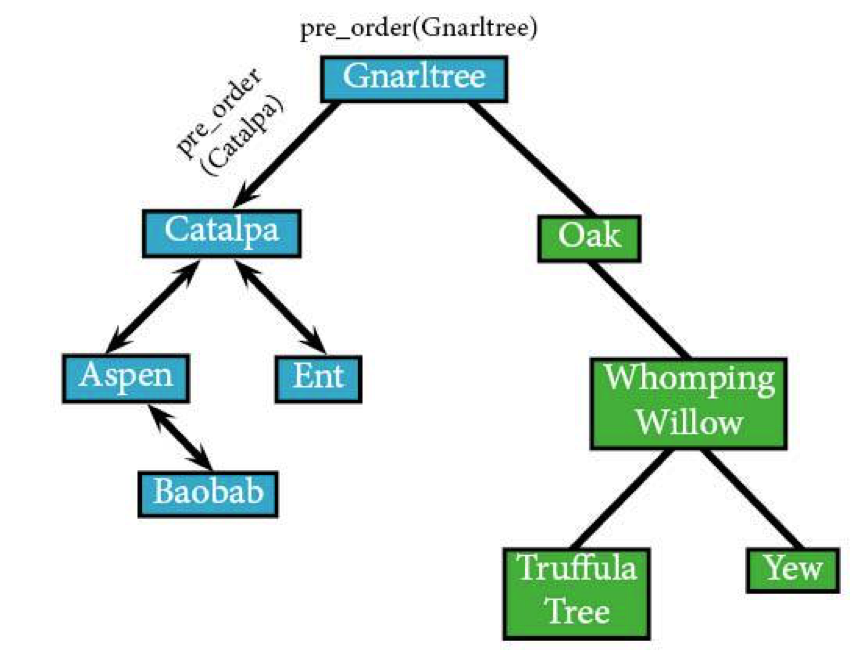
Now that we've seen all of Catalpa's descendants, we'll head back up to the root. It's back to Gnarltree for the algorithm.

 

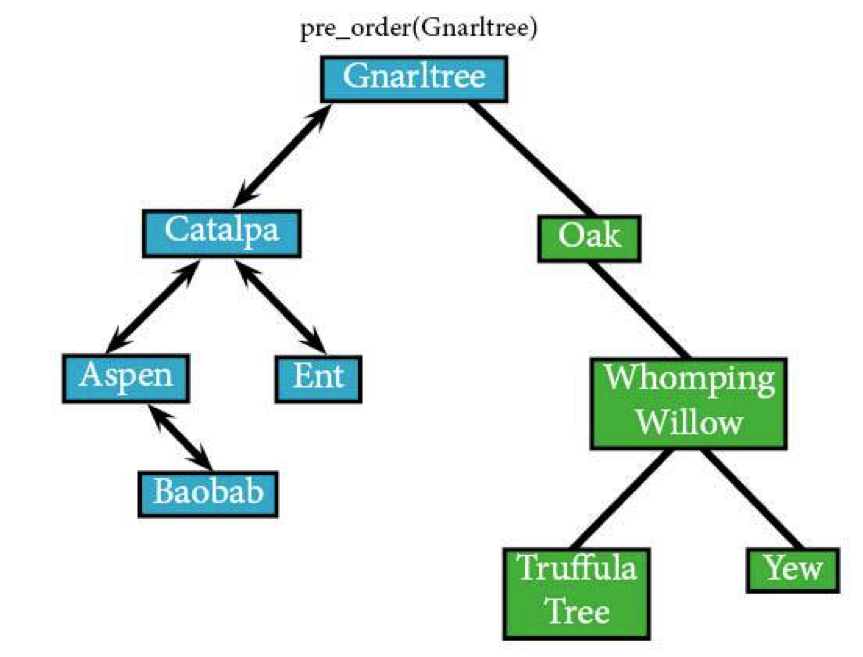
Since we’ve fully explored Gnarltree’s left subtree—that tree within a tree—circled in red, the algorithm can now look at the right subtree boxed in purple.

 

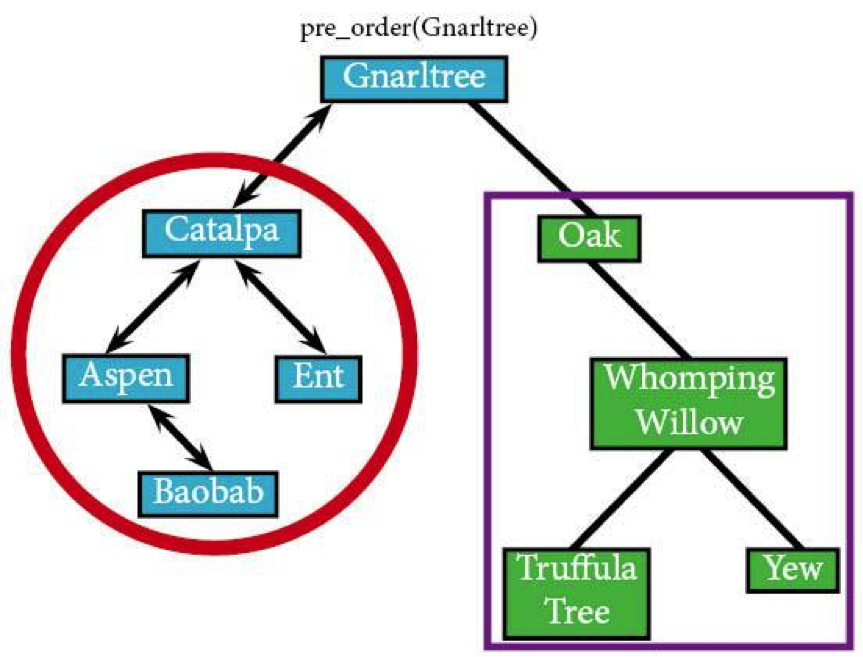
We continue with pre_order(Gnarltree) and go to Oak, Gnarltree’s right node.

pre_order(Oak):
	IF Oak:
		visit(Oak)

 

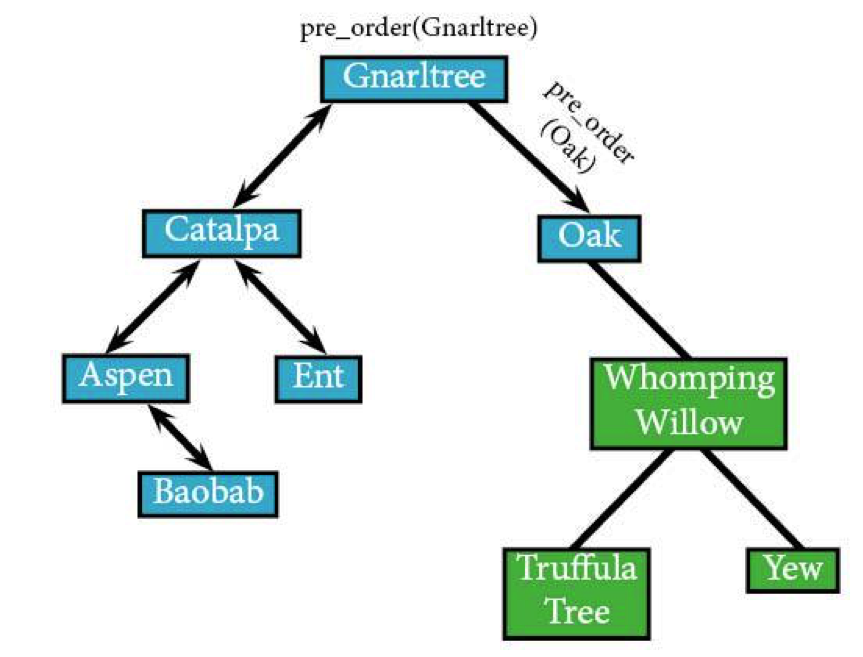
Oak doesn’t have a left node, meaning that we can just skip on over to its right side. The algorithm would technically check it, but…you've got better things to do than spend more time on null values.

Oak's right node, Whomping Willow, is where we go next (abbreved to WW).

pre_order(WW)
	IF WW:
		visit(WW)

 

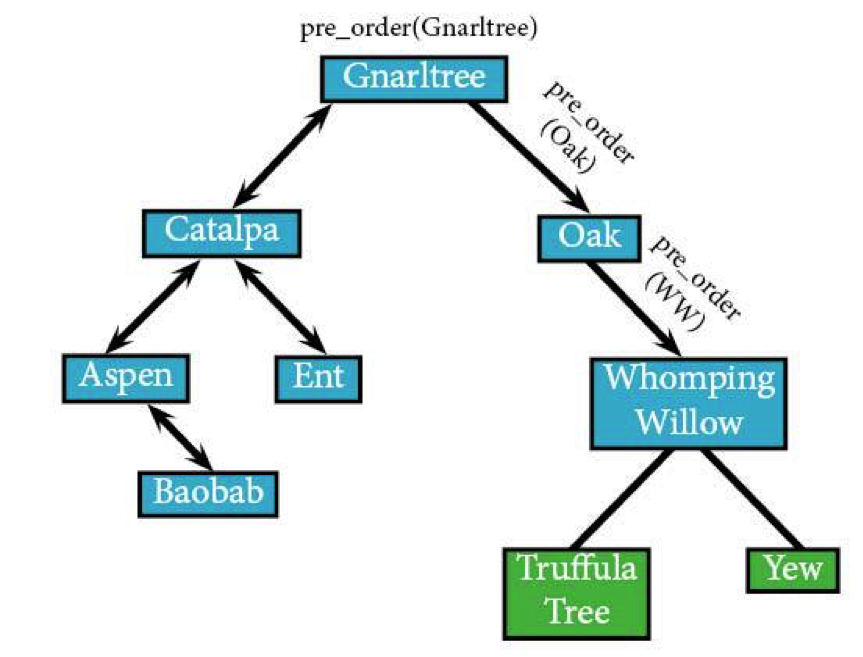
You get the idea. The algorithm's going to head to the left: Truffula Tree (TT).

pre_order(TT):
	IF TT:
		visit(TT)

 

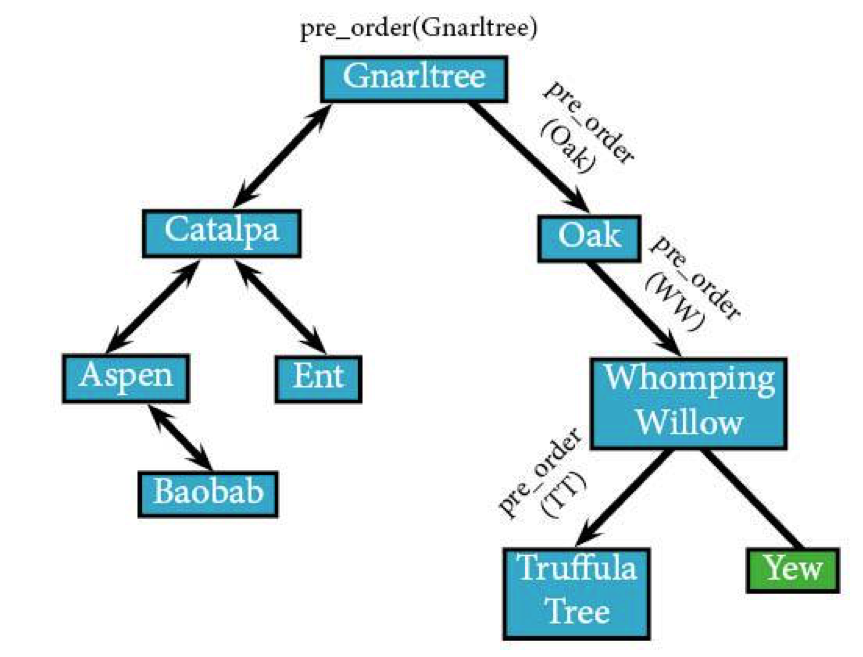
Truffula Tree has no left or right children (which is a totally valid life choice), meaning that the algorithm's going to return back to pre_order(WW).

 

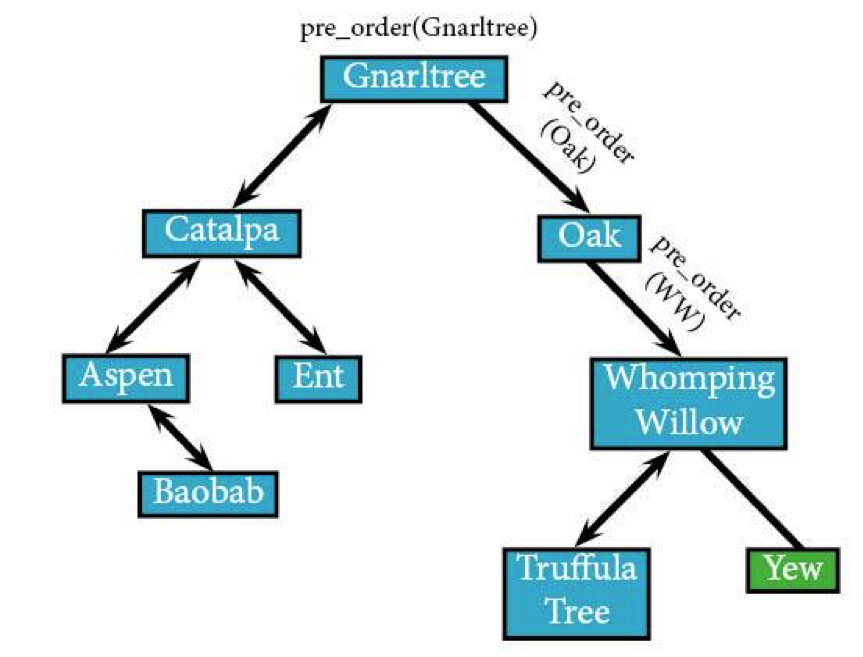
Whomping Willow’s right node (the final unvisited node in the tree) is Yew.

pre_order(Yew):
	IF Yew:
		visit(Yew)

 

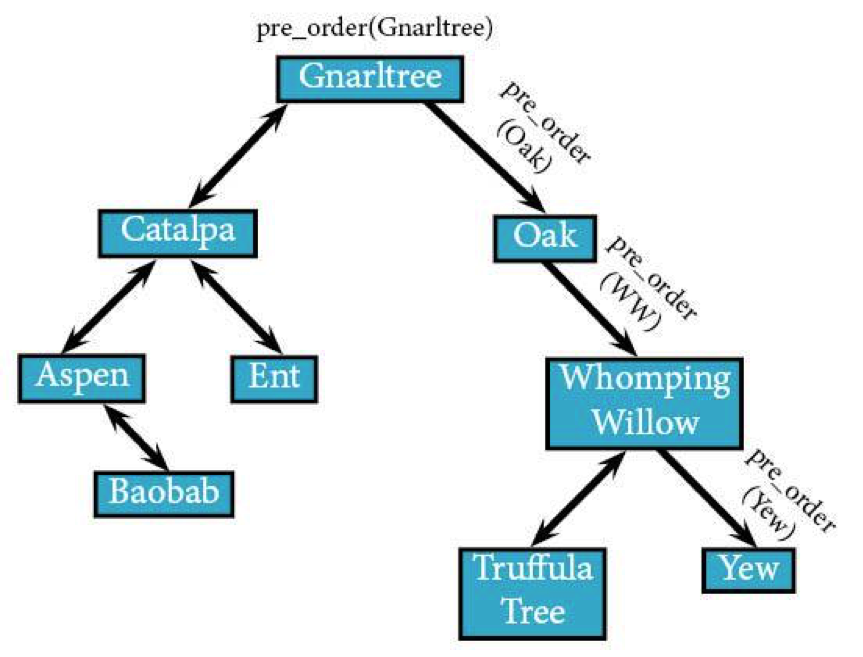
Yew—being the final leaf in the tree—doesn't have any right or left nodes. Since it's the last of its kind, it's going to make the algorithm return back and upwards through the tree to pre_order(Gnarltree), which also returns.

Done.

 

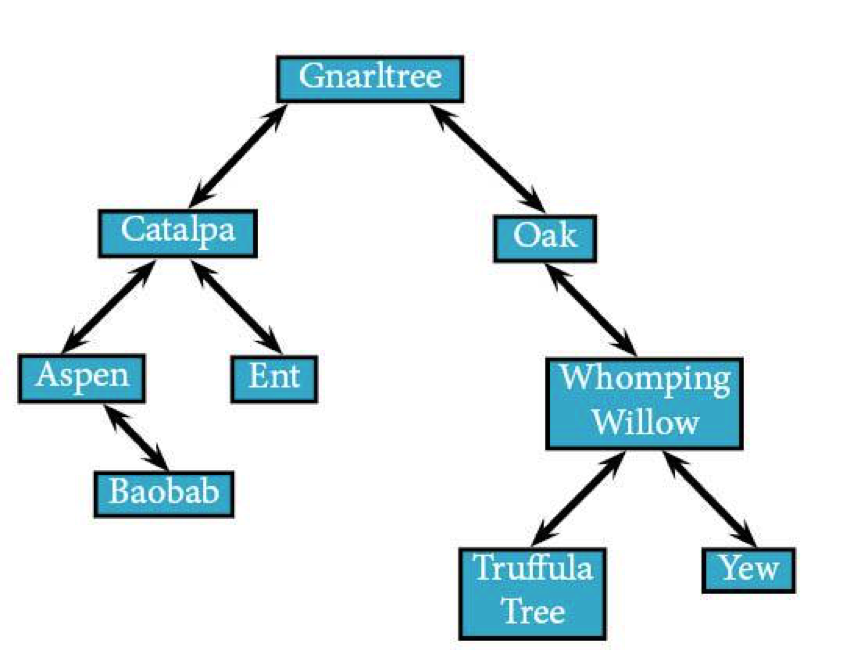
You’ve successfully climbed this tree in pre-order. Good luck making it back down.

Your route through the branches went something like this:

Gnarltree → Catalpa → Aspen → Baobab → Ent → Oak → Whomping Willow → Truffula Tree → Yew.