If we’re taking a nap on a blanket at the park, and a bird poops in the park, what are the chances of the blanket getting hit by the poop? Believe it or not, we can figure that out using probability – geometric probability. In probability, we divide how many desired outcomes there are by how many total outcomes there are. In geometric probability we divide the desired area (desired by the bird that is) by the total area.
Let’s say the park is 50 feet wide and 100 feet long, and we’re sitting on a blanket that is 5 ft wide and 10 ft long.
We can divide the area of the blanket (aka the bird’s target) by the area of the whole park to get the geometric probability. In this case, it’d be 
or 0.01. Then, we can move the decimal two places to the right to convert to a percent, and we get 1%. Looks like we’re safe hanging out there in the park for a while.
What if we bring a blanket that is 40 ft wide and 60 ft long to the same park? First, we’d need a tractor to help us spread it out. Second, the geometric probability of getting bird poop on this blanket increases, a lot. Now the desired area is 40 × 60 = 2400 ft2. The geometric probability has increased to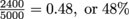 
.
Let’s look at a different scenario. Say the bird was in a wire cage directly above our blanket, positioned so the total area that the bird’s poop can land on is covered by our blanket. What’s the geometric probability that its poop will land on the blanket? The total area is now the exact same as the target area, so the geometric probability is 
meaning there’s a 100% chance it will land on the blanket.
Luckily, a Parks and Rec employee moves the caged bird so it isn’t anywhere near our blanket. What are the chances of getting pooped on by the bird now? Because the target area does not include the blanket, the chances are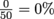 
. Much better odds for a nap in the park.
Example 1
You’re sure you can hit a circle on a target with an exploding watermelon being squeezed by rubber bands, so you’ve set up a square target right in the line of fire with a circle in the center. The square is 5 ft long and 5 ft wide and the circle has a radius of 2 ft. What is the geometric probability of some watermelon landing in the circle? Reminder: the area of a circle is πr2.
|
or 0.5024. Moving the decimal two places to the right and rounding, we get 50.2 %. Now what should we do with the leftover watermelon seeds and target?Example 2
A game is programmed to randomly put your character somewhere on the computer screen that has a rectangular lava pit on it. If you land in the lava pit you lose points. The screen is 10 inches by 17 inches and the lava pit is 2 inches by 10 inches. What is the geometric probability that you’ll land in lava?
|
or 11.8%. May you have better luck than Darth. Example 3
A spit wad machine makes and fires spit wads in a random pattern. What is the probability that a spit wad will hit a 2 ft by 2 ft tile in a ceiling of 50 identical tiles? |
or 2%. 
also equals 0.02 or 2%. Go, fight, spit.