The function f will be discontinuous at any value of c where f(c) is undefined, where  does not exist, or where does not exist, or where  . Think of such values as problem spots. We need to look at the function's definition and find these "problem spots". . Think of such values as problem spots. We need to look at the function's definition and find these "problem spots". Where is f undefined? It looks like x = 2 could be trouble, since then 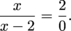 However, when x = 2 we're not using this part of the function's definition. We only use  when x < 0. Since 2 > 1, we have f(2) = 4. when x < 0. Since 2 > 1, we have f(2) = 4. The function f is undefined at  . When . When  we're using the piece of the function definition that says we're using the piece of the function definition that says  so so
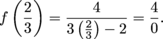 Therefore f is discontinuous at  . . Where can  not exist? not exist? This can happen in between the "pieces". That is, where the function definition changes, or where individual pieces have undefined limits. The only place an individual piece of this function has an undefined limit is at  , which we've already taken care of. , which we've already taken care of. For this function, the function definition changes at 0 and 1. We need to investigate the limit of f as x approaches each of these values. First off, does  exist? For the left-sided limit, we find exist? For the left-sided limit, we find 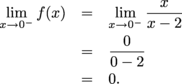
For the right-sided limit, we find 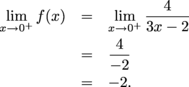
Since the one-sided limits disagree,  does not exist, and f is discontinuous at x = 0. does not exist, and f is discontinuous at x = 0. Does  exist? exist? For the left-sided limit, we find 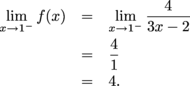
For the right-sided limit, we find 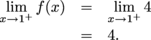
Since the one-sided limits agree, 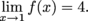 Finally, we need to see if f(c) and  disagree. Again, we only need to inspect those values of c where the function's definition changes over. Since disagree. Again, we only need to inspect those values of c where the function's definition changes over. Since  the function f is continuous at 1. the function f is continuous at 1. We have no more possible trouble spots, f is discontinuous only at  and x = 0. and x = 0. | 
 to see if it exists. As x approaches 1 from the left, we find
to see if it exists. As x approaches 1 from the left, we find 


 , f is continuous at x = 1.
, f is continuous at x = 1.





 does not exist, and the function is not continuous at x = 0.
does not exist, and the function is not continuous at x = 0.
 doesn't exist since
doesn't exist since  .
.
 does not exist, or where
does not exist, or where  . Think of such values as problem spots. We need to look at the function's definition and find these "problem spots".
. Think of such values as problem spots. We need to look at the function's definition and find these "problem spots".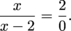
 when x < 0. Since 2 > 1, we have f(2) = 4.
when x < 0. Since 2 > 1, we have f(2) = 4. . When
. When  we're using the piece of the function definition that says
we're using the piece of the function definition that says
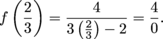
 .
. not exist?
not exist? , which we've already taken care of.
, which we've already taken care of.
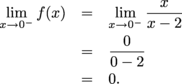
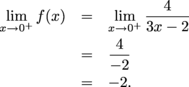
 does not exist, and f is discontinuous at x = 0.
does not exist, and f is discontinuous at x = 0. exist?
exist?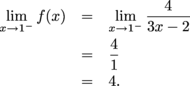
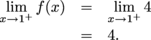
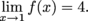
 disagree. Again, we only need to inspect those values of c where the function's definition changes over. Since
disagree. Again, we only need to inspect those values of c where the function's definition changes over. Since  the function f is continuous at 1.
the function f is continuous at 1. and x = 0.
and x = 0.