Can we use the IVT to conclude that f(x) = x3 + 2x + 1 passes through y = 0 on the interval (-2, 2)?
Answer
Yes. For starters, f is continuous on the closed interval [-2, 2]. We have a = -2 and b = 2, so
Since f(a) = -11 < 0 < 13 = f(b), the IVT says that there is some c with -2 < c < 2 and f(c) = 0.
Example 2
Can we use the IVT to conclude that f(x) = expasses through y = 0.1 on the interval (0, 1)?
Answer
No. With a = 0 and b = 1, f(a) = 1 and f(b) = e. The value 0.1 is not between 1 and e, so we can't use the IVT here.
Example 3
Can we use the IVT to conclude that f(x) = sin(x) equals 0.4 at some place in the interval ?
Answer
Yes. f is continuous on the closed interval . With and b = π, we have
and f(b) = sin(π) = 0. Since f(b) = 0 < 0.4 < 1 = f(a), the IVT says there is some c in with f(c) = 0.4.
Example 4
Can we use the IVT to conclude that f(x) = tan(x) equals 0 for some c in (0, π)?
Answer
No. The function tan(x) is not continuous on [0, π] (it has a vertical asymptote on this interval), so we can't use the IVT.
Example 5
Can we use the IVT to conclude that f(x) = x2 passes through 1 on the interval (-1, 1)?
Answer
No. The function f is indeed continuous on the closed interval [-1, 1], but with a = -1 and b = 1,
f(a) = f(b) = 1. The value 1 is not strictly in between 1 and 1 (if we wrote down 1 < 1 < 1 we would be lying), so the IVT won't fly here.
Example 6
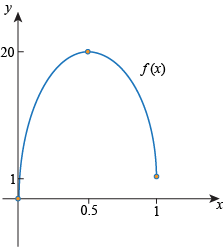
Draw a function that is continuous on [0, 1] with f(0) = 0, f(1) = 1, and f(0.5) = 20.
Answer
There are infinitely many right answers to this. Here's one of them:
We could change the above problem to make f(0.5) equal anything we want.
Be Careful: We can never use the IVT to conclude that a function ffails to hit a value M.
Another thing to be aware of with the IVT is that it doesn't tell us where a function hits a value M, or how many times it does so. On its best day, the IVT can only guarantee we hit the value M at least once.
Example 7
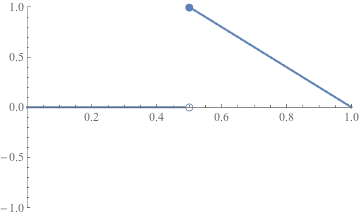
Suppose that f hits every value between y = 0 and y = 1 on the interval [0, 1]. Must f be continuous on that interval?
Answer
No. f could look like this, for example:
This function hits every value from 0 to 1 on the interval [0, 1], but f is discontinuous on this interval.
?
. With 
and b = π, we have
and f(b) = sin(π) = 0. Since f(b) = 0 < 0.4 < 1 = f(a), the IVT says there is some c in 
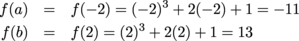
with f(c) = 0.4.
